Zacznijmy od paradoksów matematycznych, pochodzących ze starożytności. Starożytni Grecy (nie było, co dziwne, matematyków rzymskich) dobrze radzili sobie z geometrią, gorzej zaś z arytmetyką.
Problemy z arytmetyką
Pitagoras rzucił hasło ,,wszystko jest liczbą”.Można to interpretować tak: w świecie jest harmonia, wszystkie więc zależności w świecie są wyrażalne przez liczby. Tak zresztą widzi świat współczesna fizyka. Liczby jednak pitagorejczycy pojmowali jako liczby naturalne; dopuszczali tylko ułamki jako proporcje. Ta wizja liczby się załamała, gdy odkryto w szkole pitagorejskiej, że bok kwadratu o długości jeden i jego przekątna nie mają wspólnej miary. I to był paradoks: tak nie powinno być. Dziś mówimy, że \(\sqrt{2}\) jest liczbą niewymierną. Załamała się tu harmonia miedzy geometrią i arytmetyką: nie istnieje wyrażalna przez liczby wspólna miara dla dwóch odcinków. Geometria była jednak bezpieczniejsza. Orzeczono: ,,Liczby zostawmy kupczykom”.
Co do pojęcia liczby, wyjścia były dwa. Pierwsze, to pozostać w sferze mistyki i kontemplować zadziwiające własności liczb. Zwolenników tego poglądu nazwano akuzmatykami (uczniami, słuchaczami). Drugie, to oswoić i lepiej zrozumieć nowe pojęcie liczby. Zwolenników tego poglądu nazwano matematykami, od słowa manthano (gr. μανθάνω) – uczyć się przez zrozumienie. Powtórnego oswojenia dokonali Teajtet (410-368 p.n.e.) przez tzw. ułamki łańcuchowe i Eudoksos (408-355 p.n.e), przez teorię proporcji, wcieloną później do ,,Elementów” Euklidesa. Tak czy owak, Grecy woleli geometrię; jedyny algebraik to Diofantos z Aleksandrii (III wiek), pomawiany zresztą o niegreckie pochodzenie. Takie były konsekwencje odkrycia niewymierności liczby \(\sqrt{2}\).
Prawda matematyki i prawda doświadczenia
Z matematyką mamy kłopot biorący się stąd, że pojęcia matematyczne nie mają oparcia w rzeczywistości. Nie mamy doświadczeń związanych z pojęciem punktu, prostej, płaszczyzny; nie doświadczamy nieskończoności, a pojecie zbioru, podstawowe dla współczesnej matematyki, okazuje się sprzeczne, gdy się z nim obchodzić nieostrożnie. Chyba po prostu nie rozumiemy do końca ani tych pojęć, ani świata matematyki. Zacznijmy od pojęć typu geometrycznego.
Sądzi się powszechnie, że źródłem pojęć geometrycznych jest doświadczenie. Wyobrażenia i intuicje, związane z pojęciem punktu i prostej, oparte na potocznych intuicjach prowadzą jednak do raczej nieoczekiwanych, rzec można – paradoksalnych wniosków. Na przykład, skoro odcinek skład się tylko z punktów, a punkt nie ma długości, to skąd się bierze długość odcinka? Jeśli wprowadzimy pojęcie równoliczności (zbiory \(X\) i \(Y\) są równoliczne, gdy można wzajemnie różnowartościowo przekształcić \(X\) na \(Y\); jest to precyzyjne sformułowanie posiadania przez dwa zbiory identycznej ilości punktów), to się okazuje, że
Twierdzenie. Dowolne dwa odcinki są równoliczne.
Oto dowód. Weźmy odcinki \(AB\) (krótszy) i \(CD\) (dłuższy). Ustawmy je, jak na poniższym rysunku, weźmy punkt 0, wyznaczony przez przecięcie przedłużenia odcinków \(AC\) i \(CD\). Wówczas każdemu punktowi odcinka \(CD\) odpowiada dokładnie jeden punkt odcinka \(AB\) (łączymy punkt z odcinka \(CD\) z punktem \(O\)) i odwrotnie, każdemu punktowi docinka \(AB\) odpowiada dokładnie jeden punkt z \(CD\).
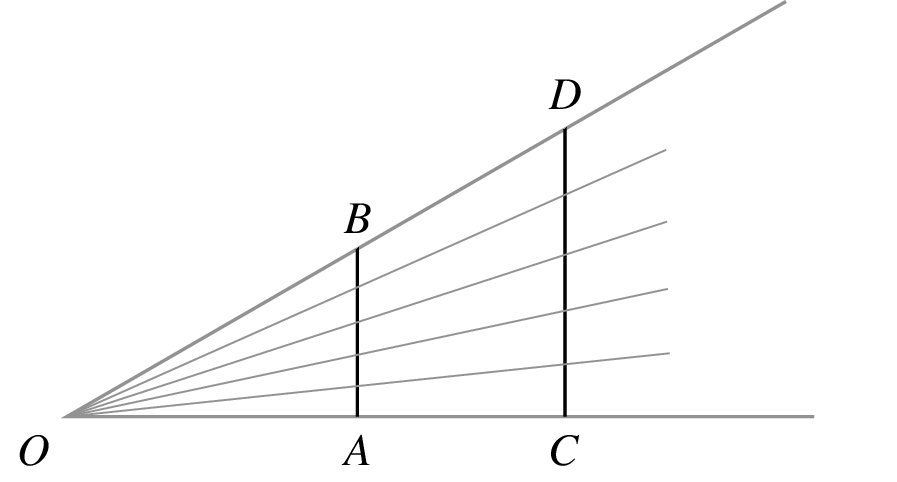
To jednak znaczy, że odcinek długości 1 mm i odcinek długości 1 km mają tyle samo punktów. Czyż to nie jest paradoksalne? Podobny dowód wskazuje, ze równoliczne są dowolne dwa koła i dowolne dwa kwadraty. Można (nieco inaczej, niż wyżej) udowodnić, ze odcinek jest równoliczny z kwadratem i sześcianem i ogólnie – kostką \(n\)-wymiarową dla dowolnego skończonego wymiaru \(n\). Komu mało, niech rozważy następny paradoks, sformułowany przez Arystotelesa.
Weźmy dwa okręgi o wspólnym środku \(A\) i o promieniach \(r\) (mniejszy okrąg) i \(R\) (większy). Niech większe koło toczy się po prostej \(p\). Ustalmy na okręgu o promieniu \(R\) punkt \(C\), będący punktem styczności tego okręgu z prostą \(p\). Po wykonaniu jednego obrotu okrąg ten wyznaczy na prostej \(p\) odcinek o długości \(2 \pi R\); koniec odcinka (punkt \(C’\)) wyznaczony będzie przez punkt \(C\). Połączmy środek \(A\) tych okręgów z punktem \(C\); na odcinku \(AC\) pojawi się punkt \(B\), leżący na mniejszym okręgu. Weźmy teraz prostą \(p’\), równoległą do \(p\), przechodzącą przez punkt \(B\). Kiedy większy okrąg się toczy po prostej \(p\), to mały okrąg się toczy po prostej \(p’\), i zatrzyma się w punkcie \(B’\), gdy zatrzyma się większy okrąg. Odcinek \(CC’\) ma te sama długość, co \(BB’\), czyli \(2\pi R\), ale odcinek \(BB’\) powinien mieć długość \(2\pi r\). Z założenia jednak \(r \neq R\). Z rozważań mamy \(R =r\) więc otrzymujemy sprzeczność.

Wracając do stwierdzenia, że odcinki i kwadraty mają tą samą moc, warto wspomnieć, ze Giuseppe Peano (1858-1932) pokazał w 1890 roku, że można odcinek przekształcić na kwadrat za pomocą przekształcenia ciągłego (skonstruował tzw. krzywą Peany, wypełniającą kwadrat). Ale przecież są to figury o różnych wymiarach. Wobec tego, czym jest wymiar figury?
Nieskończoność nieskończoności
Mnóstwo problemów, czasem zwanych paradoksami, stwarza pojęcie nieskończoności. Nasze intuicje, ukształtowane na obiektach skończonych źle sobie radzą ze zbiorami nieskończonymi. Nawet nie jesteśmy w stanie powiedzieć z całą pewnością, czy w rzeczywistym świecie, w tym momencie są jakieś zbiory aktualnie nieskończone… Jeśli przyjąć podaną wyżej definicję równoliczności, to okaże się, że np. zbiór liczb naturalnych i zbiór liczb parzystych są równoliczne (tzn. liczb naturalnych i parzystych jest tyle samo); niektórzy nazywają to paradoksem Galileusza.
Na podobnej zasadzie oparta jest historia o hotelu Hilberta. Hotel Hilberta ma nieskończenie wiele pokoi, numerowanych liczbami naturalnymi. Do hotelu przybywa następny gość, ale wszystkie miejsca już są zajęte. Recepcjonista radzi sobie z problemem następująco: prosi gościa pokoju nr 1 o przeniesienie się do pokoju nr 2, gościa z trójki o przeniesienie się do czwórki itd. Znów wszystkie miejsca są zajęte, a pokój nr 1 jest wolny. A gdyby przyszło jeszcze \(n\) gości? Nie ma problemu, recepcjonista przesuwa gościa z jedynki do pokoju o numerze \(n+1\), z dwójki do \(n+2\) itd., i znów mamy \(n\) wolnych miejsc dla nowych gości.
Jak więc zdefiniować zbiór nieskończony? Paradoksalną własność, zauważoną przez Galileusza: że zbiór liczb naturalnych może mieć podzbiór właściwy równoliczny ze zbiorem liczb naturalnych (np. zbiór liczb parzystych) Richard Dedekind (1831-1916) uznał za własność odróżniającą zbiory nieskończone od zbiorów skończonych. Zatem: zbiór \(X\) jest zbiorem nieskończonym, gdy ma podzbiór właściwy, równoliczny z samym sobą.
W teorii mnogości wprowadza się pojęcie mocy zbioru: zbiory tej samej mocy to zbiory równoliczne. Wiadomo było, że zbiór liczb naturalnych nie jest równoliczny ze zbiorem liczb rzeczywistych. Georg Cantor (1845-1918) odkrył, że dla każdego zbioru \(X\) istnieje zbiór mocy większej od \(X\); jest to zbiór wszystkich podzbiorów zbioru \(X\). Wynika z tego, że istnieje nieskończona ilość różnych, coraz to większych nieskończoności. Niech Czytelnik zastanowi się nad tym, co znaczy stwierdzenie ,,istnieje nieskończona ilość różnych, coraz to większych nieskończoności”: o jaką ,,nieskończoną ilość” chodzi? Inaczej: czy i jak da się ponumerować kolejne nieskończoności?
Zbiory, zbiory, coraz więcej zbiorów…
Pojęcie zbioru stało się najbardziej podstawowym pojęciem matematyki; świat matematyki opisuje się dziś w języku teorii mnogości (czyli teorii zbiorów). Jeszcze raz podkreślmy, że pojecie to jest pojęciem do opisu matematyki, nie przyrody. Autor tego tekstu nie potrafi np. odróżnić zbioru złożonego z trzech jabłuszek od trzech jabłuszek nie traktowanych jako zbiór (przedszkolaki to podobno potrafią, bo pojęcie zbioru trafiło już do edukacji przed-elementarnej). W przyrodzie zbiory nie występują. I nie ma się temu co dziwić, w przyrodzie też nie występują np. punkty, proste, płaszczyzny i kule.
Nieostrożne posługiwanie się pojęciem zbioru prowadzi do sprzeczności. Najbardziej znany jest paradoks, podany przez Bertranda Russella (1972-1970), zwany po prostu paradoksem Russella. Można go sformułować następująco. Podzielmy wszystkie zbiory na takie, które nie mogą być własnymi elementami, np. zbiór liczb naturalnych nie jest liczbą naturalną (zbiory takie nazwijmy normalnymi) i takie, które mogą być własnymi elementami, np. zbiór wszystkich zbiorów byłby zbiorem, wiec własnym elementem (zbiory takie nazwijmy nienormalnymi). Aby nie komplikować rozważań, przeprowadźmy je symbolicznie. Oznaczmy zbiór wszystkich zbiorów normalnych przez \(\mathfrak{N}\). Formalnie definiujemy go następująco:
\[X \in \mathfrak{N} \iff X \not \in X.\]
Wystarczy teraz spytać, czy zbiór \(\mathfrak{N}\) jest normalny: podstawiając \(\mathfrak{N}\) za \(X\) wprost z definicji mamy
\[\mathfrak{N} \in \mathfrak{N} \iff \mathfrak{N} \not \in \mathfrak{N}.\]
Zatem: zbiór wszystkich zbiorów normalnych jest normalny dokładnie wtedy, gdy nie jest normalny.
Pojecie zbioru normalnego – wyglądające dość naturalnie – prowadzi szybko do sprzeczności.
Samoluby i golibrody
Jeśli nie przemawia do nas ta abstrakcyjna wersja, Bertrand Russell, dobrze władający piórem (został w 1950 r. laureatem nagrody Nobla w dziedzine literatury), oswajał ten paradoks swoim słuchaczom przez przykłady z życia. Oto dwa z takich przykładów. Była sobie ciocia, która wszystkich ludzi dzieliła na samolubów i niesamolubów. Oczywiście lubiła niesamolubów, a nie lubiła samolubów. Rozważmy kwestię: czy sama ciocia jest samolubem czy niesamolubem? Obie odpowiedzi prowadzą do sprzeczności. Jeśli bowiem ciocia jest samolubem, to oczywiście lubi siebie samą, a przecież lubi wyłącznie niesamolubów, przeto jest niesamolubem. Jeśli natomiast ciocia jest niesamolubem, to – ponieważ lubi wszystkich niesamolubów – lubi siebie samą, wobec czego jest samolubem. Zatem: jest samolubem wtedy i tylko wtedy, gdy jest niesamolubem. To był przykład dla pań. Russell podawał też analogiczny przykład dla panów, prosząc o rozważenie sytuacji golibrody z pewnego miasteczka, który – co oczywiste – golił tylko tych, którzy nie golą się sami, a nie golił tych, którzy się sami golą. Z pozoru oczywiste stwierdzenie zaczyna się komplikować, gdy tylko zaczniemy zastanawiać się kto tak naprawdę goli golibrodę… Podobne, jak powyższym przykładzie rozważania wiodą do wniosku, ze golibroda ogoli się sam wtedy i tylko wtedy, gdy się sam nie ogoli.
Z paradoksem Russella i pojęciem zbioru związana jest historia mająca wymiar dramatu. Russell odkrył ten paradoks w 1902 roku, studiując dzieło niemieckiego logika, Gottloba Fregego (1848-1925) Grundgesetze der Arithmetik, rozwijające podstawy logiki i matematyki, oparte m.in. na intuicyjnym pojmowaniu zbioru. O odkrytej sprzeczności zakomunikował Fregemu; paradoksu nie udało się Fregemu wyeliminować, więc jego wieloletni wysiłek był nadaremny. Podstawy okazały się sprzeczne. Dzieła Fregego dziś nikt nie czyta…
Wybory i continua
Podane tu przykłady paradoksów i ,,paradoksów” w matematyce to tylko niektóre, co bardziej proste. Opis innych wymaga większej znajomości matematyki. Różne nieoczekiwane – powiedzieć można, że paradoksalne – konsekwencje posiada jeden z przyjmowanych aksjomatów teorii mnogości, mianowicie aksjomat wyboru (ang. Axiom of Choice). Aksjomat ten głosi, ze dysponując dowolnie dużą rodziną zbiorów \(X\) można wybrać po jednym elemencie z każdego ze zbiorów tworząc tzw. selektor – zbiór zawierający dokładnie jeden element z każdego ze zbiorów rodziny \(X\).
Ostatecznie teorię mnogości zaksjomatyzowano. Najbardziej rozpowszechniona jest wersja podana przez Ernsta Zermelo i Abrahama Fraenkla, zwana aksjomatyką Zermelo-Fraenkla, krótko – ZF. Wersję z aksjomatem wyboru oznacza się przez ZFC. W teorii ZF i ZFC nie da się zrekonstruować paradoksu Russella, ale nie wiadomo, czy czasem aksjomatyka ta nie prowadzi do innej sprzeczności. Wszyscy matematycy wierzą w niesprzeczność teorii mnogości, ale – jak mówiliśmy – świat matematyki i tak jest niesprzeczny; sprzeczny może być tylko jego opis. Warto jeszcze wspomnieć o hipotezie continuum. Mówiliśmy, ze wiadomo, iż zbiór liczb rzeczywistych jest liczniejszy od zbioru liczb naturalnych. Rozważmy pytanie:
Czy istnieje zbiór liczb, liczniejszy od zbioru liczb naturalnych,
ale będący właściwym podzbiorem zbioru liczb rzeczywistych?
Hipoteza continuum głosi, ze taki zbiór nie istnieje.
Odpowiedź na pytanie, czy hipoteza continuum wynika z aksjomatów teorii mnogości $ZF$, w które wierzą1 wszyscy (poza malkontentami) matematycy, okazała się nieoczekiwana, rzec by można – paradoksalna. Po pierwsze, hipoteza continuum jest niesprzeczna z aksjomatami $ZFC$ (wynik ten pochodzi od Kurta Gödla z 1939 roku). Po drugie, niesprzeczna z aksjomatami teorii mnogości $ZF$ okazała się także negacja hipotezy continuum (wynik ten z roku 1973 zawdzięczamy Paulowi Cohenowi). Wynikają z tego dwie ważne konsekwencje.
- Nie da się wyprowadzić (udowodnić) hipotezy continuum z aksjomatów $ZF$;
- Istnieje taki świat matematyki, w którym hipoteza continuum jest prawdziwa, ale istnieje też taki świat, w którym ta hipoteza jest fałszywa;
Więc jaki jest ,,prawdziwy” świat matematyki? Strwożonych pragnę nieco uspokoić: prawdziwość czy fałszywość hipotezy continuum nie ma wpływu na tę część matematyki, z którą ma do czynienia przeciętny matematyk, a nawet matematyk aktywny naukowo. Ale problem pozostaje.
Paradoksy fizyki
Nie tylko matematyka jest pełna paradoksów; na brak nie mogą narzekać także fizycy. Podobnie, jak w matematyce, wejście w tajemnicze, niezbadane regiony, w których nie działają potoczne intuicje dostarcza dużej ilości zaskakujacych stwierdzeń. Kot Schrödingera okazał się żywy i martwy jednocześnie, wyjaśnienie tego fenomenu daje mechanika kwantowa (interpretacja kopenhaska). Badania nad strukturą światła dostarczyły paradoksalnej odpowiedzi, że światło nie ma tylko struktury falowej, ani tylko korpuskularnej, tylko obie równocześnie. Na początku badań nad strukturą mikroświata, tego, gdzie gdzie wzrok nie sięga 2, Werner Heisenberg odkrył w 1927 roku zasadę nieoznaczoności: nie jest możliwy jednoczesny dokładny pomiar położenia cząstki i jej pędu (im lepiej znamy położenia cząstek, tym mniej dokładnie znamy ich odległości, i odwrotnie), a to doskonale utrudnia poznanie mikroświata.
Nie wszystkie jednak pradoksy fizyki wymagają głębszej znajomości tej dyscypliny. Oto przykład. Przyjmijmy, ze obowiązuje zasada względności ruchu: nie da się wykryć ruchu, gdy nie mamy możliwości obserwacji, względem czego się coś porusza. Po drugie, że prędkość światła jest wszędzie taka sama i wynosi 300 000 km/sek.
Załóżmy że zamknięty w rakiecie kosmicznej pędzi kosmonauta, a rakieta właśnie osiągnęła prędkość światła. Kosmonauta postanawia się ogolić. Czy się ogoli? Bierze lusterko i jeśli się w nim zobaczy, to znaczy, ze światło pędzi z prędkością większą, niż 300 000 km/sek, bo prędkości się sumują, a światło idzie od jego twarzy do lusterka. Jeśli się nie zobaczy, to powie: no i pędzimy z prędkością 300 000 km/sek, ale do tego przekonania dojdzie bez wyglądania z rakiety, więc będzie naruszona zasada względności ruchu. No i mamy paradoks. Einstein (bo od niego pochodzi to rozumowanie) zwrócił uwagę na to, że prędkość to iloraz drogi przez czas, więc zajął się pojęciem długości i czasu. Przy dużych prędkościach robią się dziwne rzeczy z długością (to też paradoks).
Komu mało, niech się zainteresuje czarnymi dziurami: tam bez liku znajdzie stwierdzeń godzących w zdrowy, ukształtowany na potocznym poznaniu rozsądek. Na koniec dwa spostrzeżenia dotyczące fizyki. Pierwsze, ze nikt nie wie, dlaczego struktura świata fizycznego jest matematyczna: podręczniki fizyki to w gruncie rzeczy mnóstwo wzorów matematycznych, opisujących zależności w świecie.
Matematyka jest alfabetem, przy pomocy którego Bóg opisał wszechświat – Galileusz.
Jest to jedyny opis, który znajdujemy w fizyce. Dlaczego? Przecież tak być nie musi; kto lubi słowo ,,paradoks”, to może uznać tę własność świata jeśli nie za zadziwającą, to za paradoksalną. Drugie spostrzeżenie. Zmatematyzowane teorie rzeczywistości, podawane przez fizyków, mają związek z rzeczywistością. Królem jest eksperyment i przekonanie, że rzeczywistość ma się tylko na jeden sposób. Zawsze można spytać przyrodę (a mamy ją w jednym tylko egzemplarzu) o to, jak się sprawy mają. Koncepcje, które póki co nie są empirycznie weryfikowalne – a są bowiem i takie – zwane są przez fizyków ,,metafizyką”. Zawsze z sensem można tu pytać ,,Jak jest naprawdę?”.
Takiego kryterium nie ma w matematyce. Być może ,,przyroda matematyczna” jest dana w wielu egzemplarzach: może istnieć matematyka z przyjętą jako założenie hipotezą continuum, jak i matematyka z założoną negacją hipotezy continuum, i czy pytanie: ,,jaka matematyka jest prawdziwa” jest chyba pozbawione sensu, bo co by miało tu znaczyć słowo ,,prawdziwa”?
Uwaga końcowa
Warto dodać, ze matematycy cenią sobie takie nowe twierdzenia, które przynoszą informacje niespodziewane, zwłaszcza ,,paradoksalne”. Towarzystwo matematyków już przywykło do paradoksów i ,,paradoksów”. Nie ma się co temu dziwić, narzędziem czy jak kto woli orężem matematyka jest bowiem jego umysł, a umysł potrzebuje czasem trochę rozrywki. No więc: czy istnieje wyjątek od reguły, a może
nie ma reguły bez wyjątków?
Dodatek o logice
Uważa się, ze logiką, strzegącą poprawności wnioskowań naukowych jest logika klasyczna, nauczana na studiach i w szkołach średnich. Nie znaczy to bynajmniej, nie ma wobec niej wątpliwości. Oto – akceptując logikę klasyczną – musimy zaakceptować prawo Dunsa Szkota, a w konsekwencji za niezawodne uznać wnioskowanie:
| Sokrates biegnie. |
| Sokrates nie biegnie |
|
|
| Jesteś w Rzymie. |
Prawo to mówi, że z pary zdań sprzecznych wynika logicznie dowolne zdanie. Z jednej strony jest to postrach matematyków, bo wynika z niego, że teorie sprzeczne są bezwartościowe, ponieważ zawierają wszystkie zdania w danym języku. Każdemu twierdzeniu będzie w takiej teorii towarzyszyć jego negacja. Dlatego tak dbamy o niesprzeczność matematyki; na założeniu niesprzeczności matematyki oparte są dowody nie wprost.
Z drugiej strony jednak gdyby spytać kogokolwiek nieprzygotowanego, czy podane wnioskowanie jest poprawne, zapewne odpowiedź brzmiałaby, ze nie. Czy wobec tego logika musi akceptować prawo Dunsa Szkota? Okazuje się, że nie musi: istnieją logiki (podlogiki logiki klasycznej), które prawa tego nie zawierają. Są to tzw. logiki relewantne.
Przypisy
- lub zachowują się jakby wierzyli
- czyli świata obiektów mniejszych niż długość fali światła widzialnego
Artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.
