W poprzednich artykułach wyjaśniliśmy pojęcie węzła, splotu ruchów Reidemeistera oraz niezmiennika splotów. Oprócz tego zdefiniowaliśmy indeks przecięcia, który był przykładem niezmiennika splotów oraz użyliśmy go aby pomóc zainteresowanym czytelnikom w rozwiązaniu zagadki z pierwszego artykułu. Celem tego artykułu jest naszkicowanie dowodu poniższego twierdzenia.

Twierdzenie. Indeks zaczepienia jest niezmiennikiem splotów.

W dowodzie użyjemy twierdzenia Reidemeistera, które mówi nam, że aby udowodnić twierdzenie wystarczy sprawdzić zachowanie indeksu zaczepienia na diagramach, które różnią się tylko o jeden z ruchów Reidemeistera. Czytelników, którzy potrzebują powtórki odsyłamy do poprzedniego artykułu.

W pierwszej kolejności zajmijmy się pierwszym ruchem Reidemeistera. Ten ruch dotyczy tylko jednej składowej splotu, zatem skrzyżowanie, które powstaje w ten sposób nie jest uwzględniane w sumie definiującej indeks przecięcia. W konsekwencji pierwszy ruch Reidemeistera nie zmienia indeksu zaczepienia.

Zajmijmy się teraz drugim ruchem Reidemeistera. W rozważaniach pomoże nam poniższy obrazek.

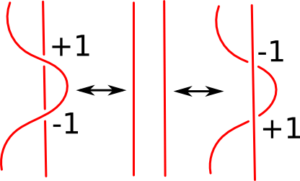
Obrazek przedstawia fragment splotu, przy czym oba widoczne kawałki fragmenty splotu należą do innych składowych. Aby dowód był w pełni poprawny powinniśmy rozważyć aż cztery przypadki w zależności od orientacji składowych splotu występujących na rysunku. Jednak w artykule rozważymy tylko jeden przypadek, pozostawiając pozostałe zainteresowanemu czytelnikowi.

Na powyższym obrazku widać jedną z możliwych sytuacji, którą możemy spotkać w dowodzie. Na rysunku widać, że oba skrzyżowania, które powstają w wyniku zastosowania drugiego ruchu Reidemesitera są skrzyżowaniami o przeciwnych znakach. Zatem ich wkład w sumę definiującą indeks zaczepienia jest zawsze zerowy. W konsekwencji drugi ruch Reidemeistera nie zmienia indeksu zaczepienia.

Na koniec rozpatrzmy trzeci ruch Reidemeistera.

W przypadku trzeciego ruchu Reidemeistera znowu musimy rozważyć kilka przypadków w zależności od orientacji składowych, oraz do której składowej należy każdy ze składników. W artykule rozważymy tylko jeden przypadek, pozostawiając podobne zainteresowanym czytelnikom. Na rysunku widac jedną z możliwych sytuacji, w której każdy widoczny kawałek należy do innej składowej splotu. Na rysunku widać, że lokalna suma przed i po zastosowaniu trzeciego ruchu Reidemeistera jest taka sama i jej skład w indeks zaczepienia jest niezmieniony. Zatem trzeci ruch Reidemeistera nie zmienia indeksu zaczepienia. To kończy dowód twierdzenia.