Weźmy dwa kawałki sznurka długości około metra. Zawiążmy na obu końcach pętelki, na tyle duże, aby zmieściły się w nich nasze nadgarstki. Zaprośmy do pomocy drugą osobę i poprośmy ją, aby wzięła jeden kawałek sznurka i przełożyła dłonie przez pętle na obu końcach sznurka. Teraz weźmy drugi kawałek sznurka, przełóżmy jeden koniec sznurka przez pętle utworzoną przez sznurek i ręce naszego pomocnika, a następnie przełóżmy nasze dłonie przez pętelki na końcach drugiego kawałka sznurka. Zadanie polega na tym, aby rozdzielić dwa kawałki sznurka nie ściągając pętli z naszych nadgarstków.
Zadanie na pierwszy rzut oka może wydawać się niełatwe, jednakże dzięki znajomości pewnych elementarnych faktów z teorii węzłów można sobie ułatwić znalezienie rozwiązania powyższej zagadki.
Teoria węzłów to dziedzina matematyki, która wchodzi w skład topologii. Topologia to część matematyki, która zajmuje się badaniem kształtów. Obiektami zainteresowania teorii węzłów są krzywe zamknięte, zanurzone w trójwymiarowej przestrzeni, które nazywamy węzłami. Fizyczne modele węzłów możemy otrzymać splatając kawałek sznurka i zawiązując jego końce. Najprostszym węzłem jest tzw. węzeł trywialny widoczny poniżej.

Kolejnymi przykładami węzłów są: lewy i prawy trójlistnik oraz węzeł ósemkowy.



Analogicznie możemy zdefiniować sploty, jeżeli zamiast jednego kawałka sznurka użyjemy kilku. Każdy węzeł powstały z jednego kawałka sznurka wchodzący w skład splotu nazywamy składową spójną splotu. Najprostszymi splotami są sploty trywialne widoczne poniżej.


Poniżej przedstawiono kilka innych przykładów splotów: splot Hopfa i pierścienie boromejskie.


Matematycy, którzy zajmują się teorią węzłów, najczęściej nie operują na trójwymiarowych splotach, tylko na ich dwuwymiarowych diagramach. Na wszystkich powyższych obrazkach przedstawiono diagramy węzłów i splotów. Każdy diagram splotu składa się z kilku płaskich krzywych zamkniętych (tzn. krzywych, która nie mają końców), które przecinają się w skończonej ilości punktów. W punktach przecięcia zawsze zaznaczamy który kawałek sznurka idzie górą, a który dołem.
Każdemu splotowi w przestrzeni trójwymiarowej odpowiada wiele diagramów. Gdy dane dwa diagramy różnią się od siebie tak jak obrazki poniżej, wówczas oba diagramy odpowiadają temu samemu splotowi.

Ogólniej, możemy powiedzieć, że ciągłe operacje na diagramach węzłów, które nie zmieniają samoprzecięć, nie zmieniają również typu splotu. Tego typy transformacje nazywamy izotopiami planarnymi.
Kolejny przykład transformacji diagramu, która nie zmienia typu węzła jest przedstawiony poniżej.

Powyższy rysunek pokazuje pewien mały fragment diagramu splotu, który zmieniamy. Reszta pozostaje bez zmian. Taką operację nazywamy pierwszym ruchem Reidemeistera.
Drugi ruch Reidemeistera, przedstawiony poniżej, również nie zmienia typu węzła, któremu odpowiada rozważany diagram.
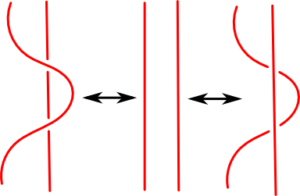
Oprócz powyższych dwóch, wyróżnia się też trzeci ruch Reidemeistera, który posiada dwa warianty.


Postępując dalej w ten sposób można tworzyć kolejne rodzaje ruchów, które nie zmieniają typu splotu reprezentowanego przez diagram. Jednakże nasuwa się pytanie: czy istnieje skończona i zupełna lista ruchów, które można wykonywać na diagramach, które nie zmieniają typu węzła? Przez zupełność mamy na myśli to, że dowolne dwa diagramy przedstawiające ten sam węzeł mogą być przekształcone w siebie przy pomocy ruchów z listy. Odpowiedź na to pytanie podaje twierdzenie Reidemeistera.
Jeśli $D_1$ i $D_2$ są diagramami splotów, które odpowiadają temu samemu splotowi, wówczas istnieje ciąg ruchów Reidemeistera oraz izotopii planarnych przekształcających jeden z diagramów w drugi.
Rozważmy dwa węzły widoczne poniżej.


Na pierwszy rzut oka diagramy wydaję się zupełnie niepodobne. Można jednak pokazać, że oba diagramy odpowiadają ten samemu węzłowi. Poniżej przedstawiono ciąg ruchów Reidemeistera przekształcających jeden diagram w drugi.

W pierwszej kolejności wykonujemy izotopię planarną widoczną powyżej.
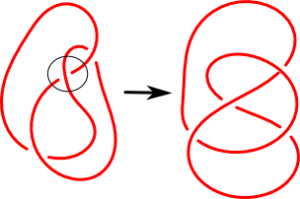
Trzeci ruch Reidemeistera.

Drugi ruch Reidemeistera.

Trzeci ruch Reidemeistera.

Pierwszy ruch Reidemeistera.
W kolejnym artykule pokażemy jak używając twierdzenia Reidemeistera możemy konstruować niezmienniki węzłów, które pozwolą nam rozróżnić niektóre sploty. W dalszej części użyjemy tych niezmienników do rozwiązania zagadki podanej na początku artykułu.
Problemy do przemyslenia.
- Czy istnieją nietrywialne węzły, które posiadają diagramy z jednym punktem samoprzecięcia? A z dwoma?
- Proszę udowodnić, wskazując ciąg ruchów Reidemeistera, że poniższe diagramy odpowiadają jednemu splotowi.


