Trochę historii
W latach czterdziestych dwudziestego wieku matematyk amerykański John von Neumann zastanawiał się, czy dałoby się skonstruować maszynę posiadającą pewne cechy organizmu żywego. Konkretnie, chodziło mu o to, czy maszyna mogłaby skonstruować kopię siebie samej, podobnie jak organizmy żywe mogą się rozmnażać.
Von Neumann skonstruował model matematyczny takiej maszyny. Był to model bardzo skomplikowany, nic więc dziwnego, że inni matematycy zaczęli zastanawiać się, czy można by go uprościć. (Wbrew obiegowej opinii matematycy wolą upraszczać rzeczy niż je komplikować!) I rzeczywiście, jakiś czas później, w 1970 roku, o wiele prostszy model został zaproponowany przez brytyjskiego matematyka Johna H. Conwaya (i wkrótce rozpropagowany przez słynnego popularyzatora matematyki, Martina Gardnera).
Pomysł Conwaya był oparty na koncepcji ,,automatu komórkowego”, badanej po raz pierwszy właśnie przez von Neumanna i Stanisława Ulama, jego pochodzącego z Polski przyjaciela, niecałe trzydzieści lat wcześniej. Aż do tego czasu automaty komórkowe pozostawały dość niszowym pomysłem, znanym jedynie garstce specjalistów. Automaty badane przez von Neumanna były też bardzo skomplikowane. Conway zaproponował bardzo prosty automat komórkowy, który mimo to wykazywał niezwykle złożone i interesujące zachowanie.
Cóż to zatem jest ten automat komórkowy?
Pamiętając, że celem naszego modelu organizmu żywego jest prostota, zapomnijmy o pomysłach rodem z gry Spore (a także o modelach von Neumanna) i wyobraźmy sobie małe żyjątka zamieszkujące pola szachownicy czy kratki papieru. Załóżmy, że w każdej kratce (,,komórce”) może znajdować się jedno takie żyjątko lub może ona być pusta. Nasze żyjątka nie mogą się przemieszczać, a martwe natychmiast ulegają rozkładowi. Innymi słowy, w dowolnej chwili każda kratka może znajdować się w jednym z dwóch stanów: zamieszkała (możemy też powiedzieć: żywa czy ,,włączona”) bądź pusta (martwa, ,,wyłączona”).
Dodatkowo zakładamy, że czas nie biegnie w sposób ciągły, ale że życie kolonii żyjątek toczy się w turach: w chwili \(t=0\) mamy pewien stan, zaś zaraz potem następuje chwila \(t=1\), bez żadnych stadiów pośrednich. (Matematycy powiedzą, że jest to model z czasem dyskretnym.)
Pozostaje jedynie określić, w jakich warunkach żyjątka rodzą się i umierają. Tu zasady są (znów!) całkiem proste. W pustej kratce pojawi się (w następne turze) żyjątko, gdy z kratką tą sąsiadują dokładnie trzy inne. (Umawiamy się, że ,,sąsiadowanie” oznacza kratkę mającą z daną kratką wspólny bok lub wierzchołek, innymi słowy, każda kratka ma osiem sąsiednich). Żyjątko ginie, gdy ma mniej niż dwóch lub więcej niż trzech sąsiadów.
Jak widać, zasady ,,gry” są bardzo proste — aż za proste, chciałoby się powiedzieć, jeżeli mają odzwierciedlać złożone zjawisko życia. Okazuje się jednak, że nawet tak proste zasady prowadzą do zaskakująco złożonych zachowań.
Zanim zaczniemy analizować te zachowania, zauważmy, że nic nie stoi na przeszkodzie, abyśmy te reguły modyfikowali. Nie będziemy się w tym tekście zajmować wariantami gry w życie, ale nadmieńmy, że różne jej modyfikacje to właśnie wspomniane automaty komórkowe. Możemy zatem zmieniać zasady narodzin i śmierci ,,komórek”. Możemy umówić się, że każda komórka może być w jednym z trzech lub więcej stanów (na przykład, nie tylko ,,martwa” lub ,,żywa”, ale ,,martwa”, ,,młoda” i ,,stara”) — oryginalny model von Neumanna zakładał istnienie prawie trzydziestu stanów! Możemy zmieniać zasady ,,sąsiedztwa” (umawiając się na przykład, że ,,sąsiednie” komórki to tylko te cztery, które mają z daną komórką tylko wspólny bok). Możemy rozpatrywać struktury jedno- bądź więcejwymiarowe, a nie tylko płaskie. Okazuje się, że automaty komórkowe mogą posłużyć do modelowania rozmaitych zjawisk, jak na przykład układy elektryczne czy korki na autostradzie.
Klasyczne układy
Zanim zobaczymy ,,ciekawszy” układ komórek, przyjrzyjmy się kilku klasycznym układom o różnych zachowaniach.
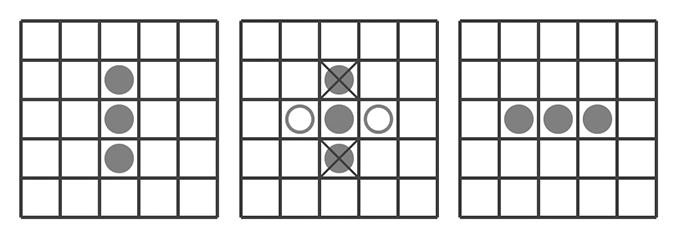
Jednym z prostszych układów komórek, które mają interesujące własności, jest ,,migacz”, składający się z trzech żywych komórek jedna pod drugą.
Jak nietrudno zauważyć, dwie komórki na końcach (skreślone) zginą w kolejnej turze, zaś w miejscach oznaczonych białymi kółkami dwie komórki pojawią się w kolejnej turze. Ponieważ ,,nowy” układ jest identyczny z poprzednim (tylko obrócony o \(90^\circ\)), w kolejnej turze jego ewolucja będzie wyglądała podobnie i całość powróci do stanu początkowego. ,,Migacz” jest zatem jednym z najprostszych oscylatorów, mającym okres dwa (co dwie tury cykl się powtarza). Oscylatorów w Życiu jest więcej — i to o różnych okresach. (Nie znaleziono dotąd m.in. oscylatorów o okresach \(19\), \(23\), \(38\) i \(41\). Udowodniono natomiast, że można skonstruować oscylatory o każdym okresie większym od \(42\).)
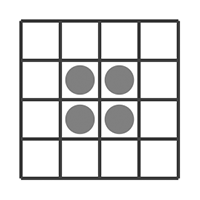
Inną kategorią układów są martwe natury, które można by nazwać ,,oscylatorami o okresie jeden”. Są to układy, w których ani jedna komórka nie ginie ani się nie rodzi. Najprostszą martwą naturą jest blok.
Rodzajów układów w Życiu jest wiele, ale w tym krótkim artykule interesuje nas jeszcze tylko jeden z nich.
Statki kosmiczne
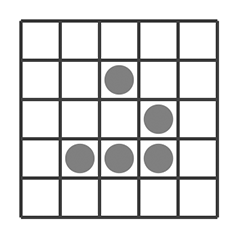
Oczywiście, martwe natury wydają się niezbyt interesujące, a oglądanie oscylatorów z czasem może się znudzić. Okazuje się jednak, że w Życiu istnieją układy o innych ciekawych właściwościach. Jednym z najsłynniejszych jest szybowiec.
Okazuje się, że po czterech turach układ wraca do stanu takiego jak początkowy, ale przesuniętego (o jedną komórkę w ,,prawo i dół”). Innymi słowy, szybowiec przemieszcza się po płaszczyźnie z prędkością jednej kratki w prawo i w dół na cztery tury. Istnienie szybowca odkryto bardzo wcześnie, bo już w 1970 roku. Układy komórek, które ,,przesuwają się” w podobny sposób nazwano ,,statkami kosmicznymi” (pomińmy tu drobny problem terminologiczny związany z tym, że szybowiec poradziłby sobie raczej kiepsko w przestrzeni kosmicznej). Okazuje się, że statków kosmicznych jest więcej. Istnieją również ,,działa”, czyli układy, które co jakiś czas ,,produkują” statek kosmiczny. Najbardziej znanym działem jest ,,działo szybowcowe Gospera”, strzelające szybowcami co 30 tur.
Kultura Życia
Mimo, że Życie na pierwszy rzut oka nie wydaje się mieć poważnych zastosowań, prowadzi się cały czas intensywne badania nad układami w tej ,,grze”. Wytworzyła się nawet wokół niej cała społeczność, stosująca swoistą terminologię i poszukująca różnych interesujących układów czy ich własności. Przykładowo, poszukuje się statków kosmicznych o różnych prędkościach. (Szybowiec ma prędkość \(c/4\), czyli czterokrotnie mniejszą od teoretycznie największej możliwej w Życiu. Tę maksymalną prędkość, przez analogię do fizyki, oznacza się literą \(c\) i nazywa prędkością światła.) Poszukuje się sposobów na konstruowanie złożonych układów z prostszych — przykładowo, nasyłając na siebie osiem odpowiednio umiejscowionych szybowców można wytworzyć działo Gospera (technikę tę nazywa się syntezą szybowcową). Mimo, że Życie jest znane od prawie pięćdziesięciu lat, cały czas odkrywa się nowe — niekiedy zaskakujące — układy. (Przykładowo, społeczność Życia z wielkim zaskoczeniem i poruszeniem zareagowała na odkrycie w 2016 roku statku kosmicznego poruszającego się równolegle do linii siatki z niespotykaną wcześniej prędkością \(c/10\), składającego się jedynie z 28 żywych komórek.)
Oprócz tego, że Grę w życie z całą pewnością można zaliczyć do matematyki rekreacyjnej, wiążą się z nią też całkiem poważne rozważania matematyczne. Sam Conway udowodnił na przykład, że w Życiu można skonstruować tzw. uniwersalną maszynę Turinga, czyli ,,komputer” dysponujący ,,pamięcią” i mogący wykonać dowolny ,,program”. Skonstruowano też w Życiu ,,komputer” symulujący… Grę w życie.
Niezależnie od badań powodowanych po prostu ciekawością, wielbiciele Życia mają też swoiste poczucie humoru. W Życiu skonstruowano np. zegar cyfrowy; w internecie można też znaleźć programy pozwalające przetworzyć dowolny obraz na podobną do niego martwą naturę. W 2014 roku grupa entuzjastów (wydaje się, że słowo ,,szaleńców” nie byłoby tu nie na miejscu) zaprojektowała w Życiu model ,,prawdziwego” komputera, na którym zaimplementowano wersję gry w Tetris. (Podobnie jak w prawdziwej inżynierii, rozpoczęli oni od wytworzenia ,,przewodów” i ,,bramek logicznych”; stąd już niedaleko do pamięci i procesora.) Praca nad tym zajęła grupie półtora roku, a układ ma rozmiary rzędu około trzech na dziesięć milionów ,,kratek”. (Zaprogramowanie symulatora tak dużych układów, działającego z przyzwoitą prędkością, jest poważnym wyzwaniem algorytmicznym. Nawet początkujący programista z łatwością napisze program symulujący Życie na małej planszy. Napisanie programu, który działa z taką ilością danych, wymaga biegłej znajomości bardzo pomysłowych technik programowania i algorytmiki.)
Gra w życie to jedno z tych miejsc, gdzie nawet amator, który nie poświęcił wielu lat na studiowanie matematyki, może zobaczyć jej piękno, a nawet odkryć coś nowego — a&ngsp;przynajmniej zobaczyć, że zajmowanie się matematyką może dostarczyć sporej satysfakcji.
Artykuł został przygotowany przy wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.