Ruch swobodny
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
Tak brzmi oryginalne sformułowanie zasady (nazywanej dziś I zasadą dynamiki Newtona) mówiącej, że cząstka swobodna (taka, na którą nie działa żadna siła) spoczywa lub porusza się ruchem jednostajnym wzdłuż linii prostej. Nie można prościej? Można, jeśli wprowadzi się pojęcie czasoprzestrzeni. Wtedy wystarczy powiedzieć, że trajektorią cząstki swobodnej jest prosta.
Wydaje się, że I zasada dynamiki wynika z prostej obserwacji, a sformułowana jest w języku oczywistych pojęć takich jak linia prosta, spoczynek, ruch jednostajny czy swoboda. Kto jednak interesuje się matematyką wie, jakie ukryte bogactwo potrafi tkwić w pozornie prostych pojęciach.
Rozważmy cząstkę poruszającą się w świecie dwuwymiarowym (na płaszczyźnie), np. krążek sunący po lodowisku.
Rys. 1
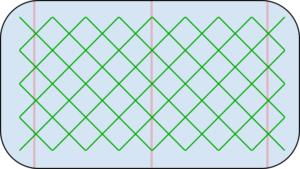
Żeby precyzyjnie opisać położenie krążka tworzymy mapę lodowiska nanosząc na nie siatkę „południków” i „równoleżników”.
Rys. 2
Z pomocą takiej siatki każdy punkt lodowiska zyskuje swój „adres” w postaci dwóch liczb \(x^{(1)}\) i \(x^{(2)}\) (1 i 2 to wskaźniki numerujące współrzędne, a nie potęgi!). Trajektorię krążka możemy teraz rozumieć jako odwzorowanie przyporządkowujące każdej chwili czasu \(t\) parę współrzędnych
\(t\mapsto (x^{(1)},x^{(2)}).\)
Dygresja o pochodnych: Niech \(t\) będzie dowolną (nie przesadzajmy z tą dowolnością – fizycy zajmują się głównie „porządnymi” funkcjami) funkcją czasu. Zdefiniujmy następująco
\(\Delta f(t,\Delta t)\equiv f(t+\Delta t)-f(t)\)
przyrost funkcji (zależny od czasu \(t\) i od przyrostu czasu \(\Delta t\)). Analiza matematyczna uczy nas, że (choć nie jest to wcale oczywiste) dla dostatecznie małego \(\Delta t\) przyrost funkcji jest proporcjonalny do przyrostu czasu \(\Delta f\sim\Delta t\). Współczynnik proporcjonalności (który może zależeć od \(t\) , ale nie od \(\Delta t\)) oznaczamy \(\dot{f}\) i nazywamy pochodną funkcji po czasie. Dalej, traktując tak obliczoną wielkość jako funkcję czasu \(\dot{f}(t)\) możemy wyznaczyć jej pochodną (pochodną pochodnej), którą oznaczymy \(\ddot{f}\). Dla dalszej lektury wystarczą Ci Czytelniku, pochodne kilku funkcji (\(a,b,\omega\) – to stałe)
| \(f\) | \(\dot{f}\) | \(\ddot{f}\) |
|---|---|---|
| \(at+b\) | \(a\) | \(0\) |
| \(\sin(\omega t)\) | \(\omega\cos(\omega t)\) | \(-\omega^2 \sin(\omega t)\) |
| \(\cos(\omega t)\) | \(-\omega\sin(\omega t)\) | \(-\omega^2 \cos(\omega t)\) |
Traktując współrzędne jako funkcje czasu \(x^{(1)}(t)\) i \(x^{(2)}(t)\) możemy obliczać ich pochodne i korzystając z tego narzędzia sformułować I zasadę dynamiki w postaci dwóch równań
\[\ddot{x}^{(j)}=0,\quad (j=1,2),\quad \textrm{ (rów. 1) }\]
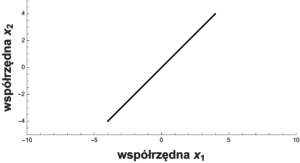
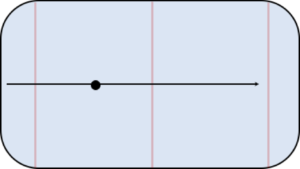
które powinna spełnić trajektoria cząstki swobodnej. Trajektoria na diagramie tworzy linię prostą, tak jak linię prostą tworzy rzeczywisty ruch krążka na lodzie. Krążek traktujemy jak cząstkę swobodną.
Rys. 3
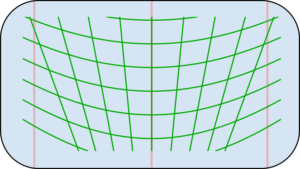
Widać, że prostej w świecie realnym (fizyka) odpowiada prosta w abstrakcyjnym modelu (matematyka). Taka zgodność często prowadzi nas w kierunku utożsamienia przestrzeni realnej z przestrzeniami abstrakcyjnymi. Czy jednak nie jest ona w jakiejś mierze kwestią przypadku? Zastosujmy inną siatkę „południków” i równoleżników”. Wynikające z takiej siatki współrzędne oznaczamy \(y^{(j)}\), \((j=1,2).\)
Rys. 4
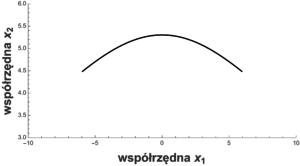
Trajektoria krążka \(t\mapsto (y^{(1)},y^{(2)})\) narysowana w przestrzeni (abstrakcyjnej) nowych współrzędnych
Rys. 5
\[\ddot{y}^{(j)}+\Gamma_{mn}^{j}\dot{y}^{(m)}\dot{y}^{(n)}=0, \quad (j, m, n = 1, 2) \quad \textrm{ (rów. 2) }\]
\[\ddot{y}^{(j)}+\Gamma_{1,1}^{j}\dot{y}^{(1)}\dot{y}^{(1)} + \Gamma_{1,2}^{j}\dot{y}^{(1)}\dot{y}^{(2)} + \Gamma_{2,1}^{j}\dot{y}^{(2)}\dot{y}^{(1)}+\Gamma_{2,2}^{j}\dot{y}^{(2)}\dot{y}^{(2)}\quad (j=1,2)\]
Ruch pod wpływem grawitacji
\[x^{(1)}=\cos(\omega t), \quad x^{(2)} = \sin(\omega t), \quad\textrm{ (rów. 3) }\]
Rys. 6
Ogólnie, działające siły „spychają” cząstki z linii geodezyjnych w stopniu zależnym od ich masy. Grawitacja jest pod tym względem nietypowa. Trajektoria cząstki poruszającej się pod wpływem grawitacji, podobnie jak trajektoria cząstki swobodnej nie zależy od jej masy. To uderzające podobieństwo ruchu swobodnego i ruchu pod wpływem grawitacji sugeruje, żeby wykluczyć grawitacje z katalogu „zwykłych” sił. Jak zatem opisać jej wpływ na ruch ciał? Jeśli grawitacja traci status siły, to ruch pod jej wpływem powinniśmy uznać za swobodny. Zatem cząstka poruszająca się pod wpływem grawitacji powinna także poruszać się po linii geodezyjnej.
Zadanie do wykonania: Sprawdź, Czytelniku, czy trajektoria dana równaniem 3 spełnia równania 1.
Porażka? Jeszcze nie. Ze współrzędnymi kartezjańskimi \(x^{(j)}\) związaliśmy zerowe współczynniki krzywizny \(\Gamma_{mn}^{j}=0\), jednak dotyczyło to przypadku z zerową grawitacją. Może źródło grawitacji „generuje” niezerowe współczynniki krzywizny tak, że kołowa orbita staje się geodezyjną. Niestety, nie istnieją współczynniki krzywizny takie, żeby trajektoria dana równaniem 3 spełniała równanie 2.
Czasoprzestrzeń
\[x^{(0)}=t, \quad x^{(1)}=\cos(\omega t), \quad x^{(2)}=\sin(\omega t), \quad\textrm{ (rów. 4) } \]
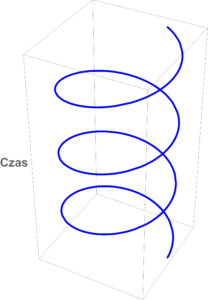
Zadanie do wykonania: Czy helisa może być linią geodezyjną?
Podpowiedź: Wyzeruj wszystkie współczynniki krzywizny poza dwoma. Niech \(\Gamma_{0,0}^{j}=0\) dla \(j=1,2\) będą równe odpowiednim składowym natężenia pola grawitacyjnego \(\vec{{}g}\)
\(\Gamma_{00}^{j}=-g^{(j)}\quad (j=1,2).\) (rów.5)
Wektor natężenia pola grawitacyjnego \(\vec{{}g}\) to nic innego jak przyspieszenie cząstki swobodnej, umieszczonej w polu grawitacyjnym (przy powierzchni Ziemi wartość \(g\) wynosi \(9,81\ m/s^2\)). Dla punktów na orbicie o jednostkowym promieniu mamy \(g^{(j)}=- \omega^2 x^{(j)}\) (dwójka przy omedze to tym razem kwadrat, a nie wskaźnik!). Wykorzystaj, drogi Czytelniku fakt, że \(\dot{x}^{(0)}=1.\)
To, że helisa może być uznana za geodezyjną nie jest przypadkiem. W ogólnym przypadku ruchu w trójwymiarowej przestrzeni czasoprzestrzenną trajektorią cząstki swobodnej poruszającej się w polu grawitacyjnym zgodnie z fizyką newtonowską jest geodezyjna, o ile przyjmiemy, że \(\Gamma_{00}^{j}=-g^{(j)}\quad (j=1,2,3)\) , a pozostałe współczynniki krzywizny się zerują.
Ten fakt umożliwia mówienie o newtonowskiej grawitacji w całkowicie nowym języku. Trajektorią cząstki swobodnej w czasoprzestrzeni jest geodezyjna, która w zerowym polu grawitacyjnym (\(\Gamma_{mn}^{j}=0\)) przyjmuje kształt prostej (w odpowiednich współrzędnych). Włączenie pola grawitacyjnego powoduje (wyrażając się w tradycyjnym języku) zepchnięcie cząstki z geodezyjnej. W nowym języku po włączeniu grawitacji cząstka nadal porusza się po geodezyjnej, która jednak przybiera inny kształt (np. helisy), na skutek zakrzywienia współrzędnych (\(\Gamma_{00}^{j}\neq 0\)).
Zakrzywienie współrzędnych czy zakrzywienie czasoprzestrzeni
Pozostaje do rozstrzygnięcia, czy grawitacja zakrzywia czasoprzestrzeń, czy tylko współrzędne. Rysunek 4 przekonuje, że rozróżnienie to jest istotne. Przecież wprowadzenie krzywoliniowych współrzędnych nie zakrzywiło powierzchni lodowiska. Płaską będzie ta przestrzeń, która dopuszcza istnienie współrzędnych kartezjańskich \(\Gamma_{mn}^j=0\), niezależnie od tego jakimi współrzędnymi aktualnie się posługujemy. Musimy więc odpowiedzieć na (niełatwe) pytanie, czy można dobrać w czasoprzestrzeni z grawitacją (\(g^{(j)}\neq 0\)) współrzędne, dla których \(\Gamma_{mn}^j=0\). Niech to pytanie, będzie dla Ciebie Czytelniku zachętą do studiowania geometrii różniczkowej. Nauczysz się wtedy definiować obiekty (tensory), które pozwolą Ci odpowiadać na takie pytania bez konieczności sprawdzania wszystkich możliwych współrzędnych. Jednym z takich obiektów jest tensor Ricciego \(R\). Dla newtonowskiej czasoprzestrzeni z niezerową grawitacją \(\Gamma_{00}^j=-g^{(j)}\neq 0\) jedna ze składowych tensora Ricciego (pozostałe zerują się) związana jest z rozkładem masy (\(\rho\) to masa przypadająca na jednostkę objętości, \(G\) to stała grawitacji)
\[R_{00}=8 \pi G \rho.\quad\textrm{ (rów. 6) }\]
Warunkiem koniecznym (choć niewystarczającym) płaskości czasoprzestrzeni jest zerowanie się wszystkich składowych tensora Ricciego. Wniosek wypływający z równania 6 jest taki: grawitacja zakrzywia czasoprzestrzeń, a rozkład masy decyduje o jej geometrii.
Natomiast I zasadę dynamiki można uogólnić następująco: cząstki swobodne (w zerowym bądź niezerowym polu grawitacyjnym) poruszają się po liniach geodezyjnych czasoprzestrzeni.
Zdziwienie
Pozostaje wyrazić zdziwienie, że opis grawitacji w języku zakrzywienia czasoprzestrzeni nie został zaproponowany znacznie wcześniej – w ramach fizyki newtonowskiej, np. przez Laplace’a lub Riemanna, ale musiał czekać na Einsteina. Niezbędny formalizm matematyczny był przecież dostępny. Jednak dopiero potrzeba zrozumienia grawitacji w ramach relatywistycznie niezmienniczej teorii Einsteina stworzyła wystarczająco silną motywację do zmiany sposobu myślenia o grawitacji.
Artykuł został przygotowany przy wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.