Niniejszym wpisem inicjujemy serię animacji i interaktywnych modułów, które ilustrują ciekawe twierdzenia, obiekty i problemy matematyczne.

W tym odcinku prezentujemy zdumiewające twierdzenie dotyczące zwyczajnego trójkąta na płaszczyźnie i należące do klasycznej geometrii płaszczyzny, lecz udowodnione dopiero w 1899 roku przez brytyjskiego matematyka Franka Morleya.

Twierdzenie (Frank Morley, 1899):

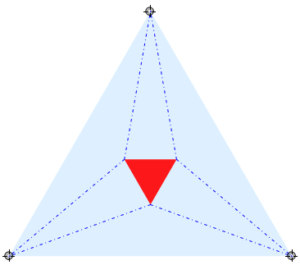
Niech dany będzie trójkąt dowolny $\Delta ABC$ na płaszczyźnie. Prowadzimy z kątów $\sphericalangle A$, $\sphericalangle B$, $\sphericalangle C$ po dwie półproste. Pary półprostych wyznaczają trójpodział każdego z kątów. Półproste z dwóch sąsiadujących kątów przecinają się w punkcie. Trójkąt utworzony z trzech punktów przecięcia jest zawsze równoboczny.

Dowód tego twierdzenia można wykonać na wiele różnych interesujących sposobów. Poniżej przedstawiamy moduł, który obrazuje możliwe ustawienia trójkąta względem ustalonego trójkąta. Poruszając szarymi celownikami można uzyskać dowolny układ trzech punktów i przekonać się, że zawsze uzyskany trójkąt będzie równoboczny.