Okrąg dziewięciu punktów

W 1822 roku Karl Wilhelm Feuerbach zauważył, że sześć charakterystycznych punktów trójkąta – środki boków oraz spodki wysokości – leżą na wspólnym okręgu. Krótko po Feuerbachu, matematyk Orly Terquem niezależnie udowodnił istnienie okręgu i jako pierwszy zwrócił uwagę, że leżą na nim również środki odcinków łączących wierzchołki z ortocentrum.

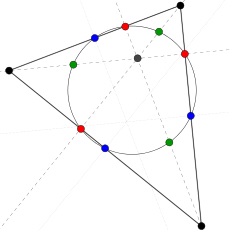
Okrąg dziewięciu punktów znany także jako okrąg Feuerbacha lub okrąg Eulera, jest to okrąg, który przechodzi przez dziewięć charakterystycznych punktów dowolnego trójkąta. Punktami tymi są:

• środki boków (zaznaczone na niebiesko)
• spodki trzech wysokości (zaznaczone na czerwono)
• punkty dzielące na połowy trzy odcinki, które łączą wierzchołki tego trójkąta z jego ortocentrum (zaznaczone na zielono)

Zainteresowanych dowodem okręgu dziewięciu punktów odsyłam do książki „Wykłady z geometrii” autorstwa Ewy Marchow.

Twierdzenie Feuerbacha

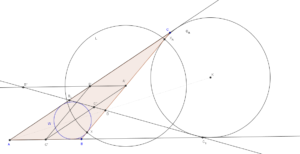
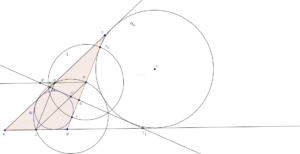
W dowolnym trójkącie okrąg dziewięciu punktów jest styczny wewnętrznie do okręgu wpisanego i zewnętrznie do trzech okręgów dopisanych. Punkt styczności okręgu wpisanego i okręgu dziewięciu punktów nazywa się często punktem Feuerbacha.

Wizualizacja twierdzenia

Przesuwając w dowolne miejsca wierzchołki trójkąta można zauważyć, że okrąg dziewięciu punktów (zaznaczony kolorem czarnym) zawsze jest styczny do okręgu wpisanego (kolor czerwony) jak i okręgów dopisanych do trójkąta (kolor niebieski).
Na wizualizacji zaznaczone są także punkty charakterystyczne okręgu dziewięciu punktów, ich kolory odpowiadają kolorom użytym w definicji.

Definicja (okręgu dopisanego)

Okrąg dopisany do trójkąta – okrąg styczny do jednego z boków trójkąta oraz przedłużeń dwóch pozostałych boków. Jego środek znajduje się w punkcie przecięcia dwusiecznych odpowiednich kątów zewnętrznych. Okrąg ten ma dokładnie jeden punkt wspólny z trójkątem.

Oznaczenia użyte w dowodzie:
$[A,B]$ – odcinek o końcach $A$ i$ B$
$(AB)$ – prosta przechodząca przez punkty A i B
${\iota}_L(A)$ – inwersja punktu A względem okręgu L

Dowód twierdzenie Feuerbacha (1)

Zakładamy, że $b=|AC|>|AB|=c$, $X$ i $X_A$ są punktami styczności boku $[B,C]$ z okręgami $W$ i $O_A$ odpowiednio, $L$ jest okręgiem o środku w punkcie $A’$ i promieniu $[A’,X]$. Zauważmy, że $|A’X|=|A’X_A|$, gdyż $|BX|=|CX_A|=p-b$ (gdzie p jest połową obwodu trójkąta). Zatem promień okręgu $L$ jest równy $$r_L=\frac{b-c}{2}$$ Okrąg $L$ jest prostopadły do $W$, gdyż styczna do $W$ przechodzi przez środek $L$. Podobnie $L$ jest prostopadły do $O_A$. Zatem inwersja względem okręgu $L$ przekształca $W$ na $W$ a $O_A$ na $O_A$.

$D$ niech oznacza punkt przecięcia boku $[B,C]$ z dwusieczną $\sphericalangle(BAC)$. Druga wspólna styczna obu okręgów przechodząca przez $D$ przecina boki $[A,C]$ i $[A,B]$ w punktach $B_1$ i $C_1$ odpowiednio.

$\Delta (A,B,C)$ przystaje do trójkąta $\Delta(A,B_1,C_1)$, gdyż jeden z nich jest obrazem drugiego w symetrii względem prostej $(AD)$. Ponadto, ponieważ

$|BD|+|CD|=a$ oraz $\dfrac{|BD|}{c}=\dfrac{|CD|}{b}$

Wówczas

$|BD|=\dfrac{ac}{b+c}$ i $|CD|=\dfrac{ab}{b+c}$.

Oznaczmy przez $B”$ punkt przecięcia prostej $(A’B’)$ z prostą $(B_1 C_1)$ oraz przez $C”$ punkt przecięcia prostej $(A’C’)$ z prostą $(B_1C_1)$. Trójkąty $\Delta (A,B_1,C_1)$ i $\Delta(A’,C”,B”)$ są podobne, gdyż oba są podobne do $\Delta(C’,C”,C_1)$, zatem trójkąt $\Delta(A’,C”,B”)$ jest podobny do trójkąta $\Delta(A,B,C)$.

Stąd
$$\frac{|A’B”|}{|A’C”|}=\frac{|AC|}{|AB|}=\frac{b}{c}$$

Jednocześnie trójkąt $\Delta(A’,D,C”)$ jest podobny do trójkąta $ \Delta(C,D,B_1)$, gdyż $(AC)||(A’C”)$, zatem

$$\frac{|A’D|}{|CD|}=\frac{|A’C”|}{|B_1C|}$$

Mamy więc
$$|A’C”|=\dfrac{(\dfrac{a}{2}-\dfrac{ac}{b+c})(b-c)(b+c)}{ab}=\dfrac{(b-c)^2}{2b}$$
Ponieważ
$$\frac{|A’B”|}{|A’C”|}=\frac{|AC|}{|AB|}=\frac{b}{c}$$
więc
$$|A’B”|=\frac{b}{c} \frac{(b-c)^2}{2b}=\frac{(b-c)^2}{2c}$$
Zatem
$$|A’B’||A’B”|=\frac{c}{2} \frac{(b-c)^2}{2c}=\frac{(b-c)^2}{4}=(r_L)^2$$
oraz
$$|A’C’||A’C”|=\frac{b}{2} \frac{(b-c)^2}{2b}= \frac{(b-c)^2}{4}=(r_L)^2$$
a to znaczy, że ${\iota}_L (B’)=B”$ i ${\iota}_L (C’)=C”$. Obrazem prostej $(B”C”)$ w inwersji względem $L$

jest okrąg przechodzący przez $A’$,$B’$ i $C’$, a więc okrąg dziewięciu punktów trójkąta $\Delta(A,B,C)$. Obrazem okręgu $W$ w tej inwersji jest $W$, obrazem okręgu $O_A$ jest $O_A$, zatem zarówno $W$ jak $O_A$ mają po jednym punkcie wspólnym z okręgiem dziewięciu punktów, jako że prosta $(B”C”)$ jest styczna zarówno do $W$ jak do $O_A$.

(1) E. Marchow, Wykłady z geometrii, Poznań 2010.