Ten nieznośny spam
Zastanawiałeś się kiedyś, dlaczego niektóre z Twoich skrzynek pocztowych są codziennie bombardowane reklamami dotyczącymi zapobiegania wypadaniu włosów, podczas gdy inne nie? Albo dlaczego kiedy mówisz do swojej komórki, że szukasz rozkładu pociągów z Poznania do Szamotuł, to Twoja wypowiedź zamienia się na zapytanie w wyszukiwarce internetowej dokładnie związane z Twoim problemem?
Jeżeli widzisz teraz kilka milionów osób, które siedzą po drugiej stronie naszego globu i codziennie czytają i filtrują Twoją przychodzącą pocztę, to muszę Cię pocieszyć, że nikt tego całego spamu, jaki powstaje w internecie na szczęście nie musi czytać. Nikt też nie musi czekać po drugiej stronie słuchawki $24$ godziny na dobę w nadziei, że zadasz pytania związane tylko z rozkładem kolejowym w Polsce.
Dlaczego? Ponieważ możemy wykorzystać do takich prac pewien wynalazek, który nigdy się nie nudzi, nie męczy i co więcej — zaczyna mylić się rzadziej niż ludzie. Myślę tutaj oczywiście o komputerze, komórce, tablecie czy jakiejkowiek innej maszynie, która może przetwarzać ciąg zer i jedynek. Wystarczy, że zaprojektujemy odpowiedni model i nauczymy naszą maszynę (ang. machine learning), jak powinna ten model wykorzystywać. Brzmi skomplikowanie? Nic bardziej mylnego. Postaram się tutaj opisać w największym skrócie i uproszczeniu, jak taki model możemy zaprojektować i nauczyć go wnioskować jak człowiek.
Zamiast klasyfikować e-maile, spróbujemy stworzyć maszynę, która — widząc zdjęcie — będzie potrafiła poprawnie stwierdzić czy zaobserwowała psa, czy kota.
Trochę nudnej matematycznej terminologii
Według książkowych definicji uczenie maszynowe to konstruowanie algorytmów które uczą się i wnioskują (ang. infer) na podstawie danych (ang. data). Zacznijmy od końca — czym są dane? Można odpowiedzieć na to bardzo trywialnie — to tak naprawdę wszystko co nasza elektroniczna maszyna może przetworzyć. Jak już wspomniałem wcześniej, spróbujemy stworzyć model, który będzie klasyfikować zdjęcia do odpowiedniej grupy. Naszymi danymi będzie zatem zbiór zdjęć, z którego każde będzie zbudowane z $m \times m$ pikseli oraz przypisanej klasy. Możemy to przedstawić w skrócie jako:
$$\mathcal{D} = \{ x_n, c_n\}_{n=1}^N,$$
gdzie $x_n$ to piksele tworzące zdjęcie $n$, $c_n$ to klasa związana ze zdjęciem, np. $\{pies\}$ albo $\{kot\}$, a $N$ to liczba wszystkich zdjęć treningowych, jakie posiadamy.
Przejdźmy do drugiej części naszej definicji — co tak naprawdę nasz model ma wnioskować? Z probabilistycznego punktu widzenia zarejestrowane obrazy są realizacją nieznanego nam zjawiska dla wybranego stanu świata. Wow, zabrzmiało to pompatycznie, ale znaczy to tylko tyle, że nasz model ma przewidzieć, jaką klasę przypisać do zdjęcia, które właśnie zostało mu pokazane, czyli wywnioskować, jaki stan świata został zaobserwowany. Wykorzystamy do tego pewną funkcję, nazwijmy ją $f$, której argumentem może być zbiór pikseli (zdjęcie), natomiast wartością jedna z klas. W matematycznej notacji zapiszemy to jako:
$$f\colon \text{zbiór zdjęć} \rightarrow \{ \text{kot, pies} \}.$$
Sieci neuronowe
Do tej pory nie wspomniałem ani słowem, jak tak naprawdę nasz model ma wyglądać. Gdyby zapytać $100$ profesorów zajmujących się sztuczną inteligencją, jaki model wydaje się być najlepszy dla naszego problemu, usłyszelibyśmy co najmniej $101$ różnych odpowiedzi — i każda z nich na swój sposób byłaby poprawna. Jednakże już od początku rozwoju sztucznej inteligencji naukowcy próbowali opracować model, który w jakiś sposób będzie podobny do naszego mózgu — ideału inteligencji, jaki jest nam znany. Co jest podstawowym budulcem każdego ludzkiego mózgu? Oczywiście neurony, których średnio mamy około $100$ miliardów! Spróbujmy więc zaprojektować model, który będzie przypominać (w dużym uproszczeniu) nasz mózg — poniższy rysunek przedstawia naszą prototypową sieć neuronową:
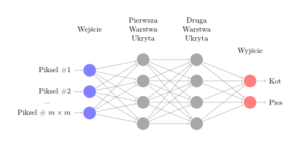
Mamy w niej warstwę wejścia, czyli piksele, które widzimy. Następnie możemy mieć kilka warstw „ukrytych”, które przetwarzają piksele w taki sposób by na ostatniej warstwie, wyjścia, wydać poprawny werdykt w sprawie klasy, do której zdjęcie należy. Choć komputery cały czas przyspieszają1, $100$ miliardów to ciągle trochę za dużo jak na dzisiejsze możliwości i obecnie największe modele posiadają tylko $50000$ „neuronów”.
Mamy zatem w końcu namacalną formę naszej funkcji $f$. Zapewne teraz zastanawiasz się, co znaczy to magiczne słowo przetwarzają, którego użyłem, by opisać linie łączące neurony z różnych warstw. Są to parametry naszej funkcji (zwane często wagami, ang. weights), które oznaczymy przez $w$. Naszym zadaniem będzie „nauczyć” je, że odpowiednie ułożenie pikseli (dla nich to po prostu ciąg cyfr) może oznaczać ogon psa, a nie kota.2
Ponieważ to, jaką klasę nasza funkcja będzie zwracać, zależy w zupełności od naszych wag, będziemy to przedstawiać przez zapis $f(x; W)$, gdzie $W$ oznacza zbiór wszystkich wag naszej sieci.
Uczymy się
Mamy już nasz model, czas nauczyć go czegoś pożytecznego. Dla danego zdjęcia nasz model powinien zwracać dwuwymiarowy wektor, który będzie składać się z zera i jedynki. Miejsce jedynki w wektorze będzie informować o tym, do jakiej klasy dane zdjęcie zostało zaklasyfikowane w oparciu o nasz model. Zdefiniujmy teraz przykładową3 funkcję straty (ang. loss function), która będzie zliczać, ile razy się pomyliliśmy, po pokazaniu maszynie wszystkich zdjęć treningowych jakie posiadamy:
$$L(W) = \sum_{x_n \in \mathcal{D}} (f(x_n; W) – c_n)^2$$
Jeżeli dla danego zdjęcia $x_n$, które przedstawia kota, nasz model zwróci wektor odpowiadający przyporządkowaniu do klasy pies, to nasza strata się powiększy.
Mamy już wszystkie elementy potrzebne do uczenia naszego prototypowego modelu. Powstaje teraz pytanie w jaki sposób trenować nasze wagi $W$, by przybrały odpowiednie wartości, które w ostatecznym rachunku sprawią, że kiedy przetworzymy zdjęcie kota, algorytm wyrzuci jedynkę na odpowiednim miejscu, czyli przypisze zdjęcie do odpowiedniej klasy.
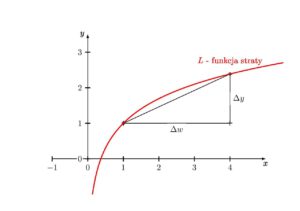
Modele służące do klasyfikacji i opisu obrazów lub rozpoznania mowy mogą mieć $100$ milionów wag. Nawet gdyby były istniało rozwiązanie jawne zależności pomiędzy nimi (choć nie istnieje), poszukiwanie tego rozwiązania zajęłoby lata. Istnieje rozwiązanie trochę prostsze — załóżmy, że losowo wybraliśmy wagi startowe $W$. Zauważmy, że pochodna funkcji $L$ względem danej wagi $w$, $\frac{\partial L}{\partial w}$, informuje nas, jak nasza strata wzrośnie względem przyrostu wartości naszego parametru — spójrz na poniższy rysunek.
Jeżeli zatem przyrost jest duży, to znaczy, że warto trochę zwiększyć wartość naszego parametru co doprowadzi do zwiększenia straty. Ale, ale — przecież naszym zadaniem jest minimalizowanie straty! Nic prostszego, weźmy wartość pochodnej z przeciwnym znakiem. W przypadku funkcji, która ma wiele zmiennych (w naszym przypadku bardzo wiele zmiennych), uogólnienie pochodnej przybiera postać gradientu:
$$\nabla L = \left[ \frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, …, \frac{\partial L}{\partial w_{99~ 999~ 999}} , \frac{\partial L}{\partial w_{100~000~000} }\right].$$
Nasze uczenie bedzie zatem polegało na sekwencyjnym aktualizowaniu wag:
$$ W’ = W – \eta\nabla L,$$
gdzie $\eta$ wyznacza prędkość z jaką chcemy nasz model uczyć (ang. learning rate). Jest tylko jeden mały problem z taką aproksymacją, o której rzadko który praktyk wspomina — uczenie tak dużych struktur trwa często ponad jeden tydzień. Jeżeli zatem gdzieś popełniliście mały błąd w kodzie i teraz go naprawiacie, upewnienie się, że wszystko znowu działa jak należy, jest „lekko” czasochłonne.
To dopiero początek
Jeżeli wydaje Ci się, że ta tematyka jest interesująca i chciałbyś spróbować swoich sił, to nie możesz wymarzyć sobie do tego lepszego momentu. Wszystkie metody, które obecnie są wykorzystywane przez największych gigantów jak Google, Facebook czy Microsoft powstały najpóźniej kilka lat temu. Prawdziwe możliwości przed sztuczną inteligencją dopiero się otwierają i masz wielką szansę brać w tym udział! Ten artykuł to oczywiście tylko małe wprowadzanie i sieć jest pełna świetnych kursów i materiałów, które są dostępne całkowicie za darmo — gorąco zachęcam do ich wykorzystywania.
Ten artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną z Fundacji mBanku na realizację projektu „Potęga matematyki”.