Uczniowie pewnego liceum otrzymali do rozwiązania w domu następujące zadanie:

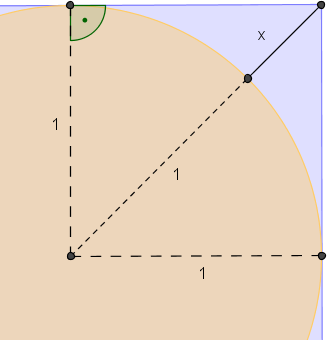
Na kole o promieniu jednostkowym opisano kwadrat. W jakiej odległości od wierzchołka kwadratu znajduje się najbliższy wierzchołkowi punkt koła? Przyjmij, że \(\sqrt{2} \approx 1,41.\)

Większości uczniów zadanie wydawało się proste, wyjątkowo proste. Niektórzy, pewni siebie, szybko zamknęli zeszyty tego wieczoru. Inni jednak zaczęli podejrzewać (i słusznie), że nauczyciel, proponując takie zadanie, miał jakiś ukryty cel.

Następnego dnia w czasie prezentacji rozwiązań zadań, na tablicy pojawiły się trzy sposoby rozwiązania zadania. Co jednak ciekawsze — przybliżenia długości poszukiwanego odcinka zostały przez autorów zapisane różnie: \(0{,}41\) oraz \(0{,}414\). Zosia, autorka ostatniej propozycji rozwiązania, upierała się, że w uzyskanym przez nią przybliżeniu wszystkie cyfry są znaczące (pewne). Czy miała rację?

Rozwiązanie Wojtka zawierało następujące równanie (patrz poniższy rysunek):
\[
x + 1 = \sqrt{2},
\]
skąd
\[
x = \sqrt{2} -1 \approx 0{,}41.
\]
Taki sposób rozwiązania (i odpowiedź) dominował w klasie.

Andrzej, przekorny z natury, postanowił problem opisać równaniem kwadratowym:
\[
(x + 1)^2 = 1^2 + 1^2,
\]
które przekształcił do postaci:
\[
x^2 + 2x – 1 = 0
\]
i rozwiązał, korzystając ze wzorów na pierwiastki trójmianu kwadratowego. Jedno z rozwiązań było liczbą dodatnią, więc uczeń zakończył swą prezentację, pisząc na tablicy:
\[
x = \sqrt{2} -1 \approx 0{,}41.
\]

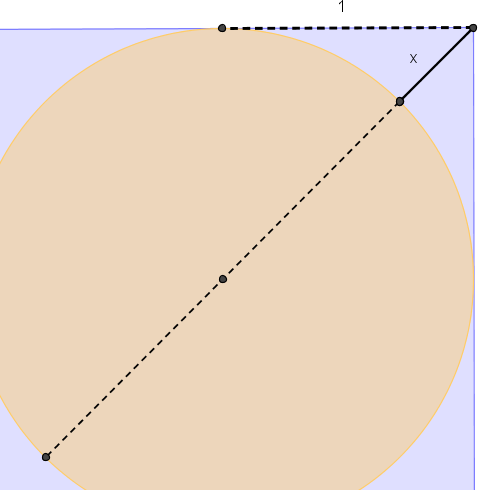
Na końcu swoje rozwiązanie zapisała Zosia. Koledzy i koleżanki spodziewali się, że ta dziewczyna, uczestniczka konkursów matematycznych, może ich czymś zaskoczyć. I tym razem Zosia nie rozczarowała. Zastosowała bowiem… twierdzenie o siecznych i otrzymała równanie (patrz poniższy rysunek):
\[
x (\sqrt{2} +1) = 1 \cdot 1,
\]
a stąd
\[
x = \frac{1}{\sqrt{2} +1} \approx 0{,}414.
\]

Dziewczyna przekonywała, że skoro przybliżenie
\[
\sqrt{2} \approx 1{,}41
\]
zawiera trzy pewne cyfry (tj. \(1\) nie powstało przez zaokrąglenie w górę), to w konsekwencji pewne są też trzy cyfry ilorazu
\[
\frac{1}{2,41} \approx 0{,}414.
\]
Na poparcie swej tezy zapisała na tablicy i objaśniła oszacowanie:
\[
0{,}414 < \frac{1}{2,415} < 0{,}415. \] Po prezentacjach rozwiązań w klasie wywiązała się dyskusja. Dyskusja była pouczająca, więc nauczyciel przez dłuższy czas jej nie przerywał. Zosia jeszcze dwukrotnie musiała objaśniać istotne znaczenie swoich rozważań. Przekonywała, że np. w przypadku koła o promieniu 100 m jej przybliżenie pozwoliłoby podać poszukiwaną odległość z dokładnością do 10 cm, co w praktyce obliczeń technicznych może być istotne. Większość wątpiących w końcu przyznała rację Zosi. Inni pozostali nieprzekonani. Nie mając argumentów, ograniczali się to stwierdzeń w rodzaju ,,inżynierowie w obliczeniach i tak posługują się bardziej dokładnymi przybliżeniami liczby \(\sqrt{2}\), więc nasza dyskusja jest bezcelowa''. W końcu głos zabrał nauczyciel i zwrócił uwagę na to, że choć \[ \sqrt{2} -1 = \frac{1}{\sqrt{2} +1}, \] to w rachunku przybliżonym wyrażenia te wcale nie muszą być równoważne. Wyjaśnił, że częstym powodem źródłem złej dokładności wyniku obliczeń przybliżonych jest odejmowanie, w którym może dojść do znoszenia się składników (ang. cancellation).¹ Nauczyciel podkreślił, że różnica dwóch prawie identycznych liczb może mieć bardzo małą dokładność względną, np. jeśli
\[
x=0{,}1234\pm\frac{1}{2}\cdot{10}^{-4}
\]
oraz
\[
y=0{,}1233\pm\frac{1}{2}\cdot{10}^{-4},
\]
to
\[
x-y = 0{,}0001\pm 0{,}0001
\]
i oszacowanie błędu jest tak samo duże, jak otrzymana suma.

Uczniowie przedstawionej wyżej klasy mieli szczęście, że ich nauczyciel matematyki uczył ich również informatyki. Jedną z kolejnych lekcji tego przedmiotu poświęcił zagadnieniom algorytmów niestabilnych (takim jest tzw. algorytm delty) oraz zadań źle uwarunkowanych numerycznie (takim jest odejmowanie). Przywołał wówczas rozwiązanie Andrzeja, który rozwiązywał równanie kwadratowe
\[
a x^2 + b x + c = 0
\]
stosując znany wszystkim uczniom szkół średnich wzory:
\[
x_1=\frac{-b-\sqrt{\Delta}}{2a}
\]
i
\[
x_2=\frac{-b+\sqrt{\Delta}}{2a},
\]
gdzie
\[
\Delta = b^2 – 4 a c.
\]

Na lekcji informatyki uczniowie mieli okazję się przekonać, że istnieją równoważne wzory, które można by zastosować w niebezpieczeństwie znoszenia się składników, tj. gdy
\[
\lvert 4ac \rvert < b^2.
\]
Mają one odpowiednio postać:
\[
x_1=\frac{2c}{-b+\sqrt{\Delta}}
\]
i
\[
x_2=\frac{2c}{-b+\sqrt{\Delta}}.
\]

Oddzielenie informatyki od matematyki w dużym stopniu zubaża obie te dziedziny. Autor artykułu ma nadzieję, że być może młody Czytelnik zainteresowany matematyką, po lekturze tego artykułu, wybierze w szkole również zajęcia z informatyki rozszerzonej.¹

Zadania dodatkowe

1. Wykaż, że przybliżenie że\(\sqrt{2} \approx 1,41\) jest obarczone błędem (względnym) mniejszym niż \(0{,}3\%\).
2. Wykaż, że odpowiedź \(0{,}41\), uzyskana przez większość uczniów, była obarczona błędem przekraczającym \(1\%\).
3. Uzasadnij poprawność wzorów, o których jest mowa w przedostatnim akapicie.

Przypisy

1. Wybrane algorytmy numeryczne, np. przybliżonego rozwiązywania równań, jak i podstawy arytmetyki komputerowej oraz zagadnienie algorytmów niestabilnych należą do kanonu tematów poruszanych na takich zajęciach.

Autor jest nauczycielem matematyki w V Liceum Ogólnokształcącym w Poznaniu.

Artykuł został nagrodzony w konkursie na artykuł popularnonaukowy przeprowadzony przez Poznańską Fundację Matematyczną dzięki wsparciu pozyskanemu od Miasta Poznań na realizację projektu ,,Potęga matematyki''.