Pierwiastek kwadratowy $\sqrt{2}$ z liczby $2$ to liczba rzeczywista $x > 0$ taka, że $x^2 = 2$. Zobaczymy, że taka liczba $x$ jest niewymierna, tj. dla żadnych liczb całkowitych $a, b > 0$ nie zachodzi równość $x = a/b$.

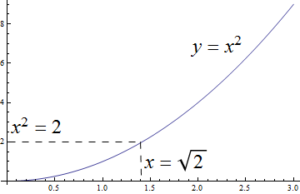
Twierdzenie Dla żadnych dwóch liczb naturalnych $b, c > 0$ nie zachodzi równość $c^2 = 2 b^2$.

Dowód. Przypuśćmy, że istnieją dwie liczby naturalne $b,c>0$ takie, że $c^2=2b^2$. Niech $c_0 = c$ oraz $b_0 = b$. Zatem $c_0^2 = 2 b_0^2$ na mocy naszego przypuszczenia.

Teraz załóżmy, że dla pewnej liczby naturalnej $n \geq 0$ dane są dwie liczby naturalne $c_n$ oraz $b_n$ takie, że $c_n^2 = 2 b_n^2$. Ta równość oznacza, że $c_n^2$ jest liczbą parzystą, a stąd $c_n$ jest liczbą parzystą, tj. $c_n = 2 c_{n+1}$ dla pewnej liczby naturalnej $c_{n+1} > 0$. Tak więc

$$4 c_{n+1}^2 = c_n^2 = 2 b_n^2$$

czyli $2 c_{n+1}^2 = b_n^2$. Zatem $b_n^2$ jest liczbą parzystą, a więc $b_n$ jest liczbą parzystą, tj. $b_n = 2 b_{n+1}$ dla pewnej liczby naturalnej $b_{n+1} > 0$. Korzystając z otrzymanych już wzorów dostajemy

$$2 c_{n+1}^2 = b_n^2 = 4 b_{n+1}^2$$
czyli $c_{n+1}^2 = 2 b_{n+1}^2$. To prowadzi do istnienia dwóch nieskończonych ciągów liczb naturalnych malejących

$$c_0 > c_1 > c_2 > \cdots > 0, \quad b_0 > b_1 > b_2 > \cdots > 0.$$
Istnienie nawet jednego takiego ciągu nie jest możliwe, a zatem nie istnieją liczby naturalne $b, c > 0$ takie, że $c^2=2b^2$, co kończy dowód twierdzenia.

Wniosek. Pierwiastek $\sqrt{2}$ jest liczbą niewymierną, tj. dla żadnych liczb naturalnych $a, b > 0$ nie zachodzi równość $\sqrt{2} = a/b$.

Dowód. Gdyby zachodziła równość $\sqrt{2} = a/b$ dla pewnych liczb naturalnych $a, b > 0$, to zachodziła by też równość $2 = a^2/b^2$, tj. $a^2 = 2 b^2$, co jest niemożliwe na mocy twierdzenia. To kończy dowód wniosku.

Pierwiastek $n$-tego stopnia z liczby pierwszej $p$

Przez liczbę pierwszą $p$ rozumiemy taką liczbę naturalną większą od $1$, która dzieli się tylko przez $1$ oraz $p$.

Twierdzenie. Niech $p$ będzie liczbą pierwszą. Dla żadnej liczby naturalnej $n > 1$ nie istnieją takie liczby naturalne $x$ oraz $y$ różne od $0$, że $x^n = p y^n$.

Dowód. Przypuśćmy, że dla pewnej liczby naturalnej $n > 1$ istnieją takie liczby naturalne $x$ oraz $y$ różne od zera, że $x^n = p y^n$. Niech $a$ oraz $b$ będą największymi liczbami naturalnymi takimi, że $p^a$ oraz $p^b$ dzielą $x$ oraz $y$, odpowiednio.

Wówczas $an$ oraz $bn$ są największymi liczbami naturalnymi takimi, że $p^{an}$ oraz $p^{bn}$ dzielą $x^n$ oraz $y^n$, odpowiednio. Z równości $x^n = p y^n$ wynika, że

$$p^{an} = p p^{bn},$$

a stąd $an = bn + 1$, tj. $n(a-b) = 1$. To jednak jest niemożliwe, bo $n > 1$, co kończy dowód twierdzenia.

Wniosek. Dla każdej liczby naturalnej $n > 1$ pierwiastek $n$-tego stopnia z liczby pierwszej $p$ jest liczbą niewymierną.

Dowód. Gdyby pierwiastek $n$-tego stopnia z liczby pierwszej $p$ był liczbą wymierną, powiedzmy postaci $x/y$ dla pewnych liczby naturalnych $x$ oraz $y$ różnych od $0$, to $(x/y)^n = p$, tj. $x^n = p y^n$, co przeczy twierdzeniu i tym samym kończy dowód wniosku.