Wyobraźmy sobie, że stajemy przed zadaniem obliczenia pola powierzchni pod wykresem pewnej funkcji, na zadanym przedziale $[t_1, t_2]$. Komputery, z racji swojej oszałamiającej wręcz (w porównaniu z mózgiem człowieka) zdolności do szybkiego wykonywania obliczeń, nadają się do tego zadania idealnie. Jako że dana funkcja może być niezwykle skomplikowana, musimy się często jednak zadowolić rozwiązaniami przybliżonymi, o dokładności zależnej od tego, jak wiele czasu możemy poświęcić na oczekiwanie na wynik.
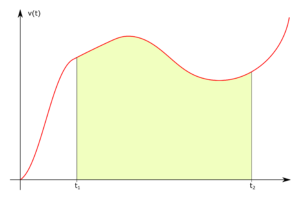
Wydawać by się mogło, że problem obliczania pola powierzchni pod wykresem jest bardzo abstrakcyjny. W praktyce jednak spotyka się go dość często. Przykładowo, jeśli wiemy, jak zmieniała się prędkość obiektu poruszającego się po prostej w czasie (patrz rysunek 1), możemy wyznaczyć drogę, jaką pokonał on w danym przedziale czasu, obliczając wartość pola powierzchni pod odpowiednim fragmentem wykresu.
Rysunek 1. Fragment wykresu funkcji $v(t)$
Jeśli prędkość $v$ jest stała w czasie (a więc gdy mamy do czynienia z~ruchem jednostajnym prostoliniowym), to pole powierzchni pod wykresem na przedziale $[t_1, t_2]$ jest równe $v\cdot(t_2-t_1)$, skąd — jeśli $t_1=0$ — otrzymujemy znany nam wszystkim z lekcji fizyki wzór na drogę: $s=vt$.
Do przybliżania pola powierzchni pod wykresem* w przedziale $[a, b]$ wykorzystuje się procedury numeryczne. Ich idea jest dość intuicyjna: dzielimy zadany przedział na $n$ równych podprzedziałów (oznaczanych $[x_0, x_1], [x_1, x_2],$ $\dots, [x_{n-1}, x_n]$, takich że $x_0 := a$ i $x_n := b$), następnie przybliżamy (w pewien sposób) pole powierzchni pod wykresem w każdym z tych podprzedziałów, by na końcu zsumować otrzymane wyniki.** Dlaczego dzielimy przedział na podprzedziały? Jest to naturalna konsekwencja niemego założenia, że na odpowiednio małym przedziale wykres badanej funkcji da się przybliżyć przy użyciu obiektów, których własności znamy — choćby prostych (wykresów funkcji liniowych) lub parabol (wykresów funkcji kwadratowych).
Metody przybliżania
Pole powierzchni pod wykresem funkcji $f$ na podprzedziale $[x_i, x_{i+1}]$, gdzie $i \in \left\lbrace0, 1, \dots, n-1\right\rbrace$, możemy przybliżyć na niezliczoną liczbę sposobów, spośród których trzy najpopularniejsze to przybliżanie:
- polem prostokąta o szerokości równej $x_{i+1}-x_i = \frac{b-a}{n}$ i wysokości równej wartości funkcji $f$ w środku przedziału (patrz rysunek 2a)
- polem trapezu o długości podstawy równej $x_{i+1}-x_i = \frac{b-a}{n}$ oraz długości lewego boku równej wartości funkcji $f$ w punkcie $x_i$ i długości prawego boku równej wartości funkcji $f$ w punkcie $x_{i+1}$ (patrz rysunek 2b),
- polem powierzchni pod wykresem funkcji kwadratowej, której wykres przechodzi przez punkty $\bigl(x_i, f(x_i)\bigr)$, $\Bigl(\frac{x_i+x_{i+1}}{2}, f\bigl(\frac{x_i+x_{i+1}}{2}\bigr)\Bigr)$ oraz $\bigl(x_{i+1}, f(x_{i+1})\bigr)$, na przedziale $[x_i, x_{i+1}]$ (patrz rysunek 2c).
 Rysunek 2a. Metoda prostokątów |
 Rysunek 2b. Metoda trapezów |
 Rysunek 2c. Metoda Simpsona |
O ile dwie pierwsze metody są raczej dość intuicyjne, o tyle ostatnia (zwana \emph{metodą Simpsona}) wymaga pewnego dodatkowego komentarza.
Skąd wiadomo, jak wygląda wykres funkcji kwadratowej, który przechodzi przez wskazane punkty? Okazuje się, że istnieje co najwyżej jeden wielomian stopnia $k$ przechodzący przez $k+1$ różnych (względem pierwszej współrzędnej) punktów. Jeśli więc wartości $x_i$ oraz $x_{i+1}$ są różne (dlaczego to wystarczy?), to istnieje \emph{co najwyżej jedna} funkcja kwadratowa, której wykres przechodzi przez punkty $\bigl(x_i, f(x_i)\bigr)$, $\Bigl(\frac{x_i+x_{i+1}}{2}, f\bigl(\frac{x_i+x_{i+1}}{2}\bigr)\Bigr)$ oraz $\bigl(x_{i+1}, f(x_{i+1})\bigr)$. Taka funkcja nie istnieje jednak, jeśli trzy badane punkty leżą na jednej prostej.
Pewne matematyczne przekształcenia wskazują, że pole powierzchni pod parabolą przechodzącą przez określone wyżej punkty, na przedziale $[x_i, x_{i+1}]$, wyraża się wzorem $$\frac{x_{i+1}-x_i}{6}\Bigl(f(x_i)+f(x_{i+1}) + 4f\Bigl(\frac{x_{i}+x_{i+1}}{2}\Bigr)\Bigr).$$ Gdy przyjrzymy się temu wzorowi, okaże się, że jeśli punkty $\bigl(x_i, f(x_i)\bigr)$, $\Bigl(\frac{x_i+x_{i+1}}{2}, f\bigl(\frac{x_i+x_{i+1}}{2}\bigr)\Bigr)$ oraz $\bigl(x_{i+1}, f(x_{i+1})\bigr)$ leżą na jednej prostej, to obliczone pole jest równoważne polu obliczonemu metodą trapezów. Nie musimy się więc przejmować tym przypadkiem.
Optymalizacja
Celem tego artykułu jest implementacja kilku funkcji w języku C. Zastosowanie powyższych rozważań wprost spowodowałoby, że wartość funkcji $f$ byłaby obliczana wielokrotnie w tych samych punktach, co wymagałoby więcej mocy obliczeniowej niż to konieczne. Spróbujmy więc zoptymalizować obliczenia na poziomie sumowania pól powierzchni. Jeśli przez $P(a, b)$ oznaczymy właściwe pole powierzchni pod wykresem funkcji $f$ na przedziale $[a, b]$, to w przypadku metody prostokątów otrzymujemy $$ \begin{array}{rcl} P(a, b) & \approx & \sum_{i=0}^{n-1} (x_{i+1} – x_i)\cdot f\Bigl(\frac{x_{i+1}+x_i}{2}\Bigr)\\ & = & \sum_{i=0}^{n-1} \frac{b – a}{n}\cdot f\Bigl(\frac{x_{i+1}+x_i}{2}\Bigr)\\ & = & \frac{b – a}{n}\cdot\sum_{i=0}^{n-1} f\Bigl(\frac{x_{i+1}+x_i}{2}\Bigr), \end{array} $$ w przypadku metody trapezów otrzymujemy $$ \begin{array}{rcl} P(a, b) & \approx & \sum_{i=0}^{n-1} (x_{i+1} – x_i)\cdot \frac{f(x_i) + f(x_{i+1})}{2}\\ & = & \sum_{i=0}^{n-1} \frac{b – a}{n}\cdot \frac{f(x_i) + f(x_{i+1})}{2}\\ & = & \frac{b – a}{2n}\cdot\sum_{i=0}^{n-1} \bigl(f(x_i) + f(x_{i+1})\bigr)\\ & = & \frac{b – a}{2n}\cdot\bigl( f(x_0) + f(x_n) + 2\cdot\sum_{i=1}^{n-1} f(x_i) \bigr), \end{array} $$ a w przypadku metody Simpsona $$ \begin{array}{rcl} P(a, b) & \approx & \sum_{i=0}^{n-1} \frac{x_{i+1}-x_i}{6}\Bigl(f(x_i)+f(x_{i+1}) + 4f\Bigl(\frac{x_{i}+x_{i+1}}{2}\Bigr)\Bigr)\\ & = & \sum_{i=0}^{n-1} \frac{b-a}{6n}\Bigl(f(x_i)+f(x_{i+1}) + 4f\Bigl(\frac{x_{i}+x_{i+1}}{2}\Bigr)\Bigr)\\ & = & \frac{b – a}{6n}\cdot\sum_{i=0}^{n-1} \Bigl(f(x_i)+f(x_{i+1}) + 4f\Bigl(\frac{x_{i}+x_{i+1}}{2}\Bigr)\Bigr)\\ & = & \frac{b – a}{6n}\cdot\Bigl(f(x_0) + f(x_n) + 2\cdot\sum_{i=1}^{n-1}f(x_i)+ 4\cdot\sum_{i=0}^{n-1}f\Bigl(\frac{x_{i}+x_{i+1}}{2}\Bigr)\Bigr).\\ \end{array}$$
Przykład Niech dana będzie funkcja $f(x) = 1+0.1\cdot\sin{(5x)}\cdot\cos{(3x)}.$ Spróbujmy obliczyć pole pod jej wykresem na przedziale $[0, 10]$, wykorzystując każdą z poznanych metod oraz dzieląc przedział $[0, 10]$ na $5$, $10$, $15$, \dots, $95$ oraz $100$ części. Otrzymane wyniki są następujące:
| $n$ | Metoda przybliżania | ||
|---|---|---|---|
| prostokątów | trapezów | Simpsona | |
| 5 | 10.08866501 | 9.97829056 | 10.05187321 |
| 10 | 9.98090553 | 10.03347683 | 9.99843025 |
| 15 | 10.05642509 | 9.97654533 | 10.02979946 |
| 20 | 10.03069878 | 10.00719261 | 10.02286148 |
| 25 | 10.02630901 | 10.01367569 | 10.02209663 |
| 30 | 10.02459717 | 10.01648712 | 10.02189255 |
| 35 | 10.02371883 | 10.01801109 | 10.02181721 |
| 40 | 10.02320099 | 10.01894379 | 10.02178288 |
| 45 | 10.02286720 | 10.01956081 | 10.02176476 |
| 50 | 10.02263641 | 10.01999187 | 10.02175617 |
| 55 | 10.02247334 | 10.02030563 | 10.02175045 |
| 60 | 10.02234840 | 10.02053833 | 10.02174568 |
| 65 | 10.02225494 | 10.02072144 | 10.02174473 |
| 70 | 10.02218056 | 10.02086449 | 10.02174473 |
| 75 | 10.02212429 | 10.02097797 | 10.02174282 |
| 80 | 10.02207565 | 10.02107430 | 10.02173901 |
| 85 | 10.02203560 | 10.02114868 | 10.02173996 |
| 90 | 10.02200031 | 10.02121544 | 10.02173901 |
| 95 | 10.02197742 | 10.02126789 | 10.02173805 |
| 100 | 10.02195358 | 10.02131653 | 10.02173901 |
Kod źródłowy programu wykonującego obliczenia
#include <stdio.h>
#include <math.h>
float f(float x){
return 1 + 0.1*sin(5*x)*cos(3*x);
}
float approxRect(float a, float b, int n, float (*f)(float)){
int i;
float range = (b-a)/n;
float res = 0;
float x;
for(i=0; i<n; i++){
x = a + range*i + range/2;
res = res + (*f)(x);
}
return res * range;
}
float approxTrap(float a, float b, int n, float (*f)(float)){
int i;
float range = (b-a)/n;
float res = 0;
float x;
res = res + (*f)(a) + (*f)(b);
for(i=1; i<n; i++){
x = a + range*i;
res = res + 2 * (*f)(x);
}
return (res * range)/2;
}
float approxSimpson(float a, float b, int n, float (*f)(float)){
int i;
float range = (b-a)/n;
float res = 0;
float xi, xii;
res = res + (*f)(a) + (*f)(b);
for(i=0; i<n; i++){
xi = a + range*i;
xii = xi + range;
if(i>0) res = res + 2*(*f)(xi);
res = res + 4*(*f)((xi+xii)/2);
}
return (res * range)/6;
}
int main(){
int n;
for(n=5; n<=100; n+=5){
printf("%3d %12.8f %12.8f %12.8f\n",
n,
approxRect(0, 10, n, &f),
approxTrap(0, 10, n, &f),
approxSimpson(0, 10, n, &f));
}
return 0;
}
* Wartość pola powierzchni pod wykresem funkcji $f$ na zadanym przedziale $[a, b]$ to nic innego jak całka oznaczona z funkcji $f$ na tym przedziale.
** Bardziej wnikliwi obserwatorzy zadadzą z pewnością pytanie, dlaczego możemy umieścić punkty graniczne w dwóch sąsiadujących przedziałach jednocześnie. Jest tak dlatego, że pole powierzchni pod wykresem na przedziale o długości 0 jest równe 0.