Ekonomia to nauka niesamowicie ,,młoda”. W porównaniu z matematyką, chemią, historią, czy filozofią można powiedzieć, że dopiero stawia pierwsze kroki. Narodziny ekonomii przypadają na rok 1776. Warto jednak zwrócić uwagę, że ekonomia zaczynała jako nauka społeczna i używanie w niej jakichkolwiek równań matematycznych było uważane początkowo za duże faux pas. Dzisiaj, pomimo tego, że ekonomia wciąż jest nauką społeczną, to korzysta bardzo intensywnie z aparatu matematycznego. Nagroda im. Alfreda Nobla w dziedzinie nauk ekonomicznych prawie co roku trafia do ekonomistów pracujących nad tematami takimi jak teoria gier, ekonometria, badania operacyjne, teoria równowagi ogólnej lub wzrostu gospodarczego. 1 Są to zagadnienia nierozerwalnie związane z modelowaniem matematycznym. Za pomocą funkcji, zbiorów i równań ekonomiści opisują zachowania konsumentów, producentów, konkurentów, a nawet całej gospodarki i z pomocą tych modeli starają się przewidywać przyszłość.
Zanim jednak zaczniemy używać funkcji i zbiorów, zastanówmy się chwilę nad tym, czym jest model. Aby dokładniej zrozumieć istotę modelu matematycznego (w szczególności takiego używanego w ekonomii), musimy na chwilę oderwać się od monitora i wyruszyć na wycieczkę – najlepiej rowerową. Chwytamy w rękę plecak i ruszamy w trasę. Niestety, w środku lasu, gdzie brak sygnału GPS i sieci komórkowej, zgubiliśmy drogę. Na całe szczęście po lekcji geografii zostały nam w torbie jeszcze jakieś mapy. Pierwsza z nich to mapa samochodowa. Łatwo się domyślić, że naszej ścieżki rowerowej na niej nie znajdziemy – trasy te nie są potrzebne kierowcom samochodów. Mamy również mapę rowerową – są na niej wszystkie informacje dla nas istotne – drogi i ścieżki rowerowe, kontrapasy, miejsca warte zobaczenia. Z pewnością nie znajdziemy tutaj informacji dotyczących parkingów na autostradach, o klasie gleby lub też liczby mieszkańców danej miejscowości – dane te nie są dla rowerzystów przydatne. Popatrzmy jeszcze na prawy dolny róg mapy – jaką mamy skalę? Prawdopodobnie \(1:2000\) lub \(1:10000\). Dla mapy Polski skala byłaby prawdopodobnie bliżej \(1:500000\). Nie korzystamy nigdy z mapy \(1:1\) lub \(1:2\), bo byłoby to niewygodne i do niczego taka mapa by się nam nie przydała.
Model ekonomiczny możemy potraktować właśnie jako taką mapę gospodarki – nie będzie nam potrzebne odwzorowanie w skali \(1:1\), bo byłoby ono nieprzydatne i bardzo niewygodne w użyciu. Jeżeli tworzymy model, to przyglądamy się tylko pewnemu fragmentowi rzeczywistości, który nas interesuje i upraszczamy całą resztę. W ten sposób model stanie się przejrzysty, łatwo będzie z niego korzystać i używać do prognozowania przyszłości. Firma produkująca samochody, która będzie zainteresowana maksymalizacją swoich zysków, nie będzie potrzebowała informacji o popycie na ziemniaki. Musi ona posiadać informacje o kosztach swojej produkcji, o tym, jakie podatki zapłaci i ile towaru będą chcieli kupić konsumenci. Ekonomiści pracujący w tej firmie zbudują więc matematyczny model, który odpowie na pytania ile towarów wyprodukować w następnym okresie, jaką cenę ustalić (żeby zarobić jak najwięcej, ale żeby konkurencja nie odebrała nam klientów) i jakie koszty trzeba będzie ponieść.
Skoro wiemy już, czym jest model, to spróbujmy odpowiedzieć na pytanie – jak stworzyć matematyczny opis człowieka. Oczywiście nie będziemy interesowali się obwodem jego głowy, czy rozmiarem stopy, a raczej tym, jak się zachowuje. Do takiego opisu potrzebować będziemy funkcji i to najlepiej funkcji wieloargumentowej. Zamiast odwzorowania \(f(x)=y\), gdzie \(x\) i \(y\) to pewne liczby rzeczywiste, częściej będzie nas interesowało odwzorowanie \(f(x_1,x_2,\ldots,x_n )=y\). Łatwo zauważyć, że nie przyporządkowujemy tutaj jednej liczbie \(x\) jednej liczby \(y\), tylko pewnemu uporządkowanemu zbiorowi liczb (wektorowi) \(\left(x_1,x_2,x_3,….,x_n\right)\) przyporządkowujemy jedną liczbę \(y\).
Powstaje jednak pytanie, co taka funkcja powinna opisywać? Aby na nie odpowiedzieć, należy sięgnąć do istoty ekonomii i tego, czym ekonomiści się zajmują. Ekonomia bada, jak rozdysponować ograniczone i rzadkie zasoby i dobra w społeczeństwie w taki sposób, aby zwiększać dobrobyt. Nauka ta skupia się w dużej mierze na relacjach pomiędzy kupującym a sprzedającym oraz na analizie gospodarki. Innymi słowy – będziemy chcieli opisać człowieka, który ma pewne zasoby (czyli na przykład dochód) i chce je wymienić na towary w taki sposób, aby być jak najbardziej zadowolonym. Naszą funkcję możemy więc traktować jako pewne odwzorowanie opisujące zadowolenie naszego konsumenta. Ekonomiści taką funkcję nazywają funkcją użyteczności konsumenta i zazwyczaj oznaczają przez \(u(x_1,x_2,\ldots,x_n)\).
Wiemy już, co nasza funkcja ma opisywać. Zastanówmy się więc, w jaki sposób funkcja może opisywać zadowolenie konsumenta. Argument \(x_i\) możemy utożsamiać z pewnym kupowanym w sklepie towarem. Wchodząc do sklepu zazwyczaj bierzemy koszyk i do niego wrzucamy produkty, które chcemy kupić. Potraktujmy wektor \(x=(x_1,x_2,\ldots,x_n)\) jako koszyk, do którego dodajemy towary. Dla uproszczenia załóżmy, że chcemy kupić w sklepie dwie rzeczy – napój \((x_1)\) i czekoladę \((x_2)\). Oczywiście od razu powinno nam zaświtać, że będą nas interesowały tylko liczby nieujemne. Nie mogę w sklepie kupić \((-3)\) czekolad. Dla uproszczenia jednak, ze względów obliczeniowych bardzo często przyjmuje się, że towary, które chcemy kupić, są nieskończenie podzielne. Przy tym założeniu, każdy z naszych argumentów będzie należał do zbioru liczb nieujemnych \(\mathbb{R}_+=\left\langle 0,+\infty\right)\). Oczywiście ktoś mógłby zacząć się kłócić, że w sklepie nie można kupić \(\sqrt{2}\) tabliczek czekolady, ale jest to po prostu jedno z uproszczeń, o których wcześniej pisaliśmy. Dziedziną naszej funkcji będzie w tym szczególnym przypadku zbiór \(\mathbb{R}^2_+\), a ogólniej (przy koszyku \(n\)-elementowym) zbiór \(\mathbb{R}^n_+\).
Skoro ustaliliśmy dziedzinę, to możemy przejść do własności funkcji użyteczności. Przede wszystkim, jeżeli mamy dwa koszyki towarów \(x=(x_1, x_2)\) oraz \(y=(y_1,y_2)\) i wiemy, że koszyk \(x\) jest dla nas lepszy niż koszyk \(y\) (będziemy z jego wyboru bardziej zadowoleni), to dla funkcji użyteczności będzie to oznaczało, że \(u(x_1,x_2)> u(y_1,y_2)\), a jeżeli koszyki te są dla nas tak samo interesujące, to \(u(x_1,x_2)=u(y_1,y_2)\). Możemy od razu zauważyć, że raczej nie będą nas interesowały funkcje różnowartościowe (czyli iniekcje). Dopuszczamy przecież możliwość, że różne kombinacje towarów mogą dać nam takie samo zadowolenie.2
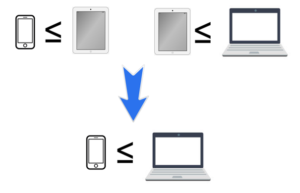
Na początku wspomnimy o dwóch własnościach, które spełnia każda funkcja, ale w szczególności własności te są potrzebne przy opisywaniu zachowania konsumenta. Uprośćmy na chwilę naszą sytuację i załóżmy, że wybieramy tylko jeden towar – sprzęt elektroniczny. Po pierwsze, interesuje nas spójność odwzorowania (zwana też zupełnością). Z ekonomicznego punktu widzenia oznacza to tyle, że stojąc przed wyborem pomiędzy dwoma towarami – telefonem i tabletem – będziemy w stanie podjąć decyzję. Są tylko trzy możliwości – możemy preferować i wybrać tablet lub możemy preferować komórkę. Trzecia możliwość, to sytuacja, w której tablet i komórka są dla nas tak samo interesujące. Jeżeli potraktujemy teraz komórkę jako towar \(x\), a tablet jako \(y\), to możemy powiedzieć, że dla dwóch dowolnych wektorów z dziedziny dostajemy \(u(x)\geq u(y)\) lub też \(u(y)\geq u(x)\)
Zupełność preferencji
Rysunek 1
Ponadto chcemy również, aby nasza funkcja była przechodnia. Co to dokładnie oznacza? Mamy do wyboru tablet lub telefon – załóżmy, że bardziej zainteresowani jesteśmy tabletem. Po chwili jednak, mając tablet w ręku, zauważyliśmy ciekawy laptop. W tym momencie, wybierając pomiędzy laptopem a tabletem, preferujemy laptop (zob. Rysunek 2).
Przechodniość oznacza, że gdybyśmy zostali postawieni przed wyborem pomiędzy laptopem, a telefonem – wciąż wybralibyśmy laptop. W języku matematycznym oznacza to, że jeżeli mamy trzy wektory \(x, y, z \in \mathbb{R}^n_+\) i dla funkcji użyteczności zachodzą nierówności \(u(x)\geq u(y)\) oraz \(u(y) \geq u(z)\), to wiemy, że na pewno zajdzie również nierówność \(u(x)\geq u(z)\). O konsumencie, którego zachowanie jest spójne i przechodnie, mówimy że zachowuje się w sposób racjonalny.3
Przechodniość preferencji
Rysunek 2
Zacznijmy od ciągłości funkcji. Intuicyjnie funkcję ciągłą określoną na zbiorze \(\mathbb{R}\) możemy scharakteryzować jako funkcję, której wykresem jest ciągła linia, tj. możemy wykres tej funkcji narysować bez odrywania długopisu od kartki. Inaczej możemy powiedzieć, że funkcja jest ciągła, gdy mała zmiana argumentu powoduje niewielką zmianę wartości funkcji. Od konsumentów wymagamy, żeby zachowywali się właśnie w sposób ciągły. Jeżeli wybieramy pomiędzy dwoma koszykami towarów \(x, y\in \mathbb{R}^n_+\) i wolimy koszyk \(x\) od koszyka \(y\), tzn. \(u(x)> u(y)\), to oczekujemy, że zmieniając niewiele w tych koszykach (na przykład dodając do każdego po jednym towarze), nierówność ta zostanie zachowana. Okazuje się, że przy spełnieniu pewnych warunków, taka ciągła funkcja użyteczności zawsze będzie istniała, o czym mówi następujące twierdzenie:
Twierdzenie 1
Jeżeli przestrzeń towarów \(X=\mathbb{R}^n_+\) i relacja preferencji konsumenta jest ciągła w \(X\), to istnieje ciągła funkcja użyteczności \(u:X\rightarrow \mathbb{R}^1\) związana z tą relacją preferencji.
Jak już wcześniej powiedzieliśmy – oczekujemy, że konsument będzie się zachowywał w sposób ciągły, a dziedzina będzie zbiorem \(X=\mathbb{R}^n_+\). Powyższe twierdzenie wskazuje, że wystarczą tylko te dwa założenia, abyśmy zawsze byli w stanie znaleźć pewną ciągłą funkcję użyteczności, za pomocą której uda nam się opisać preferencje konsumenta.
Wyobraźmy teraz sobie, że udało nam się wygrać nagrodę w konkursie organizowanym przez księgarnię. Jako wygraną możemy wybrać – czy chcemy jedną dowolną książkę z tejże księgarni, czy chcemy takich książek dziesięć. W obu przypadkach za nagrodę nie musimy oczywiście nic płacić, a książki sa dowolne. Myślę, że każdy z nas wybrałby jako nagrodę dziesięć książek, a nie jedną:
Zachłanność konsumenta
Rysunek 3
Człowiek zazwyczaj jest zachłanny i im ma więcej, tym jest bardziej zadowolony – zjawisko to nazywamy w ekonomii zjawiskiem niedosytu. Jak zwykle zastanówmy się, co to dla nas będzie oznaczało z matematycznego punktu widzenia. Weźmy dwa wektory \(x=(x_1,x_2)\) oraz \(y=(y_1,y_2)\) takie, że \(x_1 > y_1\) oraz \(x_2 > y_2\). Koszyk \(x\), w którym mamy więcej towarów (wracając do naszego wcześniejszego przykładu – więcej czekolad i napojów), ma dla nas wyższą użyteczność. O tym, jaki ma to wpływ na funkcję użyteczności, mówi poniższe twierdzenie:
Twierdzenie 2
Jeżeli dla towarów z przestrzeni \(\mathbb{R}^n_+\) i dla preferencji konsumenta spełnione jest zjawisko niedosytu, to każda funkcja użyteczności związana z preferencjami konsumenta jest rosnąca.
Oznacza to oczywiście, że jeżeli konsument będzie preferował zawsze koszyk, w którym jest więcej towarów, to wtedy dla \(x_1 > y_1\) oraz \(x_2 > y_2\) mamy również \(u(x_1,x_2) > u(y_1,y_2)\). Funkcja, która opisuje preferencje konsumenta zawsze będzie funkcją rosnącą – im wyższe wartości argumentów, tym wyższa powinna być wartość funkcji.
Kolejna własność, której będziemy wymagać od funkcji użyteczności, to jej silna wklęsłość.4
Powiedzieliśmy przed chwilą, że człowiek jest zachłanny – jego zadowolenie będzie tym wyższe, im więcej będzie posiadał. Przyjrzyjmy się jeszcze na chwilę temu, jak mocno rośnie nasze zadowolenie w różnych sytuacjach. Jeżeli nie mieliśmy ani jednej tabliczki czekolady i dostaliśmy jedną tabliczkę czekolady, to wzrost naszego zadowolenia jest bardzo duży. W sytuacji, gdy mieliśmy już tabliczkę czekolady i dostaliśmy drugą, to nasze zadowolenie wzrasta, ale już nieco mniej, niż w pierwszym przypadku. Gdybyśmy natomiast mieli już dziesięć tabliczek czekolady i dostalibyśmy jedenastą, to przyrost zadowolenia byłby zdecydowanie mniejszy, niż w dwóch pierwszych przypadkach. Matematycznie wymagamy, aby funkcja użyteczności była silnie wklęsła na swojej dziedzinie, a więc aby dla dwóch dowolnych punktów \(x,y\in \mathbb{R}^n_+\) oraz dla dwóch dowolnych liczb rzeczywistych \(\alpha, \beta \in \left\langle 0,1\right\rangle \) takich, że \(\alpha + \beta =1\) spełniała warunek:
\[f(\alpha x + \beta y) \geq \alpha f(x) + \beta f(y).\]
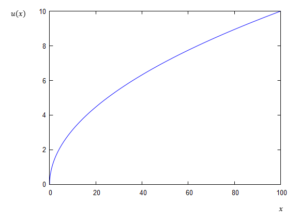
Przedstawiliśmy kilka bardzo podstawowych własności funkcji, których używa się często przy modelowaniu zachowania konsumentów. Zastanówmy się teraz, jak mogłaby wyglądać funkcja, której dziedziną byłby zbiór liczb rzeczywistych nieujemnych i która byłaby funkcją ciągłą, rosnącą i silnie wklęsłą. Dla uproszczenia zacznijmy od przykładu, gdzie \(x\in\mathbb{R}_+\), czyli mamy do czynienia z funkcją jednoargumentową. Jako przykład takiej funkcji możemy przedstawić odwzorowanie \(u(x)=\sqrt{x}\) lub też bardziej ogólnie \(u(x)=\sqrt[n]{x}\), przy założeniu, że \(x\in \mathbb{R}_+\) oraz \(n> 1\). (zob. Rysunek 4)
\(u(x)=\sqrt{x}\)
Rysunek 4
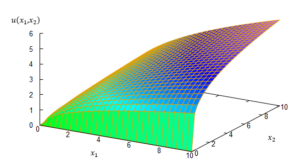
Przechodząc na funkcję dwuargumentową \(x\in \mathbb{R}^2_+\) – jako przykład możemy podać funkcję postaci
\[u(x_1,x_2)=x_1^{\frac{1}{2}} x_2^{\frac{1}{4}}\]
lub bardziej ogólnie
\[u(x_1,x_2)= x_1^{\alpha} x_2^{\beta},\]
gdzie \(\alpha, \beta > 0\) oraz \(\alpha + \beta \leq 1\). (zob. Rysunek 5)
\(u(x_1,x_2)=x_1^{\frac{1}{2}} x_2^{\frac{1}{4}}\)
Rysunek 5
Funkcja ta jest często stosowana w ekonomii zarówno przy opisie zachowań konsumentów, jak i przy opisie produkcji w przedsiębiorstwie i nazywana jest funkcją Cobba-Douglasa. W największym uogólnieniu, gdy \(x\in \mathbb{R}^n_+\), funkcja ta będzie miała postać:
\[u(x_1,x_2,\ldots,x_n)=\prod_{i=1}^{n} x_i^{\alpha_i}=x_1^{\alpha_1}\cdot x_2^{\alpha_2}\cdot \ldots \cdot x_n^{\alpha_n},\]
gdzie \(\alpha_1, \alpha_2, \ldots, \alpha_n > 0\) oraz \(\sum_{i=1}^{n} \alpha_i\leq 1\).
Zatrzymajmy się przez chwilę przy funkcji dwuargumentowej \(u(x_1,x_2)=x_1^{\frac{1}{2}} x_2^{\frac{1}{4}}\). Załóżmy, że zachowanie pewnego konsumenta jest opisane właśnie za pomocą takiej funkcji użyteczności. W jaki sposób możemy tę informację wykorzystać? Po pierwsze łatwiej jest nam porównywać koszyki konsumenta. Wróćmy do przykładu, gdzie towarem \(x_1\) były tabliczki czekolady, a towarem \(x_2\) napoje. Oczywiście w tym momencie wiemy już, że nasz konsument będzie preferował koszyk \((4,9)\) nad koszyk \((1,4)\) – użyteczności dla tych koszyków byłyby odpowiednio równe:
\[
u(4,9)=\sqrt{4}\cdot \sqrt[4]{9}=2\sqrt{3}\approx 3,46,\]
\[u(1,4)=\sqrt{1}\cdot \sqrt[4]{4}=\sqrt{2}\approx 1,41.\]
Problem pojawia się jednak, gdy mamy przewidzieć, czy nasz konsument wybierze koszyk \((25,16)\) czy też \((9,36)\). W drugim z tych koszyków pierwszego towaru jest mniej, ale za to drugiego towaru więcej. Dzięki funkcji użyteczności jesteśmy w stanie bardzo szybko wywnioskować, jakiego wyboru dokona konsument:
\[u(25,16)=\sqrt{25}\cdot \sqrt[4]{16}=5\cdot 2 = 10,\]
\[u(9,36)=\sqrt{9}\cdot \sqrt[4]{36}=3\sqrt{6}\approx 7,35.\]
Użyteczność koszyka \((25,16)\) jest większa, więc to ten koszyk zostanie wybrany przez konsumenta.
Po drugie, łatwo ocenić nam, jak zmieniać się będzie zadowolenie konsumenta, przy zmianach ilości towarów. Załóżmy, że jesteśmy właścicielem sklepu i chcemy zachęcić klientów, żeby kupowali u nas produkty. Wiemy, że przeciętnie podczas dużych zakupów klienci kupują jedną czekoladę oraz cztery napoje, a ich preferencje opisane są za pomocą funkcji użyteczności \(u(x_1,x_2)=x_1^{\frac{1}{2}} x_2^{\frac{1}{4}}\). Czy nasi klienci bardziej ucieszą się, jeżeli damy im w promocji dodatkową tabliczkę czekolady, czy też będą woleli dodatkowy napój? Wiemy, że \(u(1,4)\approx 1,41\). Zobaczmy, jak będzie kształtowało się zadowolenie konsumenta, przy koszykach \((2,4)\) oraz \((1,5)\)
\[u(2,4)=\sqrt{2}\cdot \sqrt[4]{4}=2,\]
\[u(1,5)=\sqrt{1}\cdot \sqrt[4]{5}=\sqrt[4]{5}\approx 1,5.\]
Od razu możemy zauważyć, że użyteczność wzrosła w obu przypadkach, jednak \(u(2,4) > u(1,5)\). W promocji powinna się więc pojawić dodatkowa czekolada, a nie napój.
Przedstawione własności pojawiają się często w modelach ekonomicznych. Tak naprawdę jednak zahaczyliśmy tylko o szczyt ogromnej góry lodowej – do naszych rozważań nie wprowadziliśmy w ogóle dochodów i cen – dopiero wtedy cały problem zaczyna być naprawdę ciekawy. To niezwykle mocno ogranicza wybór (jak i zachłanność) konsumenta. Ponadto skupiliśmy się na jednym konsumencie. Co stanie się, gdy będziemy mieli modelować zachowanie całego społeczeństwa? Czy jesteśmy w stanie zrobić to za pomocą jednej funkcji użyteczności, czy trzeba wykorzystać takich funkcji wiele? A co stanie się, gdy do modelu dodamy pracę konsumenta i możliwość brania kredytu? Takich pytań jest wiele, a w poszukiwaniu odpowiedzi ekonomistom pomaga każdego dnia matematyka. Pozwala ona formułować problemy w sposób precyzyjny, a za pomocą narzędzi matematycznych ekonomiści są w stanie przewidywać przyszłość i modelować zmiany zachodzące w gospodarce. Prawie jak wróżka z magiczną kulą…
Przypisy
- Warto zaznaczyć, że nagroda ta jako jedyna nie pochodzi z funduszy pozostawionych przez Alfreda Nobla, a została ustanowiona w roku 1968 przez Bank Szwecji.
- Na przykład 3 batoniki i jeden napój mogą być dla nas tak samo atrakcyjne jak 2 batoniki i 2 napoje. Wtedy wartości funkcji użyteczności dla tych dwóch kombinacji będą sobie równe.
- Oczywiście, możemy nie zgadzać się z tym, że ludzie są racjonalni. Bardzo często nie zachowują się w sposób racjonalny. Małe dziecko w sklepie, jeżeli może wybrać pomiędzy piłką i misiem i wybierze misia, a następnie będzie miało wybrać pomiędzy misiem a grą i wybierze grę, to postawione przed dylematem, czy woli piłkę czy grę, może odpowiedzieć, że woli oczywiście piłkę. Jak jednak wspominaliśmy na początku artykułu, nasz model upraszcza nieco rzeczywistość i dlatego będziemy zakładać, że konsument zachowuje się w sposób racjonalny. Nie oznacza to oczywiście, że jest to założenie przyjmowane w każdym modelu. Bardzo często w najnowszych modelach ekonomicznych zakłada się, że konsumenci nie zawsze zachowują się w sposób racjonalny. Takimi tematami bardzo często zajmuje się na przykład teoria gier.
- Tak naprawdę, wystarczy często że funkcja jest wklęsła, ale zakładając silną wklęsłość funkcji użyteczności, dostajemy więcej interesujących twierdzeń ekonomicznych.
Artykuł został przygotowany przy wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.