Wydawałoby się, że o wielościanach wiemy już wszystko. No bo jak moglibyśmy nie znać na wylot tych namacalnych obiektów, które od dawien dawna zewsząd otaczają człowieka? Dysponujemy przecież wzorami na wyliczenie objętości wielościanów. Doskonale wiemy, że istnieje (bardzo użyteczna dla każdego ucznia) zależność pomiędzy liczbą ścian ($S$), wierzchołków ($W$) i krawędzi ($K$) wielościanu wypukłego. Jest to tak zwany wzór Eulera, mający postać $S+W-K=2$. Ponadto w szkole uczymy się wyznaczać kąty dwuścienne, wyliczać pole powierzchni bocznej, dowiadujemy się, czym są bryły archimedesowe i platońskie, a także stykamy się z pojęciami ostrosłupa (prawidłowego, ściętego), graniastosłupa (prostego, pochyłego, prawidłowego) oraz prostopadłościanu.
Zapytacie, co więcej musimy wiedzieć o bryłach jako takich, żeby – dajmy na to – narysować ich siatki, bo akurat chcemy zaprojektować nowe wielościenne opakowanie1 na – powiedzmy – kakao. Warto zastanowić się, czy siatka jednoznacznie wyznacza nam kształt wielościanu2. I tu natrafiamy na pierwszą ciekawostkę. Jeśli daną siatkę skleimy do wielościanu wypukłego – będzie on jedynym wielościanem wypukłym możliwym do zrealizowania w wyniku tego sklejenia. Jeżeli natomiast skleimy naszą siatkę do wielościanu niewypukłego, nie umiemy stwierdzić, czy ten wielościan jest jedynym niewypukłym, jaki możemy dostać. Gdy nie jest jedyny, to w znakomitej większości przypadków nie możemy otrzymać tego drugiego poprzez ciągłe przekształcenie (ruch) pierwszego – należałoby rozciąć jedną powierzchnię3, a następnie ponownie złożyć siatkę. ,,W znakomitej większości”, ponieważ dopiero w 1977 roku skonstruowano pierwszą powierzchnię wielościenną, którą można poruszać tak, aby miała istotnie inny kształt od wyjściowego – z tej samej siatki w sposób ciągły dostajemy różne realizacje naszej powierzchni.
Sztywność i deformacje
W wielu sytuacjach możemy zatem powiedzieć, że powierzchnie wielościenne są sztywne. Mamy tu na myśli powierzchnie wielościenne bez żadnych dziur, tzn. nie przypominają one ani amerykańskiego pączka z dziurą (tzw. donata), ani kartonu mleka z uciętym rogiem. Sztywność nie oznacza jednak jedyności realizacji (z tej samej siatki możemy złożyć zarówno powierzchnię wypukłą, jak i niewypukłą; por. applet poniżej). Sztywność mówi nam o braku ciągłego przejścia między dowolnymi dwoma realizacjami.
Interesują nas ciągłe przejścia w przestrzeni trójwymiarowej nie zmieniające odległości pomiędzy dowolnymi dwoma punktami na powierzchni4 (tzw. ruchy izometryczne). Ponadto, zakładamy, że poruszanie powierzchnią wielościenną nie rozrywa jej ani nie rozciąga (kształt, wymiary i płaskość ścian są zachowane). Przykładem na płaszczyźnie jest sztandarowe ,,kopnięcie” prostokąta do równoległoboku. Długości krawędzi w wyniku deformacji nie zmieniają się, zatem jest to ruch izometryczny. Trywialnym przykładem w przestrzeni jest na przykład przesunięcie lub obrót. Natomiast przesuwanie górnego wierzchołka czworościanu w płaszczyźnie równoległej do podstawy nie jest ruchem izometrycznym – zachowuje wprawdzie objętość, ale odległości mierzone po ścianach zmieniają się, a w związku z tym wymiary ścian nie są zachowane.
Trochę historii
W 1813 roku francuski matematyk Augustin Louis Cauchy udowodnił, że wielościany wypukłe są sztywne, a więc jedyny ciągły ruch jaki mogą wykonać to tzw. ruch sztywny, czyli przesunięcie lub obrót. A co z wielościanami niewypukłymi? No właśnie, tu zaczyna się robić ciekawiej. Dopiero w 1974 roku matematyk Herman Gluck z Uniwersytetu Pensylwanii stwierdził, że istnieją wielościany (oczywiście niewypukłe – spróbujcie odpowiedzieć dlaczego?), które nie są sztywne, ale nie wiadomo, jak wyglądają. Typowa sytuacja, w której często znajduje się matematyk – umie on pokazać, że jakiś obiekt istnieje, ale nie wie, jaką ma dokładnie postać. Pikanterii dodaje fakt, iż Gluck pokazał coś jeszcze – takie poruszające się powierzchnie wielościenne są dla przestrzeni, w której żyją, jak kropla wody dla oceanu. Mówiąc prościej – owszem, jest szansa znaleźć taki wielościan (bądź wielościany), ale szansa ta jest raczej marna.
Jakże wielką radością dla Roberta Connelly’ego z Uniwersytetu Cornella musiała zatem być udana konstrukcja w 1977 roku tzw. fleksora – czyli wielościanu, który może się poruszać zmieniając swój kształt. Jego model posiada 18 ścian, 11 wierzchołków i 27 krawędzi. Wzorując się na pomyśle fleksora Connelly’ego, Klaus Steffen utworzył fleksor o 14 ścianach, 9 wierzchołkach i 21 krawędziach – jego siatkę przedstawiamy na rysunku poniżej, aby każdy niedowiarek mógł skleić taki model i zobaczyć na własne oczy, co się tam właściwie dzieje. Zalecanym materiałem byłby jednak metal, a nie papier, gdyż przy ruszaniu naszą powierzchnią każda ściana z osobna musi pozostać sztywna (tj. przystająca do siebie). I od razu uprzedzamy, że ruch ten nie będzie spektakularny – raczej subtelny.
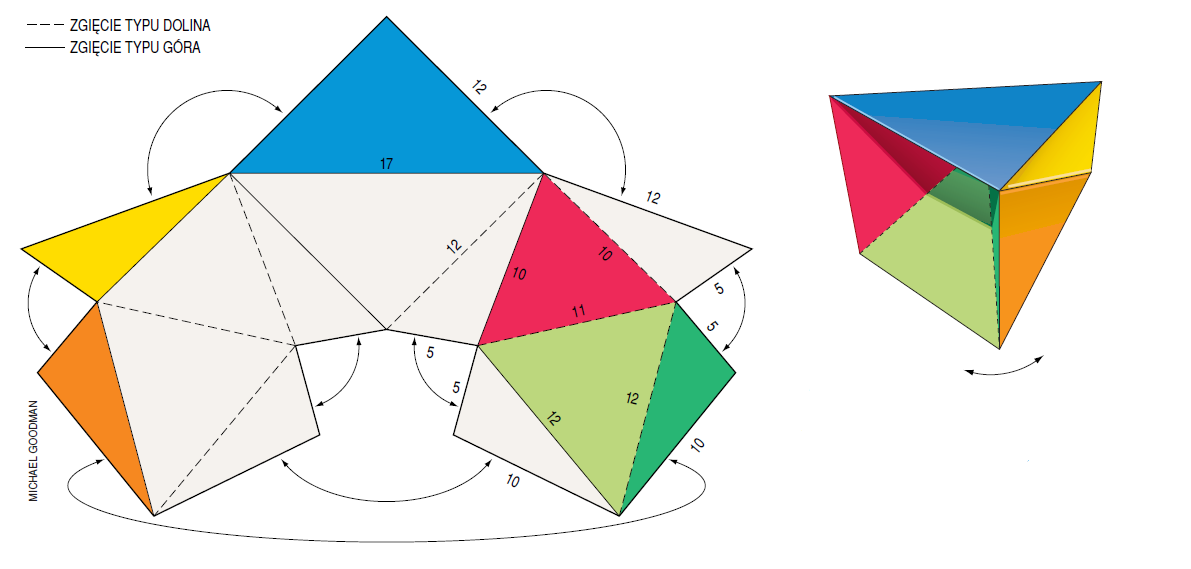
Siatka flexora Steffena. Rysunek autorstwa Michaela Goodmana pochodzący z artykułu Iana Stewarta «The Bellows Conjecture» (Scientific American, July 1998)
Co ciekawe, w 1995 roku rosyjski matematyk I. G. Maksimow pokazał, że wszystkie powierzchnie wielościenne bez dziur o trójkątnych ścianach i mające mniej niż 9 wierzchołków, są sztywne. Z tego względu ruchomy wielościan Steffena powinien wydawać się nam jeszcze bardziej wyjątkowy – znaleźliśmy bowiem fleksor o najmniejszej liczbie wierzchołków!
Objętość wielościanu
Dość naturalnie nasuwa się nam teraz ważne pytanie – oczywiście w kontekście opakowania na kakao – czy taka ruszająca się powierzchnia wielościenna ogranicza nam tę samą objętość? Jeśli ktoś jeszcze nie widzi istoty tego pytania, sformułujmy je inaczej. Czy ruszanie takim wielościennym opakowaniem nie zmniejszy nam objętości i w konsekwencji zmieści się w nim mniej kakao? Jest to dość zasadnicza kwestia dla każdego łasucha! Problem ten został rozwiązany dopiero w 1997 roku przez trzech matematyków, m.in. przez wspomnianego już wcześniej Roberta Connelly’ego. Łasuchy nie mają powodu ani do płaczu, ani do radości – okazuje się, że ruszające się fleksory zachowują swoją objętość (jest to tzw. twierdzenie o miechu). Choć przyznacie, że twierdzenie o kakao brzmiałoby dużo lepiej i pasowałoby do znanego każdemu matematykowi twierdzenia o naleśnikach czy też twierdzenia o kanapce…
Mamy za sobą ruszanie powierzchnią wielościenną bez naruszania kształtów jej ścian. Zastanówmy się teraz nad deformacjami powierzchni – czyli niejako podziałem niektórych ścian na mniejsze kawałki i takie ciągnięcie tylko za niektóre z tych kawałków, aby nie rozerwać naszej powierzchni. Spójrzmy na poniższy przykład, aby lepiej zobrazować sobie tę sytuację. Przy słodkościach będąc – wartościowym przykładem będzie tzw. kostka Milki. Nie chodzi nam jednak (niestety) o fioletową czekoladę, tylko o zdeformowaną powierzchnię sześcianu (kostki). Nazwa pochodzi od nazwiska Anatolija Milki – pomysłodawcy tej deformacji.
Kwadrat Milki
Zanim spojrzymy na kostkę trój-wymiarową zanalizujmy analogiczną sytuację na płaszczyźnie. Weźmy kwadrat jednostkowy i podzielmy każdą jego krawędź na odcinki długości $\varepsilon$, $1-2\varepsilon$ i $\varepsilon$. Zakładając, że te kawałki krawędzi są wykonane na przykład z metalowych drążków połączonych ze sobą, możemy wysunąć odcinki długości $1-2\varepsilon$ od środka kwadratu tak, aby sąsiednie krawędzie $\varepsilon$ stały się współliniowe, co przedstawione jest na rysunku poniżej. Naszym zadaniem na płaszczyźnie jest zmaksymalizowanie pola powierzchni. Pole powierzchni wielokąta po deformacji wynosi u nas
\[P(\varepsilon)=4\cdot\frac{1}{2}(\varepsilon\sqrt{2})^2+2\cdot(1-2\varepsilon)\cdot\varepsilon\sqrt{2}+(1-2\varepsilon)(2\cdot\varepsilon\sqrt{2}+1-2\varepsilon),\]
a po uporządkowaniu wyrażeń
\[P(\varepsilon)=(8-8\sqrt{2})\varepsilon^2+(4\sqrt{2}-4)\varepsilon+1.\]
Największe zwiększenie pola powierzchni dostaniemy dla naszej deformacji w przypadku, gdy $\varepsilon=0,25$, ponieważ pochodna $P'(\varepsilon)=(16-16\sqrt{2})\varepsilon+4\sqrt{2}-4$ zeruje się właśnie dla $\varepsilon=0,25$.
Kostka Milki
Jeśli konstrukcja kwadratu którego „łamanie” zwiększa pole powierzchni jest już jasna, przejdźmy jeden wymiar wyżej – do konstrukcji Igora Paka z Uniwersytetu Kalifornijskiego bazującej na deformacji Anatolija Milki. W skrócie polega ona na podziale powierzchni każdej ściany sześcianu (dla uproszczenia obliczeń – jednostkowego, czyli o długości krawędzi równej jednej jednostce) na cztery małe kwadraty o boku długości $\varepsilon$ (gdzie $\varepsilon$ jest dodatnią stałą mniejszą niż $0{,}5$), cztery prostokąty oraz jeden duży kwadrat i późniejszym ,,wysunięciu” tego ostatniego od środka ciężkości o $\varepsilon(\sqrt{2}-1)$ jednostek. Każde naroże sześcianu przekształci się wtedy w powierzchnię boczną ostrosłupa o ścianach bocznych będącymi trójkątami prostokątnymi. Animacja pokazująca uzyskaną bryłę dla różnych wartości $\varepsilon$ prezentujemy poniżej.
Obliczmy objętość tak powstałej bryły. W samym środku mamy sześcian $S$ o długości krawędzi równej $(1-2\varepsilon)$ – jego objętość wynosi $(1-2\varepsilon)^3$. Do każdej ściany $S$ jest ,,doklejony” prostopadłościan o wymiarach $(1-2\varepsilon)\times(1-2\varepsilon) \times\varepsilon\sqrt{2}$. Łączna objętość tych prostopadłościanów jest zatem równa $6\cdot(1-2\varepsilon)^2\cdot\varepsilon\sqrt{2}$. Pomiędzy każdą parą sąsiednich prostopadłościanów znajduje się graniastosłup prosty o wysokości $(1-2\varepsilon)$ i podstawie będącej trójkątem prostokątnym, gdzie długość przyprostokątnej wynosi $\varepsilon\sqrt{2}$; sumaryczna objętość tych graniastosłupów to $12\cdot\frac{1}{2}\cdot(\varepsilon\sqrt{2})^2\cdot(1-2\varepsilon)$. Pozostały nam do wyliczenia objętości ośmiu ostrosłupów, które są umiejscowione pomiędzy sąsiednimi graniastosłupami. Ostrosłupy te mają tę samą podstawę co graniastosłupy, a ich wysokość równa jest $\varepsilon\sqrt{2}$. Ich objętość to $8\cdot\frac{1}{3}\cdot\frac{1}{2}\cdot(\varepsilon\sqrt{2})^3$. Objętość kostki Milki bez naroży jest więc równa
\[(1-2\varepsilon)^3+6\cdot(1-2\varepsilon)^2\cdot\varepsilon\sqrt{2}+12\cdot\frac{1}{2}\cdot(\varepsilon\sqrt{2})^2\cdot(1-2\varepsilon)+8\cdot\frac{1}{3}\cdot\frac{1}{2}\cdot(\varepsilon\sqrt{2})^3.\]
Objętość naroży wynosi natomiast
\[8\cdot\frac{1}{3}\cdot\frac{1}{2}\cdot(\varepsilon\sqrt{2})^3=\frac{\varepsilon^3\cdot8\sqrt{2}}{3},\]
czyli tyle samo ile wyliczyliśmy dla ostrosłupów.
Objętość kostki Milki wyraża się zatem następującym wzorem:
\[\operatorname{vol}(\varepsilon)=(1-2\varepsilon)^3+6\cdot(1-2\varepsilon)^2\cdot\varepsilon\sqrt{2}+12\cdot\varepsilon^2\cdot(1-2\varepsilon)+\frac{\varepsilon^3\cdot16\sqrt{2}}{3},\]
a gdy uporządkujemy wyrażenia algebraiczne, wzorem:
\[\operatorname{vol}(\varepsilon)=\Big(\frac{88\sqrt{2}}{3}-32\Big)\varepsilon^3+(24-24\sqrt{2})\varepsilon^2+(6\sqrt{2}-6)\varepsilon+1.\]
Po momencie analizy dojdziemy do wniosku, że dla odpowiednio małego $\varepsilon$ otrzymamy powierzchnię niewypukłej bryły o objętości większej niż $1$. Mamy bowiem:
\[\operatorname{vol}'(\varepsilon)=(88\sqrt{2}-96)\varepsilon^2+(48-48\sqrt{2})\varepsilon+6\sqrt{2}-6.\]
Pierwiastkami powyższego wielomianu są w przybliżeniu $0{,}1630$ oraz $0{,}5358$. Największą objętość osiągniemy zatem dla $\varepsilon$ równego około $0{,}1630$ – uzyskujemy objętość większą od wyjściowej o $18{,}20\%$ ($\operatorname{vol}(0{,}1630)\approx 1{,}1820$)! Co ciekawe, aby uzyskać objętość większą od $1,$ nie musimy wcale rozważać naroży, możemy je zwyczajnie uciąć. Największą objętość otrzymamy wtedy dla $\varepsilon=0{,}1425$, a procentowe zwiększenie objętości wyniesie ok. $16{,}88\%$. Zauważmy, że w pierwszym przypadku (z narożami) wykorzystujemy tyle samo materiału (kartonu czy też metalu), natomiast w drugim przypadku (bez naroży) – mniej materiału. Jesteśmy w stanie dokonać ulepszenia produkcji naszych pudełek na kakao – zużyjemy mniej kartonu, jednocześnie zwiększając ich pojemność5.
Ciosy karate
Nieco bardziej brutalny sposób na zwiększenie objętości przez deformację powierzchni zaproponował matematyk z Uniwersytetu Hawajskiego – David Bleecker. Zasugerował on, aby krawędziom wielościanu zadać ciosy karate. Efekt tego rozwiązania zastosowanego na czworościanie foremnym możemy podziwiać na rysunku poniżej. Zaskakujące jest to, że objętość w ten sposób zwiększy się aż o ok. $38\%$! Pomyślcie, o ile więcej kakao można byłoby zmieścić w takim opakowaniu przy takim samym zużyciu materiału!
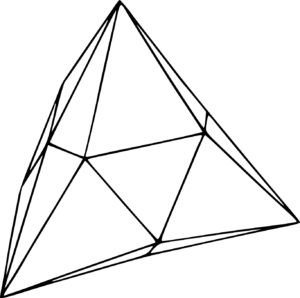
Deformacja Bleeckera na przykładzie czworościanu foremnego, którego objętość zwiększa się o około 38%. Rysunek pochodzi z artykułu Davida Bleeckera «Volume increasing isometric deformations of convex polyhedra» (Journal of Differential Geometry, 43, 1996)
Jak bardzo możemy zwiększyć objętość?
W 2006 roku wspomniany już Igor Pak udowodnił, że każda powierzchnia wielościenna (bez dziur) może być tak izometrycznie zdeformowana, że w wyniku tej deformacji zwiększy swą objętość. Każdy łasuch o matematycznym zacięciu bardzo się z tego cieszy – jest w stanie zdeformować wielościenne opakowanie tak, aby zmieścić w nim więcej ulubionego przysmaku.
Z drugiej strony nie możemy przecież zwiększać objętości w nieskończoność, bo powierzchnia w końcu się nam rozerwie. Wynik Igora Paka trzeba odczytywać zatem w ten sposób, że owszem, każda powierzchnia wielościenna może być tak zdeformowana, że zwiększy swoją objętość, ale przy bardziej skomplikowanych wielościanach to zwiększenie objętości może być ledwo zauważalne albo w ogóle niedostrzegalne – będzie nieskończenie małe. Warto się zatem zastanowić, czy jesteśmy w stanie jakoś oszacować maksymalną objętość, którą może ograniczać powierzchnia wielościenna. I tu z pomocą przychodzi nam tzw. nierówność izoperymetryczna. Jest ona uniwersalna, ponieważ można ją zapisać w ogólnej postaci dla przestrzeni dowolnego wymiaru. Nas będzie interesować wersja tej nierówności dla realizacji dwuwymiarowej powierzchni $S$ w trzecim wymiarze. Wygląda ona następująco:
\[{\text{vol}}(S)\leqslant \frac{1}{6\sqrt{\pi}}(\text{a}(S))^\frac{3}{2},\]
gdzie ${\text{vol}}(S)$ oznacza objętość wielościanu ograniczonego powierzchnią $S$, natomiast ${\text{a}}(S)$ – pole powierzchni $S$. Widzimy, że objętość jest odgórnie ograniczona przez stałą zależną od powierzchni naszego wyjściowego wielościanu.
| Wielościan | Ograniczenie |
|---|---|
| czworościan foremny | $0{,}2143$ |
| sześcian | $1{,}3820$ |
| ośmiościan foremny | $0{,}6063$ |
| dwunastościan foremny | $8{,}8210$ |
| dwudziestościan foremny | $2{,}3965$ |
Jak bardzo możemy zatem zwiększyć objętość? Niestety, nie wiemy tego dokładnie – powyższa zależność daje nam tylko pewne oszacowanie, a nie precyzyjną odpowiedź. Spójrzmy jednak na następujące przykłady. Będą one dość niestandardowe. Od teraz przyjmujemy konwencję, że wielościanem wypukłym jest też podwójnie pokryty wielokąt – tzn. taki wielokąt, który został zszyty brzegiem ze swoją wierną kopią w taki sposób, że leżą dokładnie na sobie. Przykładem może być opakowanie czipsów – tu mamy do czynienia z podwójnie pokrytym prostokątem. Odłóżmy na bok znane nam deformacje, w wyniku których z powierzchni wielościennej dostajemy znowu powierzchnię wielościenną. Tym razem rozważmy nadmuchiwanie wielościanów. Empirycznie każdy z nas jest w stanie stwierdzić, że po nadmuchaniu wielościanu nie otrzymamy już powierzchni wielościennej, tylko coś gładkiego lub miejscami gładkiego. Powiemy, że powierzchnia jest nienadmuchiwalna, kiedy nie jesteśmy już w stanie zwiększyć jej objętości. I tu mała uwaga – dlaczego Igor Pak udowodnił, że każda powierzchnia wielościenna może być tak zdeformowana, że zwiększy swoją objętość, a teraz nagle mówimy, że istnieją powierzchnie nienadmuchiwalne, czyli takie, które swojej objętości zwiększyć nie mogą? Odpowiedź już po cichu padła – nadmuchiwanie to deformacja, w wyniku której otrzymujemy obiekty niewielościenne, natomiast twierdzenie Paka dotyczy wyłącznie deformacji izometrycznych zachowujących ,,wielościenność”. Jeśli chodzi o nierówność izoperymetryczną, to odnosi się ona do jakiejkolwiek zamkniętej powierzchni – zarówno takiej wielościennej, jak i gładkiej, wypukłej czy wklęsłej.
Weźmy teraz na warsztat podwójnie pokryty kwadrat i spróbujmy go maksymalnie nadmuchać, aby otrzymać ,,idealną poduszkę”, czy też – jak to wcześniej nazwaliśmy – powierzchnię nienadmuchiwalną. Problem obliczenia objętości ograniczonej przez idealną poduszkę znany jest pod nazwą tea bag problem lub paper bag problem6.

Poduszka w rzeczywistości i teoretyczny kształt idealny. Grafika pochodzi z artykułu Igora Pak’a «Inflating polyhedral surfaces», 2006
W artykułach matematycznych można znaleźć deformacje, które dla podwójnie pokrytego kwadratu dają zwiększenie objętości o ok. $21\%$. Dla porównania nierówność izoperymetryczna daje nam ograniczenie górne na zwiększenie objętości w wysokości ponad $26\%$ (spróbujcie policzyć to sami dla podwójnie pokrytego kwadratu o boku jeden). Mamy więc pięcioprocentową ,,lukę” – i nie wiemy, czy istnieje taka deformacja, która tę lukę mogłaby zmniejszyć.
Balon Mylar
Bardziej dociekliwi czytelnicy zapytają – dlaczego rozważamy tylko deformacje obiektów wielościennych, a nie na przykład rzeczy bardziej krągłych? Odpowiedź nie jest wyszukana – objętości rzeczy wielościennych jest łatwiej wyliczyć, jednak nic nie stoi na przeszkodzie, aby zająć się podwójnie pokrytym kołem i jego nadmuchiwaniem. Nienadmuchiwalna forma, która z niego powstaje, znana jest pod angielską nazwą mylar balloon i można ją zobaczyć na rysunku poniżej. Mylar to nazwa nierozciągliwego materiału, z którego ten balon jest zrobiony. Zabraniamy przecież naszym deformacjom, aby rozciągały bądź rozdzierały powierzchnie.

Balon mylar. Grafika pochodzi z artykułu Igora Paka «Inflating polyhedral surfaces» (2006)
| $n$ | ograniczenie |
|---|---|
| 3 | $0{,}3938$ |
| 4 | $0{,}7523$ |
| 5 | $0{,}9751$ |
| 6 | $1{,}1138$ |
| 7 | $1{,}2039$ |
| 8 | $1{,}2651$ |
| 9 | $1{,}3084$ |
| 10 | $1{,}3400$ |
| 11 | $1{,}3637$ |
| 12 | $1{,}3820$ |
| 13 | $1{,}3963$ |
Zwróćmy uwagę na ,,zmarszczki” powstające na powierzchni fizycznego modelu. Zjawisko to zostało po raz pierwszy zauważone przez Williama Paulsena (ang. crimping of non-inflatable surfaces). Co ciekawe, dystrybucja fałd jest największa na równiku, natomiast na biegunach sfałdowań nie ma. Stawia się tezę, że objętość maksymalizuje się w momencie osiągnięcia powierzchni obrotowej oraz że powstają wtedy zmarszczki.
Mimo że balon mylar nie jest wielościenny, to może znaleźć on zastosowanie do badania powierzchni wielościennych. Przypuszcza się, że może on dać lepsze oszacowanie górne dla maksymalnej objętości podwójnie pokrytego $n$-kąta niż nierówność izoperymetryczna. ,,Przypuszcza się”, ponieważ żeby to stwierdzić z pewnością, musielibyśmy wiedzieć, że nadmuchując do oporu daną powierzchnię, otrzymamy powierzchnię nienadmuchiwalną o unikatowym kształcie – a to jest otwarty problem czekający na satysfakcjonujące rozwiązanie. Nawet najlepiej zaprojektowane fizyczne eksperymenty nie zastąpią matematycznego dowodu.
Gdybyśmy jednak na chwilę założyli słuszność tej hipotezy, mamy następującą sytuację – dla podwójnie pokrytego koła jedyną formą nienadmuchiwalną jest balon mylar. Gdy jest on nadmuchany z podwójnego koła jednostkowego, osiąga objętość w przybliżeniu 1,2185 jednostek sześciennych. Oznaczmy przez $W_{n}$ wielokąt foremny wpisany w okrąg jednostkowy, a poprzez $S_{n}$ podwójnie pokryty $W_{n}$, który – jak już wiemy – traktujemy jako wypukłą powierzchnię w $\mathbb{R}^3$. Skoro $W_{n}$ jest wpisany w okrąg jednostkowy, analogicznie możemy powiedzieć, że $S_{n}$ jest wpisany w podwójnie pokryte koło jednostkowe. Intuicja sugeruje nam, że po nadmuchaniu dowolnego $S_{n}$ jego objętość będzie mniejsza niż objętość balonu mylar. Istotnie, okazuje się, że dla odpowiednio dużego $n$ balon mylar lepiej ogranicza nam od góry maksymalną objętość niż nierówność izoperymetryczna! Spójrzmy bowiem na tabelę powyżej i porównajmy jej wartości z $1{,}2185$. Weźmy przykładowo $n=6$, dla którego nierówność izoperymetryczna daje nam ograniczenie $1{,}1138$ – jest to niewątpliwie dokładniejsze oszacowanie niż ,,mylarowe”. Jednakże już dla $n=8$ nierówność izoperymetryczna nie jest już tak satysfakcjonująca – daje nam oszacowanie $1{,}2651$, czyli więcej niż objętość balonu. Widzimy zatem, że badanie powierzchni niewielościennych może nam pomóc w zrozumieniu natury powierzchni wielościennych i na odwrót.
Bibliografia
- Jerzy Bednarczuk, Marek Kordos, Witold Sadowski, Ruchome wielościany, Matematyka-Społeczeństwo-Nauczanie, 35 (2005), s. 20-24
- David Bleecker, Volume increasing isometric deformations of convex polyhedra, J. Differential Geometry, 43 (1996), s. 505-526
- Robert Connelly, The Rigidity of Polyhedral Surfaces, Mathematics Magazine, 52 (1979), s. 275-283
- Peter R. Cromwell, Polyhedra, Cambridge University Press, Cambridge 1997
- Robert Connelly, Idzhad Sabitov, Anke Walz, The Bellows Conjecture, Contributions to Algebra and Geometry, 38 (1997), s. 1-10
- Herman Gluck, Almost all simply connected closed surfaces are rigid, Geometric Topology, Lecture Notes in Mathematics 438, Springer, Berlin 1975, s. 225-239
- Igor Pak, Inflating the cube without stretching, arXiv:math/0607754v1, 2006
- Igor Pak, Inflating polyhedral surfaces, 2006, http://www.math.ucla.edu/~pak/papers/pillow4.pdf
- Ian Stewart, The Bellows Conjecture, Scientific American, July 1998
- Ian Stewart, Histerie matematyczne, Prószyński i S-ka, Warszawa 2007
Przypisy
- Będziemy rozważać tu ,,idealistyczne” opakowania, tj. klejone wzdłuż krawędzi siatki (bez żadnych zakładek).
- Czy powierzchni wielościennej – pojęć tych będziemy używać wymiennie, choć intuicyjnie wyczuwamy, że nie są to tożsame pojęcia.
- Cięcia są zabronione, ponieważ nie zachowują ciągłości.
- Na płaszczyźnie wymagamy zachowania odległości ,,po krawędziach” pomiędzy dowolnymi dwoma punktami należącymi do krawędzi.
- Dlaczego więc wytwórcy opakowań nie dążą do takiej optymalizacji produkcji, a opakowania prostopadłościenne są najbardziej popularne? Nie jest to bardzo zaskakujące – produkcja masowa nie lubi skomplikowanych rozwiązań.
- W przypadku nadmuchiwania opakowań od czipsów problem ten mógłby zostać nazwany cheated bag problem. Wątpliwe jest bowiem to, że producenci czipsów dołożą więcej produktu do paczki – raczej wpompują tam więcej powietrza…
Artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.
