Wstęp
W salonie fryzjerskim siedzi matematyk, obok połyskująca para nożyczek, mnóstwo szczotek i innych sprzętów. Nerwowo wierci się w fotelu – przecież nie od dziś wie, że sfery zaczesać się nie da. Fryzjer intuicyjnie sięga po nożyczki, szalejące nad czołem rozmaitości nie rokują zbyt dobrze. Niechętny rozspójnieniu klient wpada na pomysł – warkocz będzie idealny!
U progu XX wieku Emil Artin wprowadził do topologii kolejną dziedzinę (pozornie) blisko związaną z codziennością. Teoria warkoczy znajduje szerokie zastosowania między innymi w biologii i kryptografii, a także w teorii węzłów. Niniejszy artykuł stanowi elementarne zaproszenie do rozważań tego zagadnienia przedstawiając niezbędne definicje i fakty odnośnie struktury grup warkoczy oraz klasyczne algorytmy czesania.
Zachęcam do aktywnego czytania – większość przekształceń można zbadać empirycznie, wystarczą cztery kawałki sznurka.
Czym jest warkocz dla matematyka?
Dla normalnego1 człowieka warkocz stanowią zaplecione pasma włosów, sznurków etc. Dla wygody (i z empirycznego doświadczenia) wprowadzamy pewne uproszczenia, mianowicie zakładamy, że rozważać będziemy $n$-pasmowe warkocze umieszczone wewnątrz walca, wszystkie pasma mają równą długość, a końce zaczepione są w różnych punktach podstaw. Zakładamy, że wszelkie przeplecenia odbywają się wewnątrz „tuby”, w żadnym punkcie dwa pasma nie łączą się w jedno (nie przecinają się) i nie mogą zawracać. Nie ma też obawy, że ustalona długość pasm i skomplikowanie przepleceń spowoduje, że któreś nie dotrze do punktu zaczepienia końców – topologia to w uproszczeniu „giętka geometria” – nie ma problemu z ich rozciąganiem2
Tak więc wybieramy po $n$ punktów na podstawach walca (ułożonego w poziomie), powiedzmy $p_{1}, p_{2}, \ldots, p_{n}$ na lewej podstawie oraz $q_1, q_2, \ldots, q_n$ na prawej podstawie. Rozpoczynając od punktów $p_i$ odbywa się splot aż do punktów zaczepienia $q_j$. Fachowo warkoczem geometrycznym $\beta$ nazywamy układ (ciąg) $(b_1, b_2,\ldots, b_n)$ giętkich pasm3, które zaplatają się wewnątrz walca tak jak na rysunku poniżej.

Przykładowy warkocz geometryczny
Warto zwrócić uwagę na zachowanie pasm na podstawach walca. Przypuśćmy, ze pasmo $b_1$ zaczynające się w punkcie $p_1$ (będziemy wtedy pisać $b_1(0)=p_1$ dla skrócenia zapisu) na lewej podstawie, kończy się w punkcie $q_2$ (inaczej: $b_1(1)=q_2$) na prawej podstawie. Podobnie pasmo $b_2$ zaczyna się w punkcie $p_2$ ($b_2(0)=p_2$) i kończy się w punkcie $q_5$ (czyli $b_2(1)=q_5$) itd. Wówczas połączenia między podstawami możemy zapisać jako
\[\begin{pmatrix}
p_1 & p_2& \dots & p_n\\
q_2& q_5& \dots & \dots
\end{pmatrix},\]
albo prościej (pozostawiając tylko indeksy)
\[\begin{pmatrix}
1 & 2& \dots & n\\
2 & 5& \dots & \dots
\end{pmatrix}.\]
Tak więc widzimy, że warkocz definiuje nam przyporządkowanie liczbom ze zbioru $\lbrace 1,2,\ldots,n\rbrace$ liczb z tego samego zbioru (niekoniecznie innych)4. Z powodu ograniczeń dla pasm każdy punkt $p_i$ po lewej znajdzie dokładnie jeden punkt zaczepienia $q_j$ po prawej. Pasmo $b_i$, które zaczyna się w punkcie $p_i$ a kończy się w $q_j$ oznacza, że w zapisie powyżej pod liczbą $i$ w górnym wierszu znajduje się liczba $j$ w dolnym. Z kolei pod liczbą $j$ w górnym wierszu będzie stała jeszcze inna itd.
Takie przyporządkowanie (różnowartościowe), opisujące takie przestawienia lub przetasowania liczb nazywa się fachowo: permutacjami. Permutacja pochodząca od warkocza $\beta = (b_1,\ldots, b_n)$ nazywamy permutacją indukowaną przez ten warkocz.
Dwakroć zapleciony „taki sam” warkocz (mimo usilnych chęci czeszącego) zawsze wygląda odrobinę inaczej. Jednak fakt, że możemy użyć określenia „taki sam” pozwala nam wnioskować, że niektóre warkocze reprezentują ten sam „typ”, „rodzaj” warkocza (chociażby kłos, francuz, czy klasyczny trójpasmowy). Zatem dwa warkocze uznamy za równoważne, jeśli jeden powstaje z drugiego poprzez powyginanie pasm z zaczepionymi nieruchomo końcami. Permutacja indukowana jest zatem ustalona dla konkretnej klasy warkoczy.
Struktura grupy
Grupa to jedno z fundamentalnych pojęć w matematyce. Prześledzimy je na przykładzie zbioru liczb rzeczywistych bez zera $\mathbb{R}\setminus \lbrace 0 \rbrace$. Zbiór wraz z działaniem (u nas mnożeniem) nazywamy grupą, gdy wskazane działanie jest łączne (to znaczy $a(bc)=(ab)c$ ) oraz istnieją w nim szczególne elementy – element neutralny ($1$) i dla każdego elementu można wskazać element odwrotny (dla liczby $a$ odwrotnością jest $\frac{1}{a}$).
Z warkoczami, poprzez permutacje indukowane, nieodłącznie związana jest grupa permutacji. Grupą permutacji $S_n$ nazywamy zbiór permutacji na $n$ elementach wraz z działaniem składania, któremu przyjrzymy się na przykładzie grupy $S_3$.
\begin{align*}
S_3 &=\bigg\lbrace \begin{pmatrix}
1 & 2& 3\\
1& 2&3
\end{pmatrix}, \begin{pmatrix}
1 & 2& 3\\
1& 3&2
\end{pmatrix}, \begin{pmatrix}
1 & 2& 3\\
2& 1 &3
\end{pmatrix},\\
&\qquad \begin{pmatrix}
1 & 2& 3\\
2&3 &1
\end{pmatrix}, \begin{pmatrix}
1 & 2& 3\\
3&1&2
\end{pmatrix}, \begin{pmatrix}
1 & 2& 3\\
3& 2& 1
\end{pmatrix}\bigg\rbrace .\end{align*}
Rolę elementu neutralnego pełni: $\begin{pmatrix}
1 & 2& 3\\
1& 2&3
\end{pmatrix}$. Pozostaje się jeszcze zastanowić, jak uzyskać wynik złożenia:
\[ \begin{pmatrix}
1 & 2& 3\\
3& 2& 1
\end{pmatrix} \cdot \begin{pmatrix}
1 & 2& 3\\
2&3 &1
\end{pmatrix}=\begin{pmatrix}
1 & 2& 3\\
2&1&3
\end{pmatrix}?\]
Zaczynamy od wewnętrznej permutacji, która przesyła $1\mapsto2$, z kolei zewnętrzna $2\mapsto2$, więc łącząc te dwa warunki dostajemy w wyniku $1\mapsto2$. Podobnie postępując z $2$ i $3$ uzyskujemy permutację końcową. Zamieniając permutacje miejscami otrzymujemy inny wynik:
\[ \begin{pmatrix}
1 & 2& 3\\
2&3 &1
\end{pmatrix} \cdot \begin{pmatrix}
1 & 2& 3\\
3& 2& 1
\end{pmatrix} =\begin{pmatrix}
1 & 2& 3\\
1&3&2
\end{pmatrix}.\]
Dla każdego elementu z $S_3$ znajdziemy też element do niego przeciwny – polecam samodzielne poszukiwania jako ćwiczenie.
Podobnie w zbiorze warkoczy na określonej liczbie pasm wprowadzamy działanie składania warkoczy. Intuicyjnie można je rozumieć jako przedłużenie jednego warkocza drugim poprzez związanie pasm. Wyobraźmy sobie dwa identyczne walce z warkoczami wewnątrz o ustalonej liczbie pasm. Przyjmijmy, że końce pierwszego warkocza i punkty zaczepienia drugiego występują dokładnie w tych samych miejscach na podstawach5. Zestawiamy te walce tak, aby wskazane punkty się spotkały i sklejamy pasma na styku. Mamy więc walec o podwójnej wysokości6 ze związanymi dwoma warkoczami. Jeżeli go przeskalujemy do jednostkowego to znów mamy twór spełniający definicję warkocza geometrycznego a tym samym wynik działania7, co widać na poniższym rysunku.
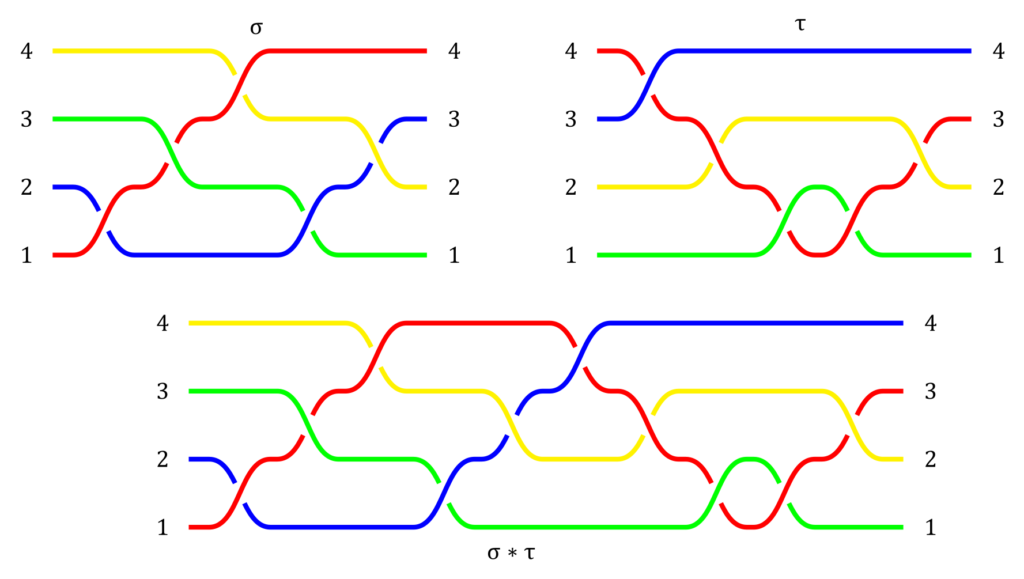
Złożenie warkoczy $\sigma$ i $\tau$ (górny rząd) otrzymamy przez sklejenie ich końców. Złożenie permutacji indukowanych przez $\sigma$ i $\tau$ daje permutację indukowaną przez $\sigma \ast \tau$.
Nietrudno zauważyć, że takie określenie spełnia aksjomaty grupy: zachodzi łączność, mamy warkocz trywialny o prostych pasmach i dla każdego warkocza możemy wskazać warkocz do niego odwrotny — odbicie lustrzane.
Twierdzenie. Zbiór warkoczy na $n$-pasmach wraz z działaniem składania tworzy grupę oznaczoną symbolem $B_n$. Grupa $B_n$ nie jest przemienna.
Zauważmy również, że permutacją indukowaną przez złożenie warkoczy jest złożenie odpowiednich permutacji8. Przykładowo, na rysunku powyżej pierwszy z warkoczy indukuje permutację
\[
\begin{pmatrix}
1 & 2& 3&4\\
4&3 &1&2
\end{pmatrix}
\]
zaś drugi
\[
\begin{pmatrix}
1 & 2& 3&4\\
1&2 &4&3
\end{pmatrix}.
\]
Ich złożenie to
\[\begin{pmatrix}
1 & 2& 3&4\\
4&3 &1&2
\end{pmatrix} \cdot \begin{pmatrix}
1 & 2& 3&4\\
1&2 &4&3
\end{pmatrix} =\begin{pmatrix}
1 & 2& 3&4\\
3&4 &1&2
\end{pmatrix},\]
czyli permutacja wyniku.
Warto również zwrócić uwagę na to, że złożenie powyższych permutacji w odwrotnej kolejności da inny wynik. To pokazuje, że złożenie warkoczy $\tau \sigma$ nie będzie tym samym co $\sigma \tau$.
Zapiszmy to słowami!
Aby usystematyzować opis warkoczy9 wprowadza się tak zwane warkocze elementarne, czyli „cegiełki” budulcowe każdego warkocza. Precyzyjniej, warkoczem elementarnym $\sigma_i$ nazywamy warkocz, w którym występuje tylko jedno przeplecenie: $(i+1)$-sze pasmo przecina $i$-te ponad nim, a pozostałe pasma pozostają proste. Jego odwrotnością $\sigma_i^{-1}$ jest warkocz elementarny, w którym $i$-te pasmo przechodzi ponad $(i+1)$-szym.

Warkocz elementarny $\sigma_i$ ($(i+1)$-sze pasmo – zielone przechodzi ponad $i$-tym – niebieskim) oraz warkocz do niego odwrotny $\sigma_{i}^{-1}$.
Odpowiednio „rozluźniając” sploty możemy podzielić dowolny warkocz na segmenty, w których występuje tylko jedno przełożenie pasm odpowiadające konkretnemu warkoczowi elementarnemu:
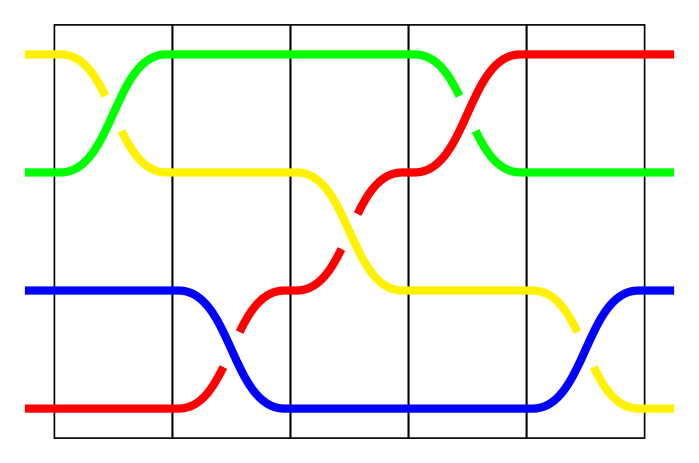
Przedstawienie warkocza za pomocą słów; na rysunku warkocz $\sigma_3^{-1}\sigma_1\sigma_2\sigma_3^{-1}\sigma_1^{-1}$.
Taki opis niestety nie jest jednoznaczny.
Zastanówmy się, czy warkocz z rysunku poniżej „bardzo” się zmieni, jeśli zamiast pierwszego przełożenia pasm żółtego i zielonego wykonać je najpierw na paśmie niebieskim i czerwonym? Biorąc pod uwagę giętkość i ciągliwość zmiana nie będzie istotna. Podobnie pod koniec skrzyżowania czarno-niebieskie i zielono-czerwone są od siebie niezależne i można je w „dozwolony” sposób zamienić.
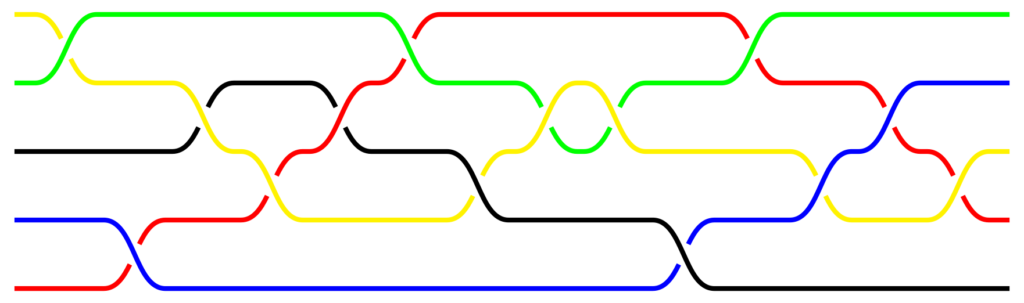
Zamiana kolejności pierwszych dwóch skrzyżowań (licząc od lewej) daje równoważny warkocz.
Jak zatem sprawdzić kiedy dwa warkocze są takie same, a inne słowa opisują ten sam warkocz? Problem ten rozstrzyga twierdzenie pochodzące od Artina i Magnusa. Wyróżnia ono trzy typy niejednoznaczności zapisu warkoczy:
- Złożenie warkoczy elementarnych $\sigma_i \sigma_i^{-1}$ oraz $\sigma_i \sigma_i^{-1}$ jest równoważne warkoczowi trywialnemu (o tym mówiliśmy już wcześniej).
- Jeśli w warkoczach elementarnych $\sigma_i$ oraz $\sigma_j$ przeplecenia występują na niezależnych pasmach (tzn. $\vert i – j \vert \ge 1$), wówczas warkocz $\sigma_i \sigma_j$ jest równoważny warkoczowi $\sigma_j \sigma_i$. Oto przykład:
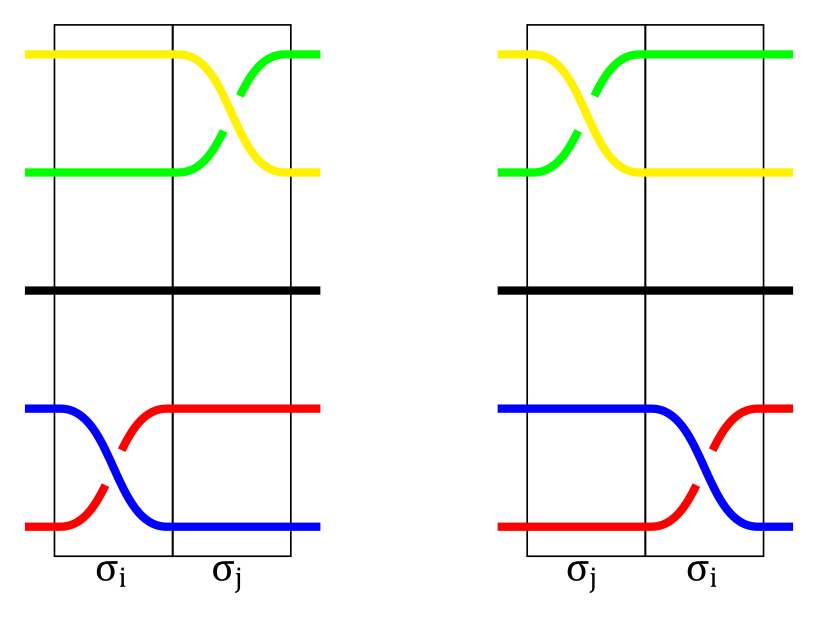
Przeploty pasm niezależnych – zamiana ($\sigma _{i}\sigma_{j} = \sigma_{j}\sigma_{i}$, gdzie $\vert i – j \vert \ge 1$).
- W przypadku gdy przeplecenia w warkoczach elementarnych $\sigma_i$ oraz $\sigma_j$ posiadają jedno wspólne pasmo (czyli $j = i \pm 1$), wówczas warkocz $\sigma_i \sigma_j \sigma_i$ jest równoważny $\sigma_j \sigma_i \sigma_j$, co widać poniżej.
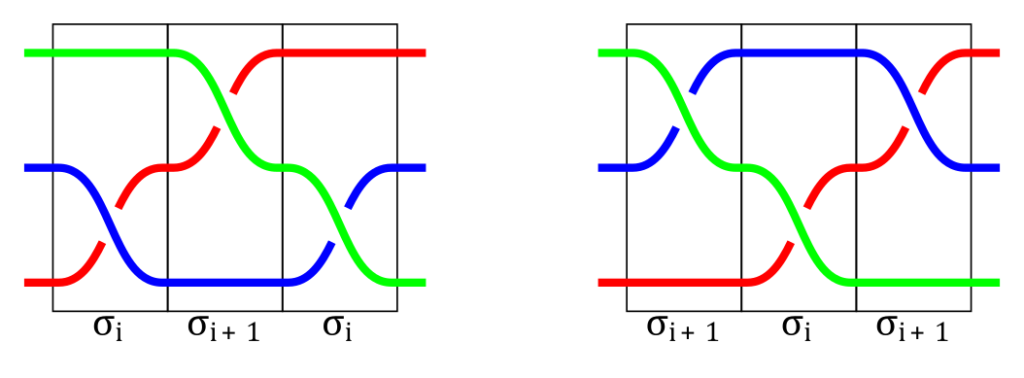
Przeploty sąsiednich pasm – zamiana ($\sigma _{i}\sigma_{i+1}\sigma_{i} = \sigma _{i+1}\sigma_{i}\sigma_{i+1}$, gdzie $ 1 \leqslant i \leqslant n-2$).
Co ciekawe taka reprezentacja, z pozoru wygodniejsza, nastręcza pewnych trudności. Mając dane dwa słowa teoretycznie możemy rozstrzygnąć, czy „kodują” ten sam warkocz. Niestety wspomniane twierdzenie nie daje algorytmicznej formuły na rozstrzygnięcie tego problemu. W praktyce stosuje się inne metody do porównywania warkoczy.
Problem słów – algorytmy
Czasem codzienność wymusza od nas syzyfową pracę rozplątywania różnych rzeczy, chociażby kabli. Zdarza się, że sprawiający pozory węzła gordyjskiego chaos ulega szybciej niż można by przypuszczać po wstępnym oglądzie (nie dotyczy to rzecz jasna słuchawek). W przypadku warkoczy orzeczenie, czy być może skomplikowana plątanina rzeczywiście coś splotła, czy nie, jest tym samym co warkocz trywialny (o prostych pasmach) jest zagadnieniem z kombinatorycznej teorii grup zwanym problemem słów.
W dalszej części przyjrzymy się metodom rozstrzygania go. Przedstawione algorytmy są dalekie od optymalnych dla komputera i w praktyce raczej ustępują miejsca innym.
Potrzebne będą warkocze czyste, czyli takie, które indukują trywialną permutację (taką, która nie zmienia układu końców). Innych nie ma sensu rozpatrywać, ponieważ nie mogą być równoważne z trywialnym. To wynika z faktu, że dozwolone manipulacje przepleceniami (rozluźnianie i przesuwanie) nie mają wpływu na końce warkocza.
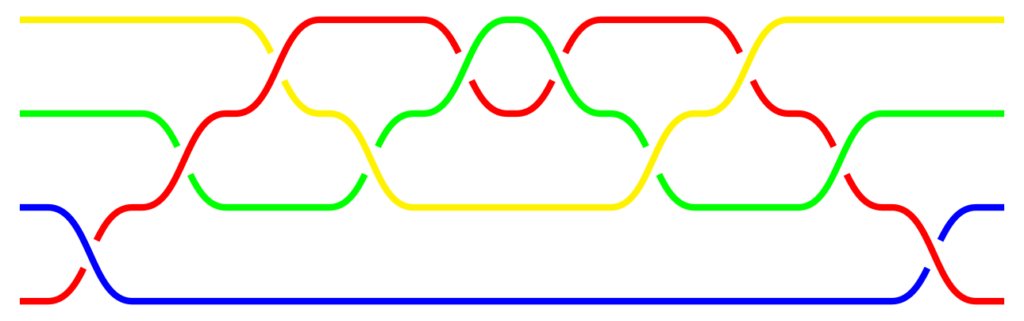
Warkocz czysty. Początki i końce pasm znajdują się na tej samej wysokości.
Jak rozczesać bałagan na głowie? Grzebień Artina
W 1926 roku ukazał się artykuł autorstwa Emila Artina „Theorie der Zöpfe”, w którym przedstawił on algorytm „czesania” (porządkowania kolejności przepleceń) warkoczy. Weźmy $n$-warkocz czysty $\beta$ i rozczeszmy go10:
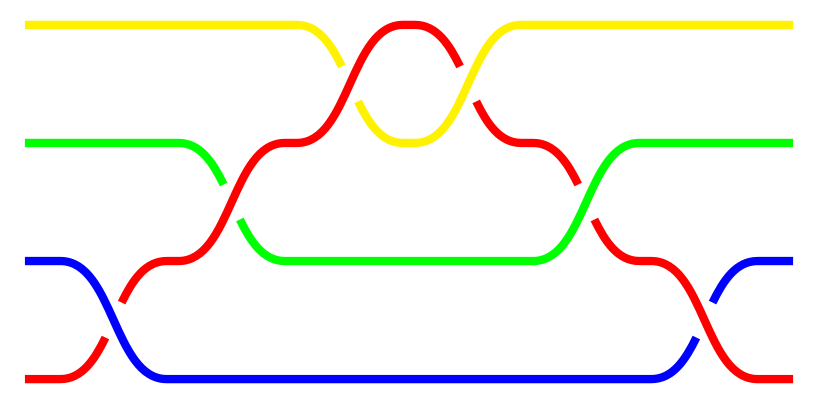
Warkocz $\beta$.
- [KROK 1] Tworzymy kopię warkocza $\beta$ i usuwamy z niej pierwsze pasmo od góry zastępując je prostym, otrzymany w ten sposób warkocz nazywamy $\gamma_1$.
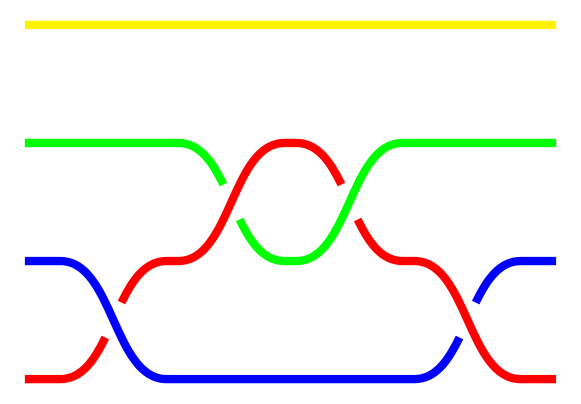
Warkocz $\gamma_1$.
- [KROK 2] Składamy $\beta \gamma_1^{-1}=\alpha_1$ i redukujemy zgodnie ze zbiorem relacji (te kroki pokazano na rysunkach poniżej). Nasz wyjściowy warkocz możemy zapisać jako $\beta =\alpha_1\gamma_1$, napinamy wszystkie pasma poza pierwszym. Wówczas w tej części warkocza w każdym przepleceniu bierze udział żółte pasmo i nie bierze udziału w dalszej części splotu.
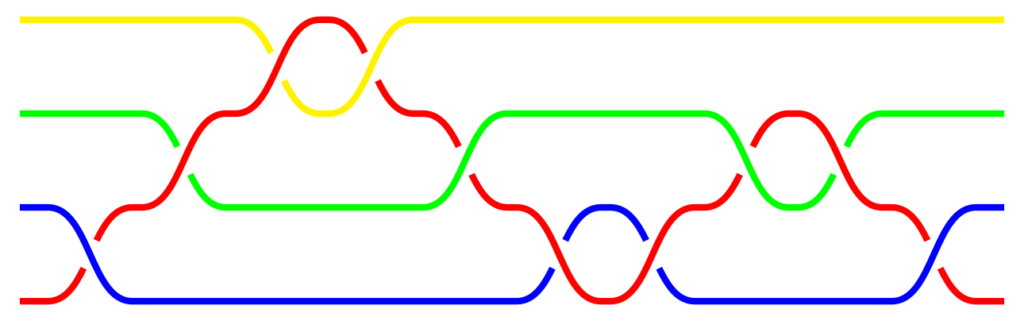
Warkocz $\alpha_1=\beta\gamma_1^{-1}$.
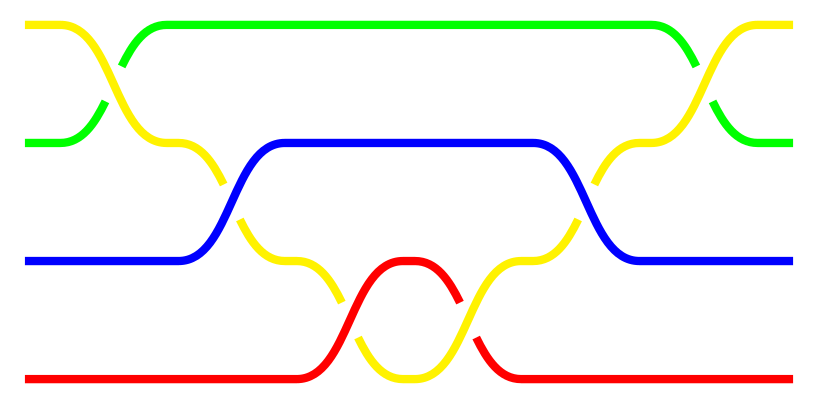
Warkocz $\alpha_1$ po naciągnięciu pasm.
- [KROK 3] Procedurę opisaną w krokach 1 i 2 powtarzamy dla warkocza $\gamma_1$.
- [KROK 4] Po odpowiedniej liczbie powtórzeń otrzymujemy rozkład $\beta=\alpha_1\ldots\alpha_{n-1}$, w którym każdy z segmentów $\alpha_i$ jest „wyczesany”.

Postać normalna warkocza $\beta$
Tak uzyskany „wyczesany” rozkład nazywamy postacią normalną. Dla każdego warkocza istnieje dokładnie jeden „wyczesany” warkocz, w którym wszystkie $\alpha_i$ są zredukowane zgodnie z relacjami. Jak łatwo się domyślić badany warkocz jest równoważny trywialnemu wtedy i tylko wtedy, gdy po czesaniu jest trywialny (ma proste pasma).
Redukcja rączek
Przyjrzymy się teraz drugiej metodzie rozstrzygania problemu słów w grupie warkoczy zaproponowanej przez Patricka Dehornoy’a w 1997 roku. Redukcja rączek polega na wskazaniu podwarkoczy określonego typu – tzw. rączek11, które stopniowo opuszczane za pomocą pewnego odwzorowania (homomorfizmu) rozplatają warkocz, a tym samym pozwalają na sprawdzenie jego trywialności. Podobnie jak poprzednio, będziemy rozpatrywać warkocze czyste.
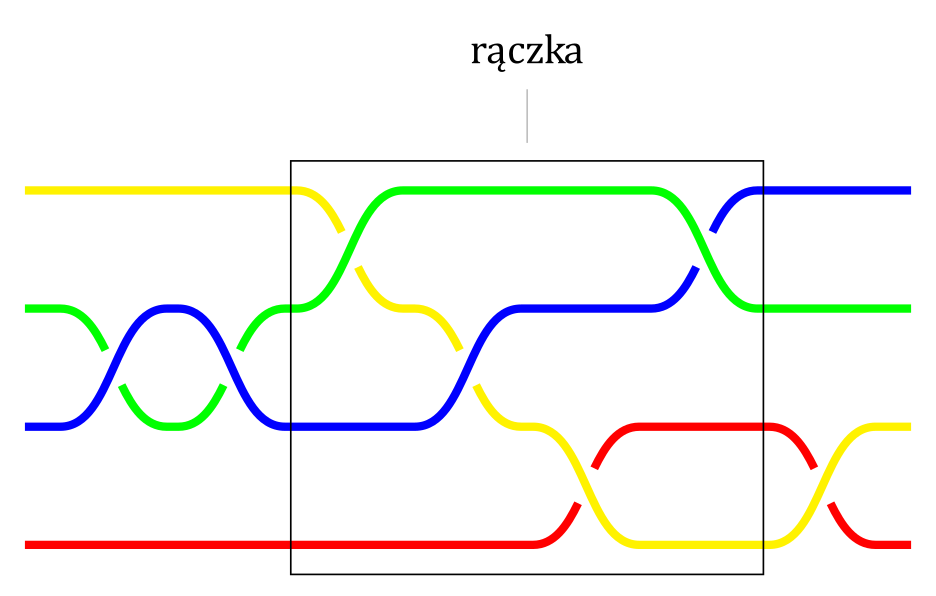
Warkocz zawierający rączkę.
Przesuwając się od początku warkocza po lewej znajdujemy pierwszą rączkę i opuszczamy ją. W otrzymanym warkoczu również szukamy rączki itd. aż do wyczerpania dostępnych rączek. W zależności od tego, czy końcowy warkocz jest trywialny, czy też nie dostajemy odpowiedź12
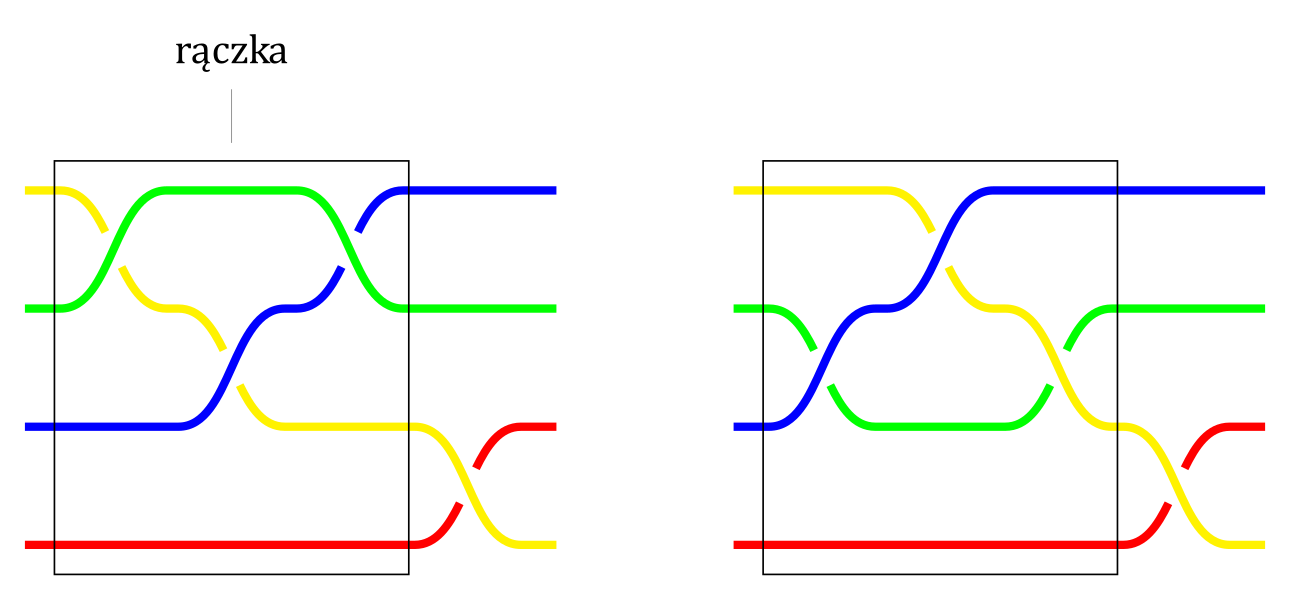
Rączka (na zielonym paśmie) przed (warkocz po lewej) i po redukcji (warkocz po prawej).
Nie ma obawy, że zmienimy warkocz w trakcie przeprowadzania redukcji, ponieważ korzystamy tylko z operacji dozwolonych (wskazanych przez twierdzenie Artina i Magnusa). Z algorytmicznego punktu widzenia sytuacja również jest dobra, ponieważ algorytm redukcji nigdy się nie zapętli.
Bibliografia
Na koniec uczesanych i zainteresowanych bliższym zgłębieniem tematu matematyków zachęcam do skorzystania z następujących prac:
- Emil Artin, Theory of braids, 1947.
- Ester Dalvit, New proposals for the popularization of braid theory, 2011.
- Krzysztof Pawałowski, Wielomiany Jonesa węzłów i splotów, 2012.
- Richard Smeltzer Linear Representations of Braid Groups, 2003.
- http://matematita.science.unitn.it/braids/index.html.
- http://www.math.unicaen.fr/tressapp/.
Przypisy
- Autorka nie próbuje tutaj definiować normalności, toż to sprawa konieczna dla rozważenia przez filozofów, jednak roboczo załóżmy, że przez normalność rozumieć będziemy człowieka nieskażonego wiedzą z zakresu wyższej matematyki. Wszak wszyscy doskonale wiedzą, że matematycy są wyjątkowymi okazami na tle społeczeństwa!
- Dla wygody pisania wzorów przyjmuje się jednostkową długość, którą zależnie od potrzeb można skalować.
- Formalnie rzecz biorąc, jest to układ funkcji, których wykresy są pasmami warkocza.
- A propos normalności – dla matematyka proste rozpuszczone pasma to też warkocz!
- Topologowi to obojętne, jak i wiele innych rzeczy, na plastycznym kole przesunięcie punktów to tylko trochę pracy (manualnej?)…
- Chyba nie muszę już powtarzać, że topolog to niewrażliwe na wiele spraw stworzenie?
- Aby opisać tę operację wzorami przyjmijmy, że $\beta$ i $\gamma$ są warkoczami geometrycznymi o $n$ pasmach z permutacjami $\sigma$ i $\tau$, odpowiednio.
Złożeniem (związaniem) $\beta$ i $\gamma$ nazywamy $n$-warkocz $\delta = \beta \ast \gamma $
\[\delta = (d_{1}, d_{2}, \ldots, d_{n}),\]
gdzie
\[d_{i}(t) = \left\lbrace
\begin{array}{cc}
b_{i}(2t) & t \in [0, \frac{1}{2}], \\
c_{\sigma(i)}(2t – 1) & t \in [\frac{1}{2}, 1]. \\
\end{array}\right. \]
Warto nadmienić, że jest to tradycyjne określenie mnożenia dróg zaczerpnięte z topologii algebraicznej. - Odwzorowanie grup $f\colon B_n \rightarrow S_n$, przypisujące każdemu warkoczowi jego permutację indukowaną, spełnia warunek $f(a\ast b)=f(a)\cdot f(b)$ dla $a,b\in B_n$. Odwzorowanie o tej własności nazywamy homomorfizmem.
- Może trafniej: Żeby za dużo nie pisać, w trakcie tłumaczenia co jak pleść (niekoniecznie trzy po trzy) i zaspokoić nieposkromioną żądzę znaczkologii…
- O ile wcześniej wyobraźnia starczała tu warto sięgnąć po sznurki.
- Formalnie, rączką nazywamy podwarkocz (podsłowo) postaci
\[
\sigma_i^ex\sigma_i^{-e}
\]
gdzie $e=\pm 1$, a $x$ złożony jest tylko z generatorów $\sigma_j^{\pm 1}$ przy $j\le i$. -
Dla dowolnego $1 \leqslant i \leqslant n$ określamy odwzorowanie $\phi_i : B_n\rightarrow B_n$ poprzez wprowadzenie zmian w słowie warkocza: warkocz elementarny $\sigma_i^{\pm 1}$ zastępujemy trywialnym, a warkocz $\sigma_{i-1}^{\pm 1}$ zamieniamy na fragment $\sigma_{i-1}^{-e}\sigma_i^{\pm1}\sigma_{i-1}^e$. Natomiast warkocze elementarne odpowiadające wskaźnikom $j\neq i-1, i$ pozostają niezmienione.
Artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.
