Najpierw masa…
Środek masy, albo barycentrum danego zbioru punktowych mas jest ich uśrednionym położeniem.
Zacznijmy skromnie − mamy układ dwóch punktów materialnych o jednakowej masie. Jest jasne, że środek masy tego układu jest środkiem odcinka łączącego te punkty.
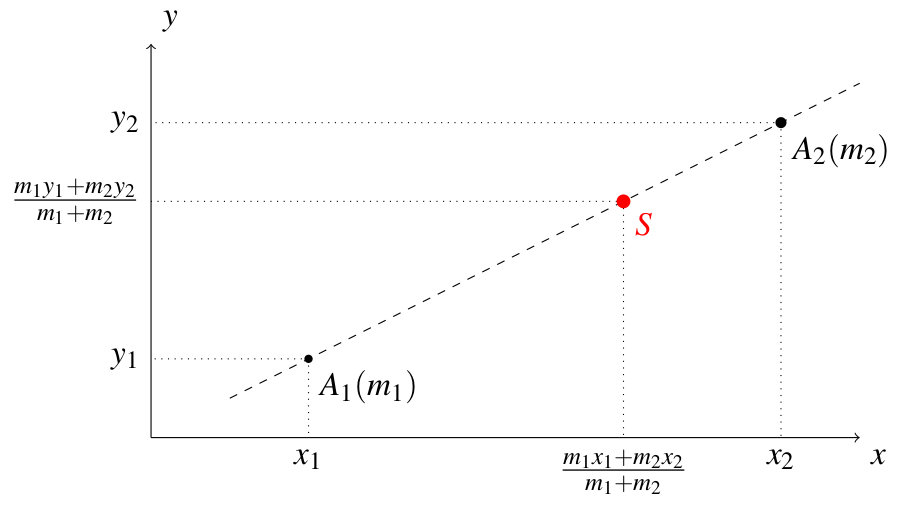
Nieco inaczej jest w przypadku, w którym dane dwa punkty mają różne masy. Niech będą to punkty \(A_1\) i \(A_2\) o dodatnich masach odpowiednio \(m_1\) i \(m_2\). Umieśćmy je na osi liczbowej, nadając im współrzędne odpowiednio \(x_1\) i \(x_2\). Literą \(S\) oznaczymy barycentrum tych dwóch punktów.
Załóżmy na początku, że \(m_1\) i \(m_2\) są liczbami naturalnymi. Punkt \(A_1\) możemy potraktować jako \(m_1\) mas jednostkowych położonych na współrzędnej \(x_1\), analogicznie z punktem \(A_2\). Zatem średnie położenie masy to
\[\frac{\overbrace{x_1+x_1+\ldots+x_1}^{m_1\text{ razy}} + \overbrace{x_2+x_2+\ldots+x_2}^{m_2\text{ razy}}}{m_1+m_2} = \frac{m_1x_1+m_2x_2}{m_1+m_2}.\]
Współrzędna punktu \(S\) jest więc średnią ważoną liczb \(x_1\) i \(x_2\), z wagami odpowiednio \(m_1\) i \(m_2\). Wzór ten stosujemy także gdy \(m_1\) i \(m_2\) nie są liczbami naturalnymi.
Możemy założyć, zgodnie z tym, co sugeruje rysunek, że \(x_1\lt x_2\). Wówczas \(x_1\lt \frac{m_1x_1+m_2x_2}{m_1+m_2}\lt x_2\), więc środek masy, czego należało się spodziewać, leży pomiędzy punktami \(A_1\) i \(A_2\). Prosty rachunek daje ponadto następujące zależności:
\begin{align*}
m_1\cdot|SA_1| & = m_1\cdot\left(\frac{m_1x_1+m_2x_2}{m_1+m_2}-x_1\right) = \frac{m_1m_2}{m_1+m_2}(x_2-x_1), \\
m_2\cdot|SA_2| & = m_2\cdot\left(x_2-\frac{m_1x_1+m_2x_2}{m_1+m_2}\right) = \frac{m_1m_2}{m_1+m_2}(x_2-x_1).
\end{align*}
Zatem \(m_1\cdot|SA_1|=m_2\cdot|SA_2|\), lub równoważnie\[\frac{m_1}{m_2}=\frac{|SA_2|}{|SA_1|}.\]
To oznacza, że w układzie dwóch punktów materialnych odległość barycentrum od każdego z nich jest odwrotnie proporcjonalna do jego masy. To zgodne z intuicją − im bardziej masywny punkt, tym bliżej niego położony jest środek masy.
Czytelnik być może zauważył, że równość \(m_1\cdot|SA_1|=m_2\cdot|SA_2|\) przypomina zasadę dźwigni dwustronnej. Jest to słuszne skojarzenie. Punkt \(S\) jest takim punktem podparcia kładki \(A_1A_2\), na której końcach znajdują się masy \(m_1\) i \(m_2\), dla którego znajduje się ona w stanie równowagi, przy czym masę samej kładki tu zaniedbujemy.
Zwiększymy teraz liczbę wymiarów: umieścimy punkty na płaszczyźnie. To samo możemy zrobić w przestrzeni, nawet \(n\)-wymiarowej, ale dla jasności rozważań poprzestaniemy na dwóch wymiarach. Wówczas barycentrum punktów \(A_1=(x_1,y_1)\) z masą \(m_1\) i \(A_2=(x_2,y_2)\) z masą \(m_2\) jest punkt
\[S = \left(\frac{m_1x_1+m_2x_2}{m_1+m_2},\; \frac{m_1y_1+m_2y_2}{m_1+m_2}\right).\]
Jego współrzędne wyznaczamy dokładnie tak samo jak w przypadku jednowymiarowym na osi liczbowej − wyznaczamy średnią współrzędną \(x\) oraz średnią współrzędną \(y\) masy całego układu.
Czytelnikowi biegłemu w geometrii analitycznej pozostawiamy sprawdzenie, że rzeczywiście punkt \(S\) leży na odcinku \(A_1A_2\) i spełnia warunek \(m_1\cdot|SA_1|=m_2\cdot|SA_2|\).
Powyższe definicje uogólniają się w naturalny sposób na większą liczbę punktów. Barycentrum układu punktów\[A_i=(x_i,y_i) \text{ z masą } m_i, \text{ dla } i=1,2,\ldots,n\]jest punkt
\[S=\left(\frac{m_1x_1+m_2x_2+\ldots+m_nx_n}{m_1+m_2+\ldots+m_n}, \frac{m_1y_1+m_2y_2+\ldots+m_ny_n}{m_1+m_2+\ldots+m_n}\right).\]
Jako przykład podajemy środek ciężkości trójkąta. Umieszczając w każdym wierzchołku trójkąta \(ABC\) jednakową masę \(m\), otrzymamy barycentrum w punkcie
\begin{align*}S & =\left(\frac{mx_A+mx_B+mx_C}{m+m+m},\frac{my_A+my_B+my_C}{m+m+m}\right)\\ & = \left(\frac{x_A+x_B+x_C}3,\frac{y_A+y_B+y_C}3\right),\end{align*}przy czym \(A=(x_A,y_A)\), \(B=(x_B,y_B)\) i \(C=(x_C,y_C)\). Jest to dobrze znany wzór na środek ciężkości trójkąta w układzie współrzędnych.
W niniejszym artykule rozważamy wyłącznie dodatnie masy, choć z matematycznego punktu widzenia nic nie stoi na przeszkodzie, by dopuścić masy ujemne, jednak trudniej je wtedy fizycznie zinterpretować. Drugą przyczyną takiego ograniczenia jest możliwość zerowania się mianownika \(m_1+m_2+\ldots+m_n\), a tego nie chcemy.
Dziel i rządź!
Zaczynamy teraz poważną matematykę! Poniższe twierdzenie daje nam alternatywną metodę wyznaczania barycentrum danego układu punktów.
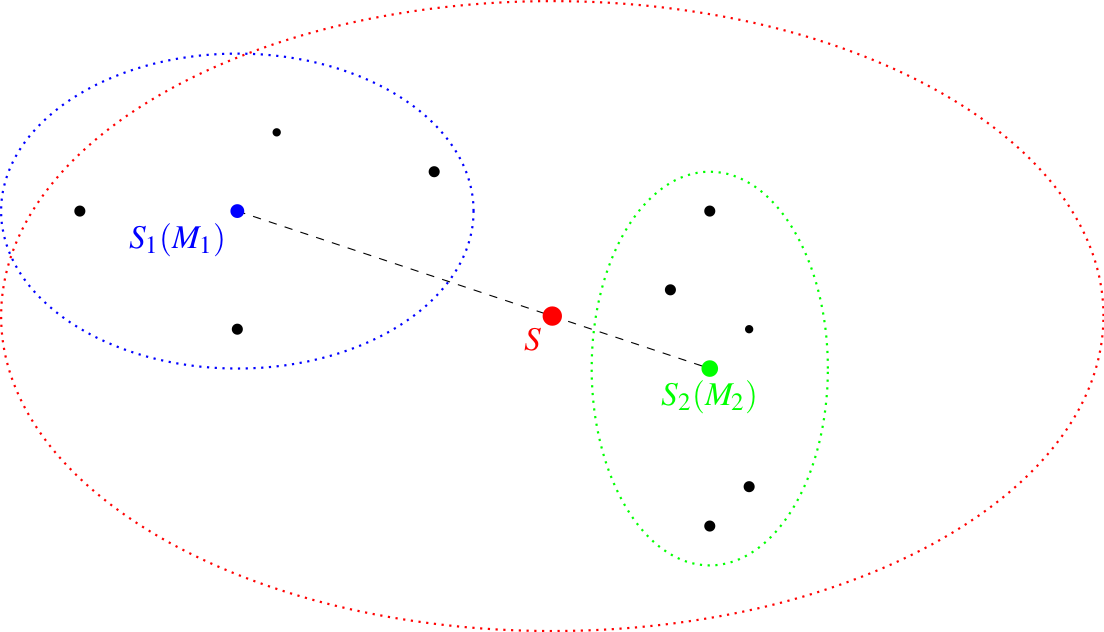
Twierdzenie 1. Podzielmy dany zbiór punktów z masami na dwa niepuste podzbiory. Niech jeden z nich ma łączną masę \(M_1\) i środek masy \(S_1\), a drugi łączną masę \(M_2\) i środek masy \(S_2\). Wówczas środek \(S\) masy całego zbioru pokrywa się z barycentrum punktów \(S_1\) i \(S_2\), z masami odpowiednio \(M_1\) i \(M_2\).
Dowód. Przeprowadzimy dowód dla punktów położonych na płaszczyźnie, w wyższych wymiarach jest on analogiczny. Nawiązując do powyższego rysunku, niech \(A_1,A_2,\ldots,A_k\) należą do niebieskiego zbioru, a punkty \(A_{k+1},A_{k+2},\ldots,A_n\) do zielonego. Wówczas barycentra \(S_1=(X_1,Y_1)\) i \(S_2=(X_2,Y_2)\) tych zbiorów są punktami
\begin{align*}
S_1 & = \left(\frac{m_1x_1+m_2x_2+\ldots+m_kx_k}{m_1+m_2+\ldots+m_k}, \; \frac{m_1y_1+m_2y_2+\ldots+m_ky_k}{m_1+m_2+\ldots+m_k}\right), \\
S_2 & = \left(\frac{m_{k+1}x_{k+1}+m_{k+2}x_{k+2}+\ldots+m_nx_n}{m_{k+1}+m_{k+2}+\ldots+m_n}, \; \frac{m_{k+1}y_{k+1}+m_{k+2}y_{k+2}+\ldots+m_ny_n}{m_{k+1}+m_{k+2}+\ldots+m_n}\right),
\end{align*}a ich masy całkowite to
\[M_1=m_1+m_2+\ldots+m_k, \qquad M_2 = m_{k+1}+m_{k+2}+\ldots+m_n.\]
Zwróćmy uwagę, że te sumy występują w mianownikach współrzędnych punktów \(S_1\) i \(S_2\). Środkiem masy punktów \(S_1\) i \(S_2\) jest punkt
\[\left(\frac{M_1X_1+M_2X_2}{M_1+M_2},\; \frac{M_1Y_1+M_2Y_2}{M_1+M_2}\right).\]
Wystarczy teraz zauważyć, że
\begin{align*}
\frac{M_1X_1+M_2X_2}{M_1+M_2} & = \frac{M_1\cdot\frac{m_1x_1+m_2x_2+\ldots+m_kx_k}{M_1}+M_2\cdot\frac{m_{k+1}x_{k+1}+m_{k+2}x_{k+2}+\ldots+m_nx_n}{M_2}}{M_1+M_2} \\
& = \frac{m_1x_1+m_2x_2+\ldots+m_nx_n}{m_1+m_2+\ldots+m_n}
\end{align*}i podobnie dla drugiej współrzędnej. Zatem współrzędne barycentrum punktów \(S_1\) i \(S_2\) pokrywają się ze współrzędnymi barycentrum całego (czerwonego) zbioru punktów.
Prawdziwe jest również uogólnienie tego twierdzenia, w którym dany zbiór zamiast na dwa podzbiory dzielimy na trzy lub więcej. Dowód jest podobny, więc pozostawiamy go czytelnikowi.
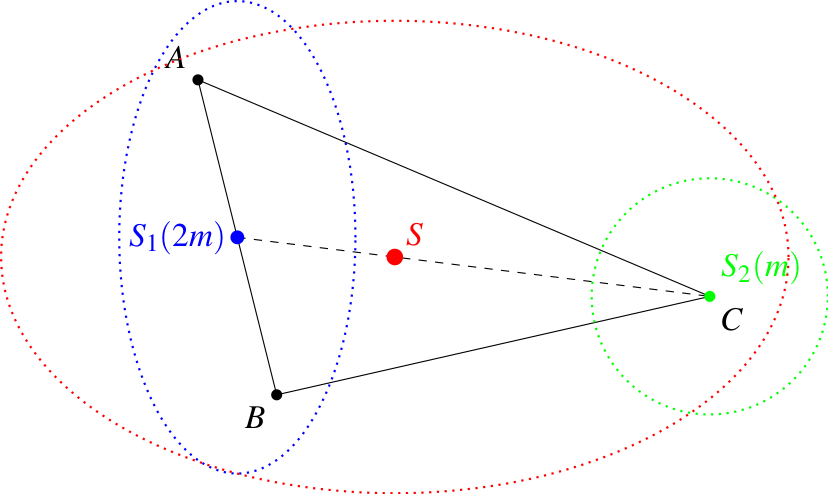
Aby zademonstrować siłę tego twierdzenia, popatrzmy jeszcze raz na środek ciężkości trójkąta \(ABC\), czyli barycentrum punktów \(A\), \(B\) i \(C\) o jednakowej masie \(m\). Niech \(A\) i \(B\) stanowią pierwszy (niebieski) podzbiór, a pojedynczy punkt \(C\) − drugi (zielony). Środkiem \(S_1\) niebieskiego układu jest środek odcinka \(AB\), cały układ ma masę \(2m\). Środkiem zielonego układu jest punkt \(S_2=C\), cały układ ma masę \(m\).
Wobec tego oraz na mocy twierdzenia 1, środek \(S\) ciężkości trójkąta leży na środkowej \(CS_1\) boku \(AB\), w dodatku spełnia warunek \(\frac{|CS|}{|SS_1|}=\frac{2m}{m}=2\).
Takie samo rozumowanie można przeprowadzić dla każdej środkowej, co doprowadzi do następującego wniosku: środkowe w trókącie przecinają się w jednym punkcie i dzielą się w stosunku \(2:1\), licząc od wierzchołków.
Czytelnikowi chcącemu nabrać nieco wprawy pozostawiamy następujące ćwiczenie. W wierzchołkach czworokąta \(ABCD\) umieszczono jednakowe masy. Udowodnić, że ich barycentrum jest środkiem równoległoboku Varignona − którego wierzchołkami są środki boków tego czworokąta.
Współ…
Przed nami najlepsze. Twierdzenia, o którym była mowa w poprzednim rozdziale, wcale nie będziemy używać do wyznaczania środka ciężkości! Jest ono wyśmienitym narzędziem do wykazywania współliniowości punktów i współpękowości prostych.
Wnioski z twierdzenia 1:
- Niech \(S\) będzie barycentrum pewnego zbioru punktów z masami. Podzielmy ten zbiór na dwa podzbiory, jeden o środku masy \(S_1\), drugi − \(S_2\). Wówczas punkty \(S_1\), \(S\) i \(S_2\) leżą na jednej prostej (są współliniowe).
- Jeśli zbiór z poprzedniego punktu jest dość duży, to możemy podzielić go na dwa podzbiory na wiele sposobów. Każdy podział wyznaczy nam pewną prostą. Wszystkie otrzymane w ten sposób proste przechodzą przez jeden punkt (są współpękowe), a punktem tym jest \(S\).
Klasycznym przykładem zastosowania tych wniosków jest następujące twierdzenie, odwrotne do twierdzenia Cevy.
Twierdzenie 2. Na bokach \(BC\), \(CA\) i \(AB\) trójkąta \(ABC\) wybrano odpowiednio punkty \(P\), \(Q\) i \(R\). Jeśli zachodzi równość
\[|AR|\cdot|BP|\cdot|CQ| = |AQ|\cdot|BR|\cdot|CP|,\]to odcinki \(AP\), \(BQ\) i \(CR\) przecinają się w jednym punkcie.
Równość z twierdzenia wygląda na pierwszy rzut oka dziwnie. Dlatego warto w tym momencie spojrzeć na rysunek i uświadomić sobie, że po lewej stronie znaku równości stoi iloczyn długości czerwonych odcinków, a z prawej niebieskich. Zatem ta równość to po prostu \(a_1b_1c_1=a_2b_2c_2\).
Dowód. Niech \(p=a_1b_1c_1=a_2b_2c_2\). Umieśćmy w punkcie \(A\) masę \(m_A=b_1c_2\), w punkcie \(B\) masę \(m_B=b_1c_1\) i w punkcie \(C\) masę \(m_C=b_2c_2\). Zachodzą wówczas równości
\begin{align*}
\frac{m_A}{m_B} & = \frac{b_1c_2}{b_1c_1} = \frac{c_2}{c_1} = \frac{|BR|}{|AR|}, \\
\frac{m_A}{m_C} & = \frac{b_1c_2}{b_2c_2} = \frac{b_1}{b_2} = \frac{|CQ|}{|AQ|}, \\
\frac{m_B}{m_C} & = \frac{b_1c_1}{b_2c_2} = \frac{p/a_1}{p/a_2} = \frac{a_2}{a_1} = \frac{|CP|}{|BP|}.
\end{align*}Z pierwszej równości wnioskujemy, że punkt \(R\) jest barycentrum punktów \(A\) i \(B\). Wobec tego środek masy punktów \(A\), \(B\) i \(C\) leży na odcinku \(CR\). Analogicznie dowodzimy, że ów środek leży na odcinkach \(AP\) i \(BQ\), czyli wszystkie trzy przecinają się w jednym punkcie − barycentrum punktów \(A\), \(B\) i \(C\).
Ciekawy rezultat daje umieszczenie w punktach \(A\), \(B\) i \(C\) mas proporcjonalnych do długości przeciwległych boków trójkąta, odpowiednio \(a=|BC|\), \(b=|CA|\) i \(c=|AB|\). Wówczas \(\frac{|AR|}{|RB|}=\frac{b}{a}\), czyli \(CR\) jest dwusieczną kąta \(ACB\). Analogicznie jest dla \(AP\) i \(BQ\), więc barycentrum tego układu jest środkiem okręgu wpisanego w trójkąt. Jeśli przyjmiemy oznaczenia \(A=(x_A,y_A)\), \(B=(x_B,y_B)\) i \(C=(x_C,y_C)\), to środkiem okręgu wpisanego w trójkąt jest punkt
\[I = \left(\frac{ax_A+bx_B+cx_C}{a+b+c}, \frac{ay_A+by_B+cy_C}{a+b+c}\right).\]
Ale przecież…
W poprzednich rozdziałach badaliśmy obiekty będące skończonymi zbiorami punktów. W życiu codziennym niewiele takich napotkamy. Można mówić o barycentrum wielokąta czy wielościanu, ale trzeba w tym celu zmienić nieco podejście.
Zostańmy jeszcze chwilę na płaszczyźnie. Wyobraźmy sobie, że badana przez nas figura jest zbudowana z jednorodnej, bardzo cienkiej płytki. W tej sytuacji jej masa nie jest rozmieszczona punktowo − masa kawałka płytki jest proporcjonalna do pola powierzchni tego kawałka.
W jaki sposób wyznaczyć teraz barycentrum? Metoda liczenia średniej ważonej oczywiście zawodzi. Jednak w pewnych przypadkach jesteśmy w stanie odpowiedzieć bez zastanowienia − jest jasne, w którym punkcie znajduje się środek masy jednorodnej płytki w kształcie koła, albo prostokąta. Ponadto w mocy pozostaje twierdzenie 1, choć nie będziemy tu tego dowodzić.
Poniższe twierdzenie dotyczy barycentrum jednorodnej płytki trójkątnej. Dzięki niemu będziemy mogli znaleźć środek masy dowolnego wielokąta, dzieląc go na trójkąty i stosując twierdzenie 1.
Twierdzenie 3. Środek masy jednorodnej płytki w kształcie trójkąta \(ABC\) pokrywa się z barycentrum punktów \(A\), \(B\) i \(C\), wziętych z jednakowymi masami.
Innymi słowy, wszystkie te punkty są po prostu znanym ze szkoły środkiem ciężkości trójkąta, co tłumaczy stosowanie tylko tego jednego terminu. W dowodzie będziemy korzystać z pewnej własności barycentrum, którą przyjmujemy za pewnik: jeśli dwa trójkąty są podobne, to środki ich mas zachowują to podobieństwo.
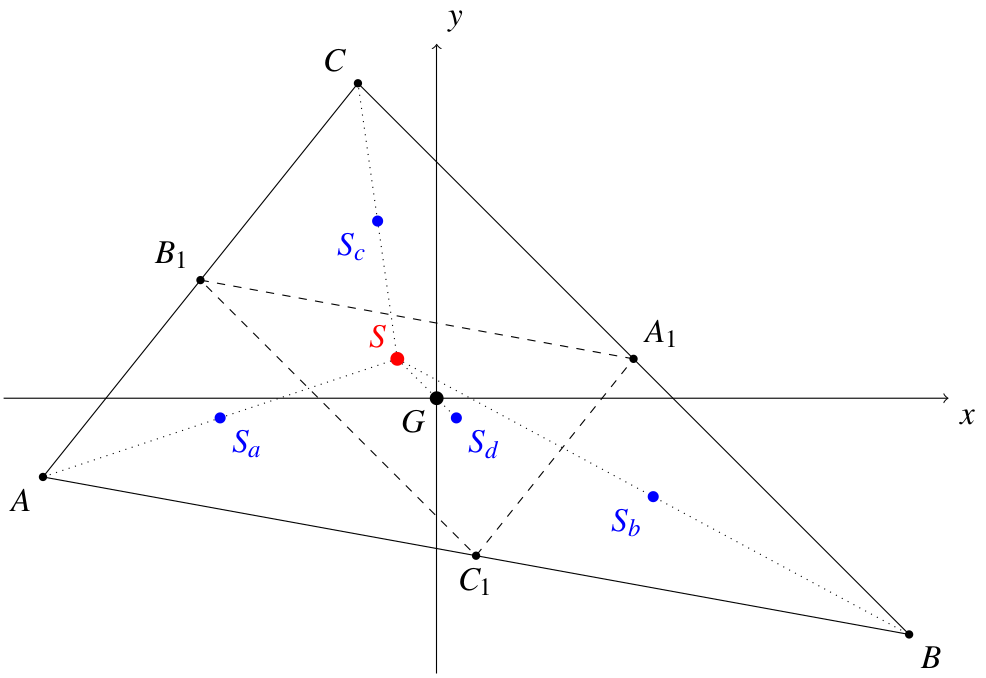
Dowód. Umieśćmy trójkąt o wierzchołkach \(A=(x_A,y_A)\), \(B=(x_B,y_B)\) i \(C=(x_C,y_C)\) w takim układzie współrzędnych, że jego środek ciężkości znajduje się w punkcie \((0,0)\), czyli
\[G = \left(\frac{x_A+x_B+x_C}3, \; \frac{y_A+y_B+y_C}3\right) = (0,0),\]równoważnie \(x_A+x_B+x_C=y_A+y_B+y_C=0\).
Niech \(S=(x,y)\) będzie środkiem masy płytki trójkątnej \(ABC\). Podzielmy ten trójkąt na cztery mniejsze, podobne do niego w skali \(\frac12\), łącząc środki jego boków. Wyznaczymy punkt \(S\) przy użyciu rozszerzonej wersji twierdzenia 1. Poniższy rysunek celowo jest przekłamany, aby uwidocznić, w jaki sposób określone są poszczególne punkty.
Zastąpimy każdą z czterech jednorodnych płytek \(AB_1C_1\), \(A_1BC_1\), \(A_1B_1C\) i \(A_1B_1C_1\) jej barycentrum (odpowiednio \(S_a\), \(S_b\), \(S_c\) i \(S_d\)), wziętym z masą proporcjonalną do jej powierzchni. Te płytki są przystające, więc ich masy są jednakowe.
Trójkąt \(AB_1C_1\) jest jednokładny do trójkąta \(ABC\) względem punktu \(A\), skala tej jednokładności wynosi \(\frac12\). Stąd punkt \(S_a\) jest środkiem odcinka \(SA\), czyli \(S_a=\left(\frac{x_A+x}2,\frac{y_A+y}2\right)\). Analogicznie jest dla punktów \(S_b\) i \(S_c\). Natomiast trójkąt \(A_1B_1C_1\) jest jednokładny do \(ABC\) w skali \(-\frac12\) względem punktu \(G\), z czego wnioskujemy, że \(S_d=\left(-\frac{x}2,-\frac{y}2\right)\).
Na mocy twierdzenia 1, środek masy płytki \(ABC\) pokrywa się z barycentrum punktów \(S_a\), \(S_b\), \(S_c\) i \(S_d\) o równych masach, czyli jego współrzędne są średnimi arytmetycznymi ich współrzędnych. Stąd
\[x = \frac{\frac{x_A+x}2+\frac{x_B+x}2+\frac{x_C+x}2-\frac{x}2}4 = \frac18(x_A+x_B+x_C) + \frac14x = \frac14x,\]więc \(x=0\). Analogicznie dowodzimy, że \(y=0\), co daje \(S=G\) i kończy dowód.
Inaczej rzecz się ma w przypadku czworokąta. Niech dla ustalenia uwagi będzie to czworokąt wypukły \(ABCD\). Barycentrum punktów \(A\), \(B\), \(C\) i \(D\) o jednakowej masie zazwyczaj wypada w innym miejscu niż barycentrum jednorodnej płytki. Pierwsze z nich jest środkiem równoległoboku Varignona, a drugi − równoległoboku Wittenbauera (\(PQRS\) na rysunku). Uzyskuje się go, dzieląc każdy bok czworokąta na trzy równe części i przedłużając odpowiednie odcinki.
Punkty \(U\) i \(V\) są środkami odcinków odpowiednio \(PY\) i \(QX\), więc środek odcinka \(UV\) (niebieski punkt) jest jednocześnie środkiem równoległoboku \(PQXY\). Ten sam punkt jest środkiem masy trójkąta \(ABC\), gdyż \(|AU|=\frac13|AB|\) i \(|CV|=\frac13|CB|\), więc (twierdzenie Talesa) punkt ten leży w \(\frac23\) środkowej wychodzącej z \(B\). Analogicznie jest dla trójkąta \(ACD\) i równoległoboku \(RSYX\) (zielony punkt).
Zastąpimy trójkąty \(ABC\) i \(ACD\) ich barycentrami, którym nadamy masy proporcjonalne do pól tych trójkątów. Na mocy twierdzenia 1 środek ciężkości jednorodnej płytki \(ABCD\) leży gdzieś na prostej łączącej zielony i niebieski punkt. Nietrudno zauważyć, że jest to prosta łącząca środki odcinków \(PQ\) i \(RS\). Analogicznie można udowodnić, że barycentrum płytki leży na prostej łączącej środki odcinków \(QR\) i \(SP\). Wobec tego jest ono punktem przecięcia obydwu prostych, czyli środkiem równoległoboku \(PQRS\).
Konkluzja jest następująca. Mówiąc o barycentrum jakiejś figury, należy sprecyzować, czy chodzi o barycentrum figury jednorodnej, czy może barycentrum jej wierzchołków z równymi masami punktowymi.
Burza w szklance wody
Na koniec zajmiemy się następującym zagadnieniem, którego autorka pozostaje anonimowa:
Ile wody należy nalać do szklanki, aby środek masy szklanki z wodą był położony jak najniżej?
Pytanie jest bardzo naturalne, gdyż dany przedmiot stoi tym stabilniej, im niżej położony jest środek jego masy, a nikt nie lubi przewracających się szklanek z wodą.
Zaczniemy naturalnie od pustej szklanki. Z łatwością możemy zmierzyć jej masę \(M\), wysokość \(h\) oraz promień denka \(r\). Zakładamy przy tym, że szklanka ma kształt matematycznej powierzchni walca z jedną podstawą, wykonana jest z substancji jednorodnej, a jej ściany są zaniedbywalnie cienkie. Wówczas masa każdego kawałka szklanki jest proporcjonalna do pola powierzchni tego kawałka.
Jest rzeczą jasną, że barycentrum szklanki, zarówno pustej jak pełnej, leży na jej osi obrotu. Interesuje nas zatem tylko jedna współrzędna: wysokość. Denko szklanki ma masę proporcjonalną do \(\pi r^2\), a środek jego masy znajduje się na wysokości \(0\). Masa powierzchni bocznej szklanki jest proporcjonalna do \(2\pi rh\), jej barycentrum znajduje się na wysokości \(\frac12h\). W takim razie barycentrum pustej szklanki jest na wysokości
\[H = \frac{0\cdot\pi r^2 + \frac12h\cdot2\pi rh}{\pi r^2 + 2\pi rh} = \frac{h^2}{r+2h}.\]
Dalej będziemy zakładać, że po prostu znamy \(H\) i \(M\).
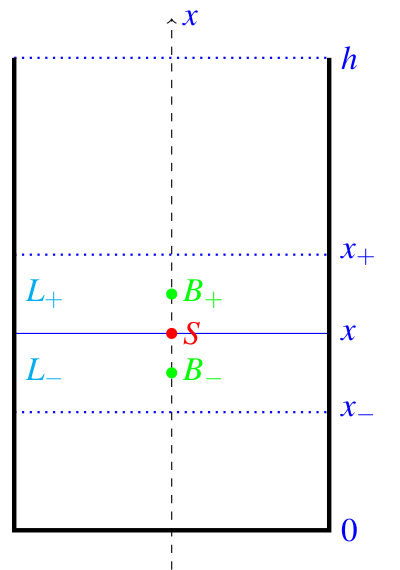
Jeśli nalejemy do szklanki bardzo niewiele wody, to barycentrum układu znajdzie się nad powierzchnią wody. Natomiast dla pełnej szklanki barycentrum układu jest pod powierzchnią wody. W miarę napełniania szklanki położenie barycentrum oraz powierzchni wody zmieniają się w sposób ciągły. Zatem (własność Darboux) w pewnej chwili barycentrum układu znajdzie się na powierzchni wody. Oznaczmy przez \(x\) poziom wody o tej własności.
Niech nadto \(x_-\lt x\lt x_+\). Przez \(S_-\), \(S\) i \(S_+\) oznaczmy barycentra układu szklanki i wody wlanej do poziomu odpowiednio \(x_-\), \(x\) i \(x_+\). Niech \(B_+\) będzie barycentrum samej warstwy \(L_+\) wody pomiędzy poziomami \(x\) i \(x_+\), analogicznie \(B_-\) dla warstwy \(L_-\) pomiędzy \(x_-\) i \(x\).
Układ szklanki z wodą do poziomu \(x_+\) potraktujemy jako sumę układu szklanki z wodą do poziomu \(x\) oraz warstwy \(L_+\). Z tego wnioskujemy, że punkt \(S_+\) leży na odcinku \(SB_+\). Podobnie szklanka z wodą do poziomu \(x\) jest sumą układu szklanki z wodą do poziomu \(x_-\) oraz warstwy \(L_-\), więc punkt \(S\) leży na odcinku \(S_-B_-\). To rozumowanie dowodzi, że \(S_+\) i \(S_-\) są położone wyżej niż \(S\), zatem środek masy układu jest najniżej, gdy znajduje się na powierzchni wody.
Masa wlanej wody, czy jakiejkolwiek innej cieczy, jest równa \(\pi r^2x\rho\), gdzie \(\rho\) oznacza jej gęstość. Dla uproszczenia zapisu przyjmijmy\[A=\frac{M}{\pi r^2\rho},
\]czyli masa cieczy wynosi \(Mx/A\). Barycentrum samej cieczy znajduje się na wysokości \(\frac12x\). W takim razie należy rozwiązać równanie
\[\frac{MH+(Mx/A)\cdot\frac12x}{M+Mx/A}=x,\]które po przekształceniu staje się równaniem kwadratowym \(\frac12x^2+Ax-AH=0\). Jedynym dodatnim rozwiązaniem tego równania jest
\[x = \sqrt{A^2+2AH}-A,\]przy czym \(H\) oznacza wysokość barycentrum szklanki, zaś \(A\) ma ciekawą interpretację fizyczną: jeśli masa wlanej cieczy jest równa masie szklanki, to ciecz, o ile się nie wyleje, sięga do wysokości \(A\).
Takiej szklanki nie przewróci żadna burza!
Artykuł został przygotowany przy wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.