Dla szerokich rzesz nie znających rachunku prawdopodobieństwa prawo wielkich liczb jest czymś ,,magicznym”, czymś, co jest najwyższym prawem rządzącym światem, który nas otacza. Często dwaj dyskutanci głoszący sprzeczne tezy motywują swoje twierdzenia: ,,… bo to wynika z prawa wielkich liczb”. Można by przytoczyć wiele bezsensownych wypowiedzi na temat tego prawa, ale nie to jest celem niniejszego artykułu. Chcemy tutaj wyjaśnić — posługując się pewnym dość ogólnym modelem — treść prawa wielkich liczb.
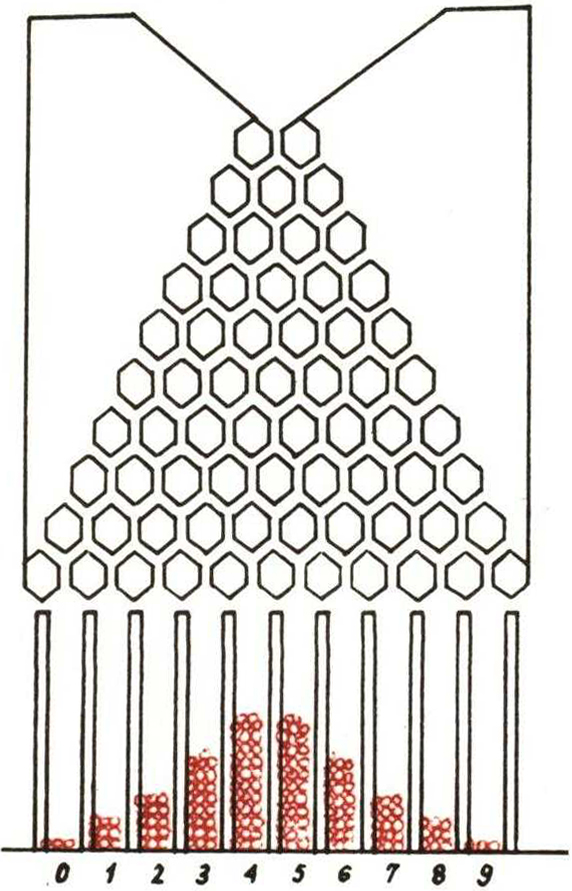
Nie zakładamy, że Czytelnik posiada już jakąś wiedzę z rachunku prawdopodobieństwa, lub co więcej, że zna program tego przedmiotu dla IV klasy liceum. Skoncentrujmy uwagę na doświadczeniu polegającym na rzucaniu ziarenek śrutu na przyrząd zwany deską Galtona (Galton — angielski przyrodnik 1822—1911).
W górne wejście pochylonej deski sypiemy śrut. Kulki wpadają w system kanalików K, biegnących pomiędzy sześciokątnymi wysepkami. Kulka, która znajduje się w położeniu \(x\), może następnie wpaść albo w kanalik prawy \(a\), albo w lewy \(a’\). Można założyć, że obie możliwości są jednakowo prawdopodobne. Zanim kulka wpadnie do jednej z przegródek na dole, to sytuacja ta powtórzy się 9 razy, tj. kulka musi ,,wybrać” dziewięć razy kanalik \(a\) lub \(a’\). Jeżeli kulka 9 razy wybierze kanalik \(a’\), to wpadnie do szufladki o numerze 0, jeżeli dokładnie raz wybierze kanalik \(a\) (obojętnie, w którym momencie), a pozostałe 8 razy kanalik \(a’\), to wpadnie do przegródki o numerze 1, itd; wreszcie, jeżeli za każdym razem wybierze kanalik \(a\), to wpadnie do przegródki numer 9. Każdą drogę prowadzącą do przegródki o numerze \(k\) (\(k = 0, 1,\dots, 9\)) można utożsamić z ciągiem dziewięciowyrazowym o wyrazach \(a\) lub \(a’\). Wszystkich takich ciągów jest \(\binom{9}{k}\), a więc tyleż jest różnych dróg prowadzących do przegródki \(k\). Liczba wszystkich możliwych dróg równa jest 29 (= liczbie wszystkich dziesięciowyrazowych ciągów o wyrazach \(a\) lub \(a’\)). Oznaczmy stosunek liczby wszystkich dróg prowadzących do szufladki \(k\) do liczby wszystkich dróg w ogóle przez \(P_9 (k)\):
\[
P_9(k) = \frac{\binom{9}{k}}{2^9}.
\]
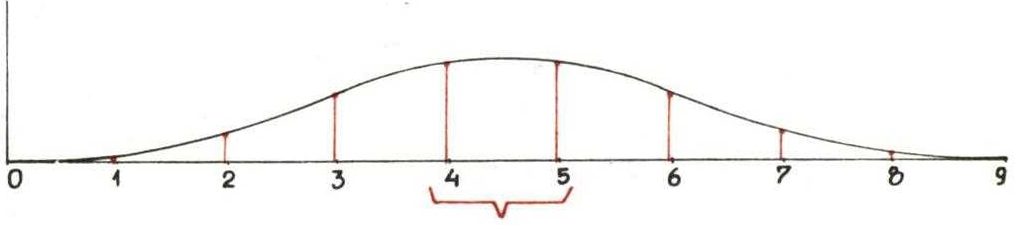
Można przyjąć, że każda droga, licząc średnio, pojawia się tak samo często (bo dlaczego pewne drogi miałyby być bardziej uprzywilejowane, jeżeli całe urządzenie jest zrobione dostatecznie precyzyjnie?). Zatem liczba \(P_9(k)\) powinna być niemal równa częstości wpadania kulki do przegródki \(k\), o ile rozpatrujemy dostatecznie wiele prób polegających na puszczaniu ziarenek śrutu. Liczbę \(P_9(k)\) nazwiemy prawdopodobieństwem trafienia kulki do przegródki \(k\). Przedstawmy graficznie wartości \(P_9(k)\). Na osi \(0X\) prowadzimy z każdego punktu o odciętej \(k = 0, 1, \dots, 9\) odcinek prostopadły do osi \(OX\) o długości \(P_9(k)\) i łączymy linią ciągłą wierzchołki tych odcinków.
Widać, że prawdopodobieństwo \(a_9\) trafienia kulki w przegródki o numerach 4 lub 5 (= sumie długości odcinków prowadzonych z punktów o odciętych 4 i 5) jest równe 0,492. Oznacza to, że średnio co druga kulka wpada w jedną z przegródek o numerach 4 lub 5, a przecież stanowią one tylko 20\% wszystkich przegródek.
A jak wygląda sytuacja, jeśli rozważyć deskę Galtona z 20 przegródkami (to znaczy z 19 rzędami wysepek, co oznacza, że kulka 19 razy ,,wybiera” drogę)? Analogicznie jak poprzednio, parawdopodobieństwa \(P_{19}(k)\) dotarcia kulki do przegródki o numerze \(k\) określone są wzorami:
\[
P_{19}(k) = \frac{\binom{19}{k}}{2^{19}},\quad k=0,1,\dots,19.
\]
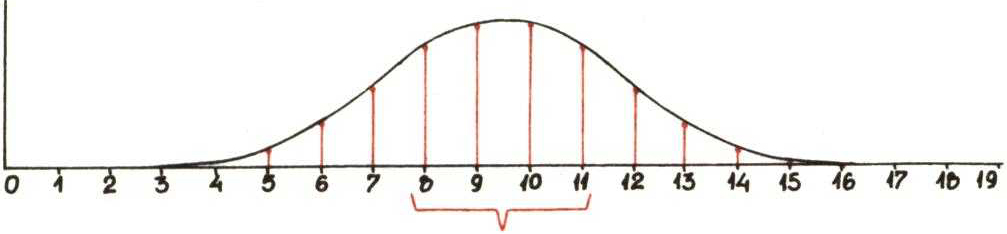
Graficzny obraz liczb \(P_{19}(k)\) jest następujący:
Przegródki o numerach 8, 9, 10, il stanowią dokładnie 20\% wszystkich przegródek. Oznaczmy przez a19 prawdopodobieństwo, że ziarenko śrutu trafi do jednej z tych 4 przegródek. Będzie ono sumą prawdopodobieństw, że ziarenko trafi odpowiednio do przegródek 8, 9, 10 i 11. Łatwo obliczyć, że \(a_{19} = 0{,}64\). W przybliżeniu oznacza to, że średnio na każde 3 ziarenka śrutu 2 trafiają do tych 20\% przegródek, a tylko 1 do pozostałych 80\%.
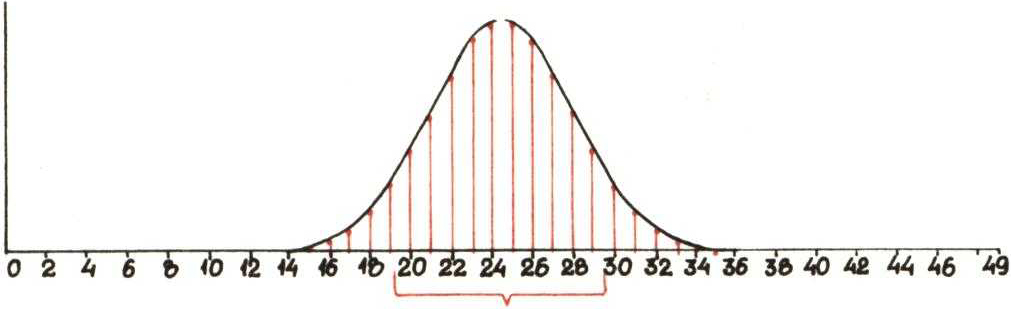
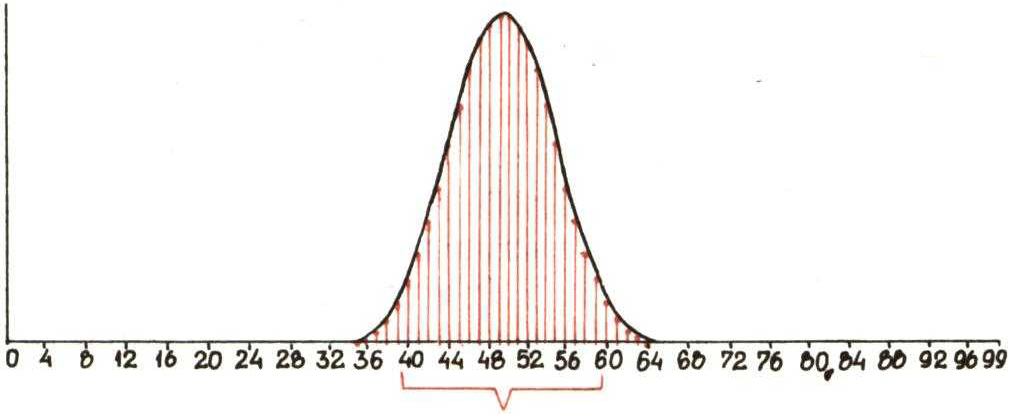
W przypadkach desek Galtona z 50 i 100 przegródkami wykresy są następujące:
Na każdym z wykresów zaznaczono klamrą 20\% przegródek, tych o największych prawdopodobieństwach. Oznaczmy odpowiednio przez \(a_{49}\) i \(a_{99}\) prawdopodobieństwa, że ziarenko śrutu trafi do jednej z tych przegródek. Można obliczyć, że
\[
a_{49} = 0{,}834,\quad a_{99} = 0{,}966.
\]
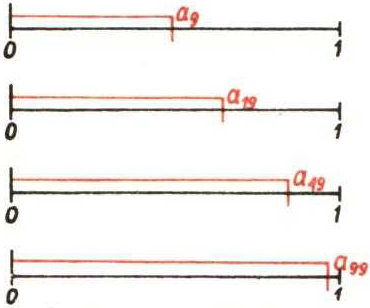
Przyjrzyjmy się liczbom \(a_{n}\) dla \(n = 9, 19, 49, 99\): w odcinku o długości 1 będziemy odkładali odcinki o długościach \(a_n\):
Nasuwa się przypuszczenie, że wraz ze wzrostem \(n\) prawdopodobieństwo \(a_n\) trafienia w jedną z 20\% środkowych przegródek wzrasta do 1, a tym samym prawdopodobieństwo trafienia w jedną z pozostałych 80\% maleje do 0.
Tych 20\% środkowych przegródek są to przegródki o numerach \(k\), spełniających warunek
\[
\left| k-\frac{n}{2} \right| \leq \frac{1}{5}n.
\]
Oznaczmy przez \(S_n\) liczbę zakrętów ,,w prawo” wykonanych przez pojedynczą spadającą kulkę. Zdarzenie, że kulka trafi w jedną ze środkowych przegródek, polega na tym, iż kulka ta potoczy się taką drogą, że
\[
\left| S_n-\frac{n}{2} \right| \leq \frac{1}{5}n\quad \text{(*)}.
\]
Nasze przypuszczenie można więc wyrazić następująco: w ciągu \(n\) jednakowo prawdopodobnych losowań ,,w prawo” lub ,,w lewo” (\(a\) lub \(a’\)) prawdopodobieństwo wylosowania drogi o \(S_n\) spełniającym (*) dąży do 1. Prawdopodobieństwo zdarzenia definiowaliśmy jako granicę częstości pojawiania się tego zdarzenia przy liczbach prób dążących do nieskończoności. A zatem zdarzenia o prawdopodobieństwach bliskich 1 należy tłumaczyć sobie jako bardzo częste (prawie zawsze). Czyli, praktycznie biorąc, dla dużych \(n\) prawie na pewno liczba \(S_n\) musi spełniać warunek (*). Liczba \(\frac{1}{5}\) (owe 20\%) nie jest tu uprzywilejowana; te same rozważania z tymi samymi rezultatami można przeprowadzić zastępując liczbę \(\frac{1}{5}\) dowolną liczbą \(\varepsilon > 0\).
W naszej desce Galtona losowania ,,w prawo” i ,,w lewo” były jednakowo prawdopodobne. Gdybyśmy skonstruowali deskę taką, że zdarzenia ,,w prawo” i ,,w lewo” nie są jednakowo prawdopodobne, na przykład prawdopodobieństwo, że kulka potoczy się w prawo, jest równe \(p\), prawdopodobieństwo, że potoczy się w lewo, jest równe \(q\), \(p \not = q\), \(p + q = 1\), to nie wnikając w szczegóły techniczne doszlibyśmy do następującego wniosku: prawdopodobieństwo zdarzenia, że w ciągu \(n\) losowań kanalików \(a\) i \(a’\) liczba \(S_n\) wylosowanych wyrazów a spełnia warunek
\[
|S_n-n\cdot p| \leq n\cdot \varepsilon,\quad (**)
\]
dąży do 1; \(\varepsilon\) jest tutaj dowolną, ustaloną liczbą dodatnią.
Praktycznie oznacza to, że dla dużych \(n\) nierówność (**) jest spełniona prawie na pewno. Zazwyczaj nierówność (**) zapisujemy w postaci:
\[
\left|\frac{S_n}{n}-p\right|\leq \varepsilon
\]
Sformułowany powyżej wniosek został po raz pierwszy zaobserwowany i udowodniony przez szwajcarskiego matematyka Jakuba Bernoulli (1654—1705). Wniosek ten nosi nazwę ,,prawo wielkich liczb Bernoulliego”. Jest to historycznie pierwsze twierdzenie z cyklu twierdzeń nazywanych prawami wielkich liczb. Oczywiście losowania dróg ,,w prawo” i ,,w lewo” można zastąpić losowaniem orła i reszki przy rzucie monetą, losowaniem szóstki lub nie-szóstki przy rzucie kostką, wreszcie samo losowanie można zastąpić procesem porodu, a rezultaty ,,w prawo”, ,,w lewo” — płcią noworodka: ,,chłopiec”, ,,dziewczynka”. Są to tylko zmiany typu interpretacyjnego, sama matematyczna istota zagadnienia pozostaje nie zmieniona.
Prawo wielkich liczb wypowiada się tylko na temat granicy prawdopodobieństw pewnych zdarzeń, nie wyklucza więc ono możliwości zdarzeń takich, w których pojawiają się długie serie ,,w prawo” lub ,,w lewo”. Nie należy także wnioskować, że zdarzenia ,,w prawo” i ,,w lewo” muszą się na ogół przeplatać lub też że liczby ich w ciągu o parzystej liczbie wyrazów (oznaczmy ją przez \(2n\)) muszą być równe. Wręcz odwrotnie, gdy \(n\) dąży do nieskończoności, to prawdopodobieństwa te maleją do O szybciej niż ciąg \(\frac{1}{\sqrt{n}}\). Zainteresowanego Czytelnika odsyłamy tu do podręcznika z rachunku prawdopodobieństwa dla klasy IV liceum. O zastosowaniu prawa wielkich liczb będziemy mówić w następnym artykule.
Artykuł został pierwotnie opublikowany w miesięczniku Delta w nr. 11 w 1974 roku. Poznańska Fundacja Matematyczna otrzymała zgodę na umieszczenie tekstu. Przygotowanie cyfrowej wersji artykułu został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.