Pojęcie bazy Schaudera
Rozważamy zbiór wszystkich funkcji ciągłych określonych na przedziale $[0,1]$ i o wartościach w zbiorze liczb rzeczywistych. Zazwyczaj zbiór ten oznacza się symbolem $C[0,1]$ (litera $C$ pochodzi od słowa „ciągły” – „continuous”). Zbiór $C[0,1]$ ma tę właściwość, że jeżeli dodamy do siebie skończoną liczbę dowolnych funkcji z tego zbioru pomnożonych przez dowolne liczby rzeczywiste, to znów otrzymamy funkcję należącą do zbioru $C[0,1]$. Zbiory o takich własnościach nazywa się przestrzeniami liniowymi funkcji, skończone sumy funkcji pomnożonych przez pewne liczby – kombinacjami liniowymi funkcji.
Chcemy teraz wskazać pewien nieskończony podzbiór zbioru $C[0,1]$ taki, że dowolną funkcję ze zbioru $C[0,1]$ możemy z dowolną dokładnością przybliżyć przez kombinację liniową funkcji z tego podzbioru. Podzbiór, który wskażemy, nosi nazwę \textit{bazy Schaudera} przestrzeni liniowej $C[0,1]$ i został podany w 1927 roku przez polskiego matematyka Juliusza Schaudera. Można sobie wyobrażać, że przestrzeń liniowa $C[0,1]$ jest zbudowana z nieskończonej liczby dobrze określonych „atomów”, tak jak nasz świat materialny składa się z atomów (jest to tylko analogia i jak każda analogia ma swoje granice…).
Funkcje bazowe
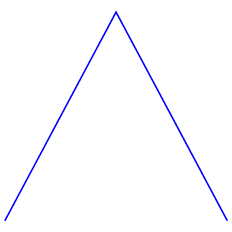
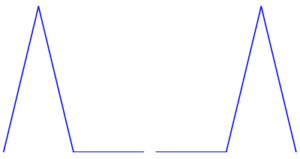
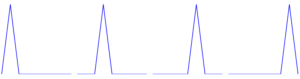
Nasze „atomy” będziemy oznaczać symbolem $s_{n,k}$, gdzie $n$ jest dowolną nieujemną liczbą całkowitą, a $k$ dla danego $n$ jest jedną z liczb całkowitych $0,\dots, 2^n -1$. Aby pomóc wyobraźni, można sobie powiedzieć, że $n$ oznacza „pokolenia”, a $k$ kolejne „dzieci” w danym pokoleniu. A zatem w zerowym pokoleniu mamy tylko jednego „rodzica” $s_{0,0}$; z pierwszym pokoleniu są dwoje dzieci $s_{1,0}$ i $s_{1,1}$; w drugim pokoleniu jest czworo dzieci $s_{2,0}$, $s_{2,1}$, $s_{2,2}$ i $s_{2,3}$; w trzecim ośmioro dzieci $s_{3,0}$, $s_{3,1}$, $s_{3,2}$, $s_{3,3}$, $s_{3,4}$, $s_{3,5}$, $s_{3,6}$ oraz $s_{3,7}$; i tak dalej. A oto wykres przedstawiający, jak chcemy zdefiniować poszczególne funkcje należące do bazy Schaudera.
![]()
Jak widzimy, wszystkie funkcje łączy wielkie podobieństwo: wyglądają jak indiańskie wigwamy o zawsze tej samej wysokości, ale o w każdym kolejnym pokoleniu „szczuplejsze” o połowę i z „czubkiem”, który przesuwa się w sposób regularny. Czasami mówi się o nich „funkcje daszkowe” lub „funkcje namiotowe”. Funkcje te mają wartość zero poza przedziałami, gdzie „stoi” wigwam. Te przedziały to
\begin{align*}
[0,1]
\end{align*}
\begin{align*}
[0,\frac{1}{2}] \quad\quad [\frac{1}{2},1]
\end{align*}
\begin{align*}
[0,\frac{1}{4}]\quad \quad [\frac{1}{4},\frac{2}{4}]\quad \quad [\frac{2}{4},\frac{3}{4}] \quad \quad [\frac{3}{4},1]
\end{align*}
i tak dalej.
A wierzchołki wigwamów znajdują się w punktach
\begin{align*}
\frac{1}{2}
\end{align*}
\begin{align*}
\frac{1}{4}\quad \quad \frac{3}{4}
\end{align*}
\begin{align*}
\frac{1}{8}\quad \quad \frac{3}{8} \quad \quad \frac{5}{8} \quad\quad \frac{7}{8}
\end{align*}
i tak dalej.
Przedziały $[\frac{k}{2^n},\frac{k+1}{2^n}]$ i ich środki $\frac{k+1/2}{2^n}$, gdzie $k=0,\dots,2^n-1$, spotyka się tak często w matematyce, że otrzymały one nazwy: przedziały i liczby diadyczne.
Do tego zbioru funkcji dorzucimy jeszcze funkcję stałą $\chi(x)=1$ i funkcję $\ell(x)=x$.

W ten sposób otrzymaliśmy ciąg funkcji ciągłych (pierwszą funkcją jest $\chi$, potem jest $\ell$, dalej $s_{0,0}$, $s_{1,0}$, $s_{1,1}$, $s_{2,0}$ i tak dalej) charakteryzujący się tym, że każda funkcja ma taki punkt, w którym przyjmuje wartość $1$ i w którym wszystkie następne funkcje przyjmują wartość $0$. Stąd wynika, że żadnej funkcji z naszego ciągu nie można otrzymać jako liniowej kombinacji pozostałych funkcji.
Przybliżanie funkcji przez funkcje bazowe
Pokażemy teraz, w jaki sposób można przybliżać dowolną funkcję $f$ z przestrzeni liniowej $C[0,1]$ przez kombinacje liniowe „atomów” z naszego ciągu funkcji. Zrobimy to na konkretnym przykładzie funkcji $f(x)=-1 + 2 x^2 + \sin 5 x$.
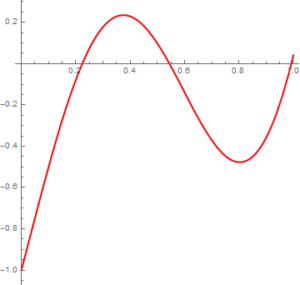
Najpierw utworzymy taką kombinację liniową funkcji $\chi$ i $\ell$, aby wartości funkcji $f$ i tej kombinacji liniowej były takie same w punktach $x=0$ i $x=1$. Wystarczy w tym celu znaleźć współczynniki liczbowe $a$ o $b$ kombinacji liniowej, rozwiązując układ równań
$$\left\{
\begin{array}{ll}
f(0)=a\chi(0)+b\ell(0) \\
f(1)=a\chi(1)+b\ell(1),
\end{array}
\right.$$
czyli
$$\left\{
\begin{array}{ll}
f(0)=a\\
f(1)=a+b.
\end{array}
\right.$$
Znajdujemy, że $a=f(0)$, a $b=f(1)-f(0)$, a więc wstępnym przybliżeniem funkcji $f$ jest funkcja $f_0(x)=f(0)\chi(x)+[f(1)-f(0)]\ell(x)$, która zgadza się z funkcją $f$ w punktach $0$ i $1$.
Różnica między funkcją $f$ a jej wstępnym przybliżeniem jest równa $g_0(x)=f(x)-f_0(x)$.
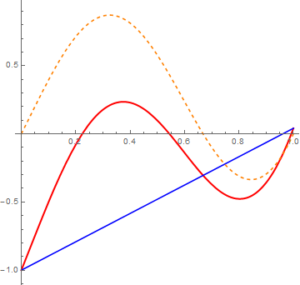
Następnie chcielibyśmy użyć do przybliżania także funkcji $s_{0,0}$, aby uzyskać przybliżenie pokrywające się z funkcją $f$ w punktach $0$, $1$ i $\frac{1}{2}$. Zrobimy to w ten sposób, że przybliżymy funkcję $g_0$, czyli różnicę funkcji $f$ i wstępnego przybliżenia $f_0$, za pomocą funkcji $h_0(x)=g_0(\frac{1}{2})s_{0,0}(x)$. Zauważmy, że funkcja $h_0$ zgadza się z funkcją $g_0$ w punktach $0$, $1$ i $\frac{1}{2}$, a to oznacza, że funkcja $f_1(x)=f_0(x)+h_0(x)$ zgadza się w tych samych punktach z funkcją $f$ i funkcja $f_1$ jest naszym następnym przybliżeniem.
Poniższy wykres przestawia funkcje $f$, $f_1$ i $g_1(x)=f(x)-f_1(x)$.
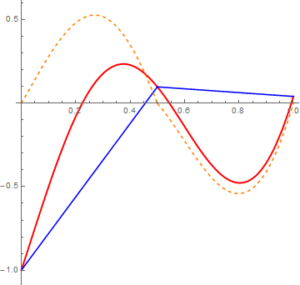
Z kolei chcemy uwzględnić w przybliżeniu funkcji $f$ także funkcje z następnego pokolenia funkcji bazowych. Najpierw przybliżamy poprzednią różnicę $g_1(x)=f(x)-f_1(x)$ za pomocą funkcji $h_1(x)=g_1(\frac{1}{4})s_{1,0}+g_1(\frac{3}{4})s_{1,1}$. Funkcje $g_1$ i $h_1$ zgadzają się w punktach $0$, $1$, $\frac{1}{2}$, $\frac{1}{4}$, $\frac{3}{4}$, co oznacza, że funkcja $f_2(x)=f_1(x)+h_1(x)=f_0(x)+h_0(x)+h_1(x)$ w tych samych punktach zgadza się z funkcją $f$. Funkcja $f_2$ jest naszym nowym przybliżeniem.
Wykres przestawia funkcje $f$, $f_2$ i $g_2(x)=f(x)-f_2(x)$. Zwróć uwagę, jak maleje różnica między funkcją $f$ a kolejnymi przybliżeniami.
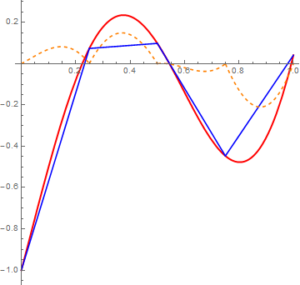
Postępując systematycznie uwzględniamy w naszym przybliżeniu dalsze pokolenia funkcji bazowych. Dla drugiego pokolenia otrzymujemy przybliżenie różnicy $g_2(x)=f(x)-f_2(x)$ za pomocą funkcji $h_2(x)=g_2(\frac{1}{8})s_{2,0}+g_2(\frac{3}{8})s_{2,1}+g_2(\frac{5}{8})s_{2,2}+g_2(\frac{7}{8})s_{2,3}$. Funkcje $g_2$ i $h_2$ zgadzają się w punktach $0$, $1$, $\frac{1}{2}$, $\frac{1}{4}$, $\frac{3}{4}$, $\frac{1}{8}$, $\frac{3}{8}$, $\frac{5}{8}$ i $\frac{7}{8}$, a więc funkcja $f_3(x)=f_2(x)+h_2(x)=f_0(x)+h_0(x)+h_1(x)+h_2(x)$ w tych punktach zgadza się z funkcją $f$.
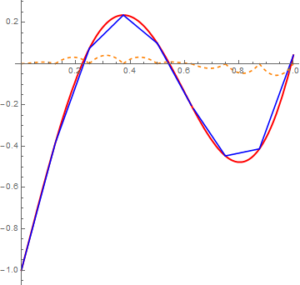
Różnica między funkcją $f$ a jej przybliżeniami stopniowo maleje i możemy dowolnie ją ograniczać. Do budowy przybliżeń wykorzystywaliśmy jedynie funkcje z opisanego na początku ciągu funkcji. Każde uwzględnione pokolenie funkcji bazowych „wysubtelnia” przybliżenie. W granicy otrzymujemy przedstawienie funkcji $f$ z przestrzeni liniowej funkcji ciągłych $C[0,1]$ za pomocą nieskończonej sumy funkcji bazowych przemnożonych przez współczynniki liczbowe. Każda funkcja $f$ z $C[0,1]$ ma tylko jedno takie przedstawienie. Czy widzisz, dlaczego każdy współczynnik liczbowy mogliśmy wybrać tylko w jeden sposób?
Ten artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną z Fundacji mBanku na realizację projektu „Potęga matematyki”.

