W pierwszych latach szkolnej edukacji poznajemy pojęcie funkcji, a jednym z pierwszych omawianych przykładów jest funkcja liniowa. Niniejszy tekst opisuje ciekawe zastosowanie tej prostej funkcji do badania zależności statystycznych.
Metoda statystyczna − elementarz
Praca statystyka zwykle polega na analizie danych rzeczywistych (np. wyników obserwacji pewnego zjawiska). Są to wartości badanej cechy lub cech (zwanych też zmiennymi), które mogą dotyczyć właściwie wszystkiego. Przykładową cechą jest wzrost mieszkańców Poznania, zarobki pracowników danej firmy, wykształcenie mieszkańców danego kraju itd. Jeśli naszym celem jest wyjaśnienie pewnych zależności, które możemy obserwować, musimy poświęcić kilka chwil przed zbieraniem danych (np. w terenie) na pracę umysłową (np. przy biurku).
Przede wszystkim musimy jasno postawić sobie problem który chcemy zbadać, żeby wiedzieć które dane będą nam faktycznie potrzebne. Wyjście w teren i zbieranie danych zawsze wiąże się z kosztami, których (być może) można uniknąć już na etapie planowania. Zapytacie pewnie dlaczego nie można zbierać więcej (a może nawet wszystkich możliwych) danych? Ma to związek z tzw. wielokrotnym pomiarem. Jeśli będziemy zbierać naprawdę dużo danych, zawsze uda nam się znaleźć pewne prawidłowości (w danych), których wcześniej badać nie planowaliśmy. Ich obecność może być tylko przypadkiem, np. wynikającym z przeprowadzenia pomiarów w tym konkretnym momencie. Im więcej pomiarów przeprowadzimy równocześnie, tym większe prawdopodobieństwo, że pewne prawidłowości pojawią się w danych przez przypadek. Jeśli będziemy torturować dane wystarczająco długo, przyznają się do wszystkiego − stwierdził kiedyś dowcipnie amerykański ekonomista George J. Stigler. Tego ,,torturowania” danych metodami statystycznymi staramy się właśnie uniknąć.
Jeśli dane zostały już jednak zebrane i ktoś wysyła je nam do analizy, mamy jeszcze jeden sposób na uniknięcie tego błędu. Zanim spojrzymy na dane powinniśmy zrozumieć, co i w jaki sposób było mierzone, a następnie tylko na tej podstawie spróbować znaleźć matematyczny model (opis wzorami) według którego nasze zjawisko przebiega. Na przykład możemy być przekonani (z różnych socjoekonomicznych powodów), że wydatki rosną liniowo wraz z dochodami (a więc w przybliżeniu spełniają zależność \(y=ax+b\)). Oczywiście każdy model musi mieć możliwość ,,strojenia”, czyli pewną swobodę wyboru konkretnej funkcji − w przykładzie modelu liniowego jest to rzecz jasna swoboda wyboru współczynnika kierunkowego \(a\) i wyrazu wolnego \(b\).
Dlaczego powinniśmy wybrać model zanim spojrzymy na dane? Jeśli celem naszym jest tłumaczenie badanego zjawiska, musimy to zrobić z powodów zewnętrznych, a zebrane dane mogą nasze wytłumaczenie podtrzymać, lub obalić. Dzięki odpowiedniemu wyborowi parametrów możemy ,,dopasować” naszą funkcję do danych, ale tylko w pewnym zakresie (tj. wewnątrz modelu). Na przykład, jeśli wybraliśmy model liniowy, a dane pochodzą ze zjawiska o ,,charakterze kwadratowym”, żaden wybór parametrów \(a\) i \(b\) nie okaże się dobry. Wtedy będziemy zmuszeni odrzucić wybrany model i spróbować swoich sił jeszcze raz − tym razem w oparciu o inny model.
Jak łatwo możemy zauważyć − jeśli model wybierzemy ,,pod dane”, szansa na to, żeby został odrzucony (przez te dane) drastycznie spada1, więc wybór modelu przed oglądaniem danych jest bardzo ważny. Reasumując, statystyka matematyczna funkcjonuje według następującej procedury:
- sformułowanie problemu
- wybór modelu matematycznego
- dobór specyficznych parametrów modelu na podstawie danych
- sprawdzenie czy model przez nas wybrany dobrze przybliża dane.
Dzięki tej kolejności możemy uniknąć sytuacji, w której statystyka staje się ,,samo- sprawdzającą się przepowiednią” — model liniowy wyglądał na dobrze przybliżający nasze dane, więc wybraliśmy model liniowy, który (niespodzianka!) dobrze przybliża dane. Z tego oczywiście nie wynika, że mierzone zjawisko może być wyjaśnione jakąś formą liniowej zależności, tylko, że metoda, którą wybraliśmy na podstawie punktów na płaszczyźnie, dobrze przybliża te konkretne punkty.
W niniejszym artykule rozważymy dane dotyczące dwóch cech: miesięczne dochody w rodzinie w przeliczeniu na jedną osobę (cecha pierwsza), i miesięczna wartość wydatków konsumpcyjnych w rodzinie w przeliczeniu na jedną osobę (cecha druga). Mamy pełne prawo podejrzewać, że pomiędzy tymi cechami istnieje pewna zależność, oraz − z powodów których nie będziemy szerzej omawiać2 (jako że nie jest to część matematyki, tylko socjologii i/lub ekonomi) − przyjmiemy model liniowy zależności między zmiennymi (cechami). Przybliżanie danych funkcją liniową nazywane jest w literaturze regresją liniową. Skupimy się głównie na punkcie trzecim z powyższego schematu, czyli spróbujemy odpowiedzieć na pytanie, w jaki sposób dobrać parametry modelu liniowego, by dobrze przybliżał zebrane dane.
To co pozostaje to interesujący punkt czwarty, który (w dużym uproszczeniu) stanowi podstawę funkcjonowania współczesnych nauk empirycznych. Mianowicie, jak rozstrzygnąć czy zebrane dane obalają model, który wszyscy do tej pory uważali za prawdziwy? Jednak sama odpowiedź na to pytanie zajęłaby więcej miejsca niż możemy przeznaczyć w tej chwili, więc odsuniemy ją do kolejnego artykułu.
Zebrane dane empiryczne
Pomiary dwóch badanych cech (dla dziesięciu rodzin) są podane w poniższej tabeli.
| Nr | Dochody | Wydatki |
|---|---|---|
| 1 | 210 | 140 |
| 2 | 270 | 190 |
| 3 | 290 | 250 |
| 4 | 310 | 270 |
| 5 | 370 | 290 |
| 6 | 400 | 310 |
| 7 | 450 | 340 |
| 8 | 480 | 360 |
| 9 | 510 | 420 |
| 10 | 520 | 390 |
Ponieważ mamy do dyspozycji tylko dziesięć punktów, więc tzw. wykres rozrzutu (czyli nic innego, jak wykres funkcji danej w postaci tabelki) będzie odpowiednio czytelny. Na osi odciętych umieszczamy dochody, zaś na osi rzędnych − wydatki jak na poniższym rysunku.
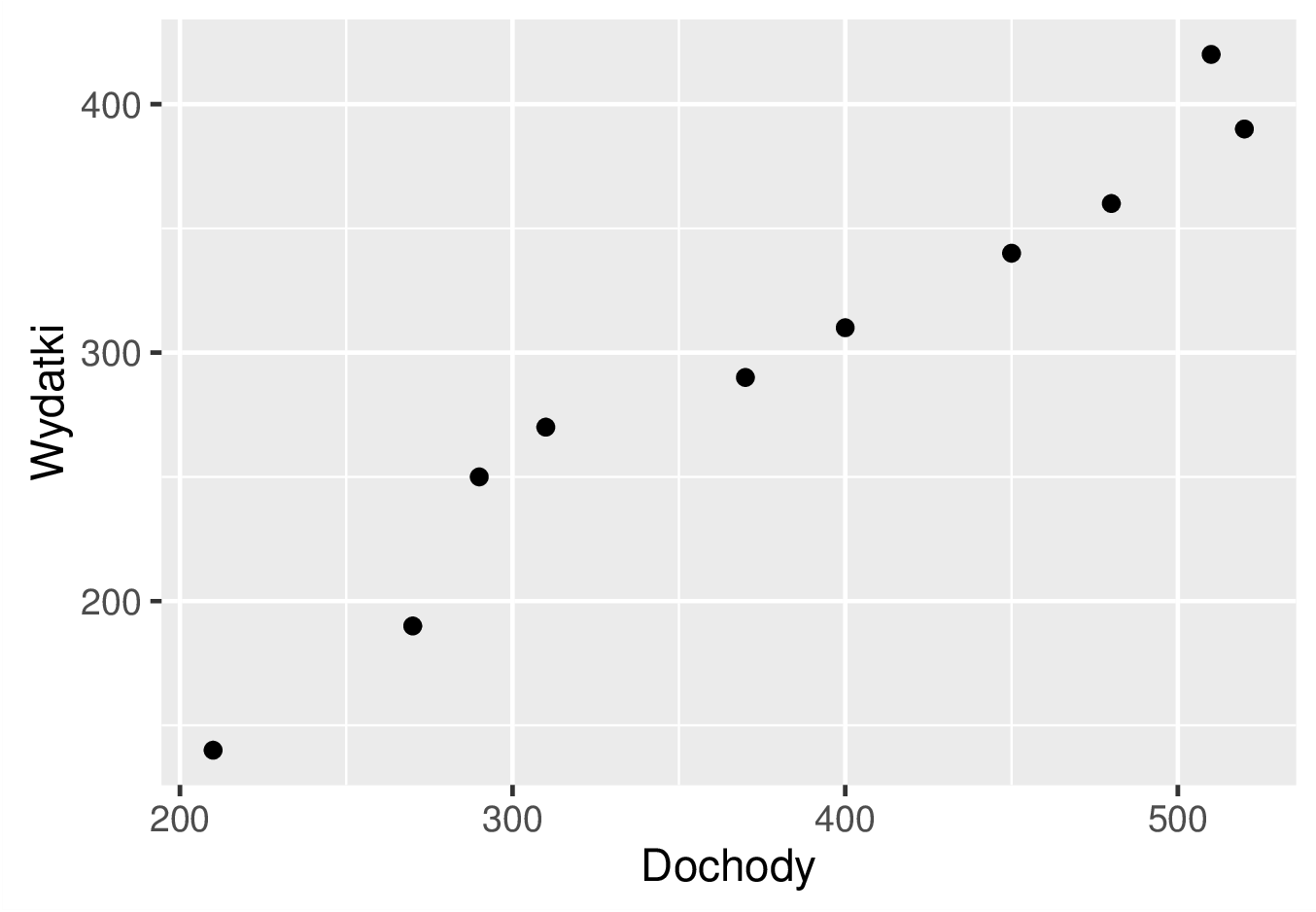
Wykres rozrzutu danych dotyczących miesięcznych dochodów i wydatków konsumpcyjnych w rodzinie w przeliczeniu na jedną osobę
Jak możemy zaobserwować na rysunku, punkty odpowiadające parom z powyższej tabeli układają się wzdłuż pewnej prostej o dodatnim współczynniku kierunkowym, więc wybrany przez nas model (regresja liniowa, którą opiszemy w następnym punkcie) ma szanse dobrze przybliżać wyniki pomiaru. Intuicyjnie oznacza to, że możemy ,,wpisać” pewną funkcję liniową \(f(x)=ax+b\) w nasze dane. W jaki sposób wybrać parametry \(a\) i \(b\) spośród wszystkich możliwych? O tym napiszemy w kolejnym punkcie.
Model regresji liniowej
Jak już powiedzieliśmy w poprzednim punkcie do matematycznego opisu zależności między dochodami a wydatkami wykorzystamy metodę regresji liniowej. Ogólnie termin regresja oznacza metodę pozwalającą na modelowanie związku pomiędzy zmiennymi (cechami) i wykorzystanie tej wiedzy do przewidywania nieznanych wartości jednej zmiennej na podstawie znajomości innych.
Przypomnijmy, że dysponujemy \(n=10\) obserwacjami \(x_1=210,x_2=270,\dots,x_{n}=520\) zmiennej \(x\) oraz odpowiadającymi im obserwacjami \(y_1=140,y_2=190,\dots,y_{n}=390\) zmiennej \(y\) (jak w tabeli 1). Chcielibyśmy opisać zależność między zmiennymi \(x\) i \(y\) za pomocą funkcji liniowej \(y=ax+b\), wykorzystując powyższe obserwacje. Jednak jak wiemy, przez dwa punkty na płaszczyźnie można przeprowadzić dokładnie jedną prostą, ale jak ją przeprowadzić przez dziesięć punktów? W ogólności oczywiście nie można przeprowadzić prostej przez wszystkie punkty naszych danych, więc musimy pogodzić się z faktem, że nasze przybliżenie będzie obarczone pewnym błędem. Czy ten błąd jest winą regresji liniowej? Niekoniecznie.
Powodem tej niedokładności mogą być błędy przypadkowe w danych, np. błędy pomiaru powstające podczas zbierania danych. Błąd wynikający z tego typu niedokładności powinniśmy umieć dosyć dobrze zminimalizować, korzystając z metody najmniejszych kwadratów, którą opisujemy w kolejnym punkcie. Uwaga! Błąd przybliżenia może również wynikać z tego, że w rzeczywistości \(y\) nie zależy liniowo od \(x\), albo co gorsza \(y\) zależy również od innych zmiennych (niż \(x\)) których pomiary nie były zbierane. Oba te przypadki to tzw. błędna specyfikacja modelu (ang. model misspecification) i wówczas (najczęściej) błędu przybliżenia nie uda się wyraźnie zmniejszyć żadnymi metodami.
Nie musimy się jednak ostatnimi dwoma przypadkami martwić, jako że nasze dane zdają się posłusznie leżeć blisko pewnej prostej. Będziemy zatem posługiwać się modelem regresji liniowej danym następującym wzorem
\begin{equation}\label{model}
y_i=ax_i+b,\quad i=1,2,\dots,n,
\end{equation}
gdzie \(a, b\in \mathbb{R}\) są parametrami, które musimy ,,dostroić” do naszych danych3. Jak już wspomnieliśmy jedną z metod ,,strojenia” współczynników modelu jest metoda najmniejszych kwadratów.
Metoda najmniejszych kwadratów
Model regresji liniowej dany wzorem \eqref{model} zależy od nieznanych parametrów \(a\) i \(b\). Szacowanie parametrów modelu statystycznego na podstawie danych nazywa się estymacją, a same oszacowania tych parametrów estymatorami. Estymatory parametrów \(a\) i \(b\) chcemy dobrać tak, aby otrzymać prostą jak najlepiej dopasowaną do obserwacji. Nasze liniowe przybliżenie będzie obarczone błędem (przybliżenia) dla każdej pary \((x_i,y_i)\). Dlatego w dalszej części zajmiemy się jedną z metod minimalizującą te błędy.
Zacznijmy od porównania obserwowanych wartości cechy \(y\), czyli \(y_i,i=1,2,\dots,n\), z wartościami teoretycznymi \(\hat{a}x_i+\hat{b}\) otrzymanymi na podstawie modelu \eqref{model}, gdzie \(\hat{a}\) i \(\hat{b}\) są jakimiś oszacowaniami parametrów \(a\) i \(b\). Skoro chcemy, aby nasz model był jak najlepiej dopasowany, to wartości \(y_i\) i \(\hat{a}x_i+\hat{b}\) powinny jak najmniej różnić się od siebie. Zatem różnice postaci \(y_i-(\hat{a}x_i+\hat{b})=y_i-\hat{a}x_i-\hat{b}\) powinny być jak najbliższe zeru. Różnice te nazywa się resztami. Jeśli \(\hat{a}\) i \(\hat{b}\) leżą blisko prawdziwych wartości \(a\) i \(b\) spodziewamy się, że sumarycznie wszystkie reszty będą możliwie małe.
Jednak reszty mogą być dodatnie lub ujemne (rzadziej zerem), więc prosta suma wszystkich reszt może być równa \(0\) nawet jeśli poszczególne reszty nie są bliskie zeru. Możemy więc zamiast reszt rozpatrywać kwadraty reszt, które mają tę zaletę że są zawsze nieujemne. Co więcej, reszty \(y_i-\hat{a}x_i-\hat{b}\) coraz bliższe zeru sprawiają, że kwadraty \((y_i-\hat{a}x_i-\hat{b})^2\) stają się coraz mniejsze i na odwrót.
Suma wszystkich kwadratów reszt będzie niewielka, gdy tylko każdy z kwadratów będzie niewielki. W wyborze estymatorów \(\hat{a}\) i \(\hat{b}\) będziemy więc starać się minimalizować sumę kwadratów reszt
\begin{equation}\label{sumakwreszt}
(y_1-\hat{a}x_1-\hat{b})^2+(y_2-\hat{a}x_2-\hat{b})^2+\dots+(y_n-\hat{a}x_n-\hat{b})^2.
\end{equation}
Oszacowania \(\hat{a}\) i \(\hat{b}\) parametrów \(a\) i \(b\) otrzymane poprzez minimalizację tej sumy nazywa się estymatorami metody najmniejszych kwadratów. Jest to najbardziej znana i najczęściej stosowana metoda szacowania parametrów regresji4. W pewnym sensie suma kwadratów reszt to jedna liczba, która pozwala nam wskazać prostą przybliżającą najlepiej nasze dane − dla każdej prostej wystarczy policzyć tę sumę, a następnie porównać otrzymane wyniki. Mniejszy wynik oznacza lepiej dopasowaną prostą.
Przykłady
Zanim przejdziemy do liczenia estymatorów metody najmniejszych kwadratów dla parametrów \(a\) i \(b\), zilustrujemy powyższe rozważania na przykładach korzystając z danych dotyczących dochodów i wydatków. Mianowicie spróbujemy wziąć trzy proste przechodzące przez dwa wybrane punkty (dla każdej prostej inne) spośród dziesięciu podanych w powyższej tabeli i wyznaczymy dla nich sumy kwadratów reszt. Przykładowo wybieramy następujące trzy pary punktów:
| pary punktów | prosta | współczynniki | suma reszt\(^2\) |
|---|---|---|---|
| \((210,140)\) i \((270,190)\) | \(y=\frac{5}{6}x-35\) | \(\hat{a}=\frac{5}{6}\) i \(\hat{b}=-35\) | \(5463,889\) |
| \((370,290)\) i \((400,310)\) | \(y=\frac{2}{3}x+43\frac{1}{3}\) | \(\hat{a}=\frac{2}{3}\) i \(\hat{b}=43\frac{1}{3}\) | \(4933,333\) |
| \((480,360)\) i \((520,390)\) | \(y=\frac{3}{4}x\) | \(\hat{a}=\frac{3}{4}\) i \(\hat{b}=0\) | \(4593,75\) |
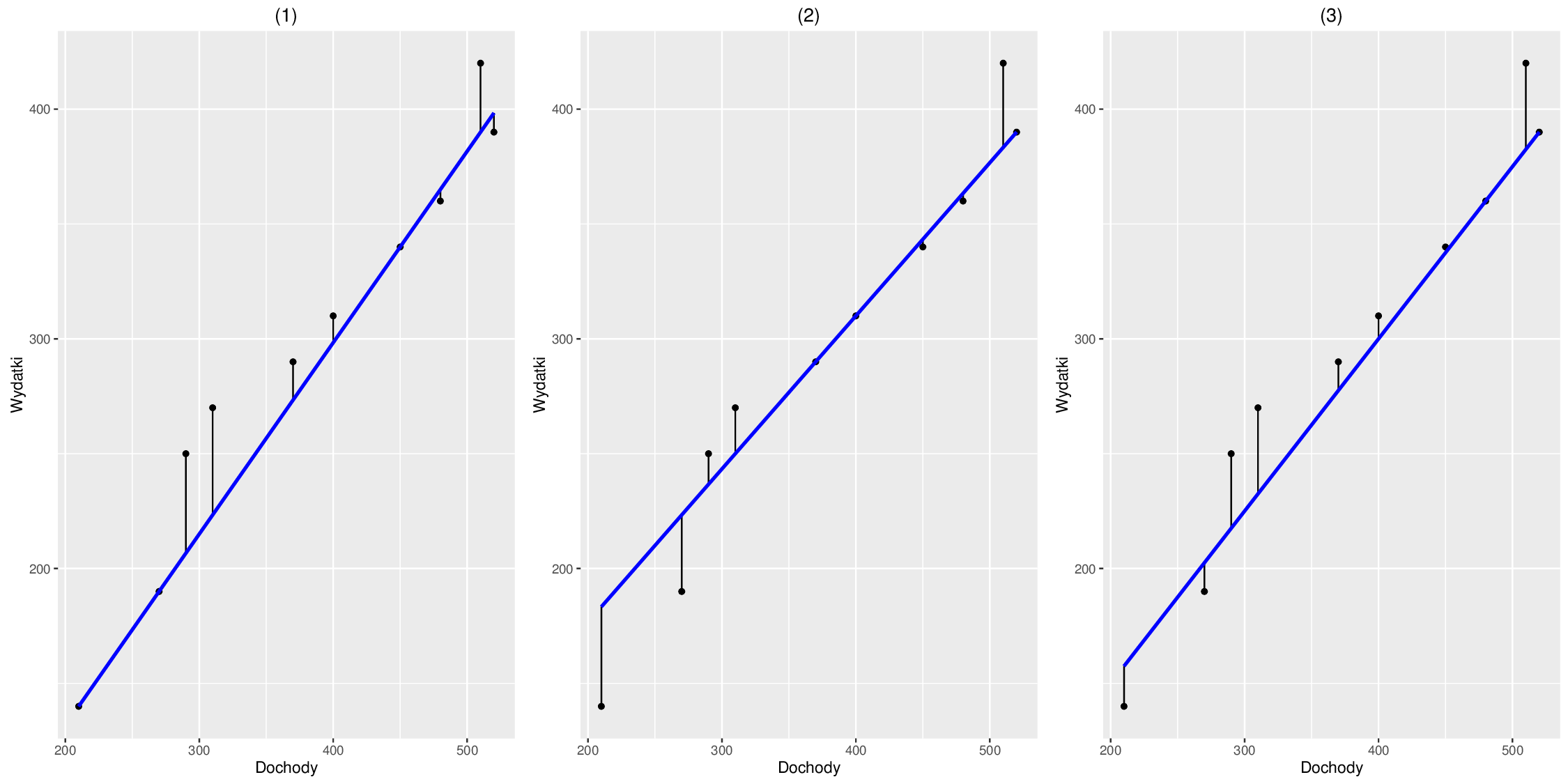
Wykres rozrzutu danych dotyczących miesięcznych dochodów i wydatków konsumpcyjnych w rodzinie w przeliczeniu na jedną osobę wraz z prostymi \(y=\frac{5}{6}x-35\) (1), \(y=\frac{2}{3}x+43\frac{1}{3}\) (2), \(y=\frac{3}{4}x\) (3) oraz odcinkami reprezentującymi reszty
Na powyższym rysunku proste zostały naniesione na wykres rozrzutu. Dodatkowo kolorem czarnym narysowane zostały odcinki łączące punkty \((x_i,y_i)\) podane w tabeli 1 i ich odpowiedniki \((x_i,\hat{a}x_i+\hat{b})\) wynikające z przyjętej prostej jako modelu. Oczywiście tam, gdzie dany punkt z tabeli 1 leży na prostej, odcinek pionowy ma długość \(0\). Tak jak się spodziewaliśmy żadna prosta nie przechodzi przez wszystkie punkty odpowiadające obserwacjom. Zatem, aby określić, która z nich jest najlepiej dopasowana do danych, obliczymy sumy kwadratów reszt \eqref{sumakwreszt} dla każdej z osobna. Przykładowo dla pierwszej prostej mamy:
\begin{align*}
&\left(y_1-\frac{5}{6}x_1+35\right)^2+\left(y_2-\frac{5}{6}x_2+35\right)^2+\dots+\left(y_{10}-\frac{5}{6}x_{10}+35\right)^2\\
&=\left(140-\frac{5}{6}\cdot 210+35\right)^2+\left(190-\frac{5}{6}\cdot 270+35\right)^2+\dots+\left(390-\frac{5}{6}\cdot 520+35\right)^2\\
&=5463{,}889.
\end{align*}
Analogicznie dla drugiej i trzeciej prostej uzyskujemy \(4933{,}333\) i \(4593{,}75\), odpowiednio. Zatem wśród wybranych trzech prostych, ostatnia z nich opisana równaniem \(y=\frac{3}{4}x\) jest najlepiej dopasowana do danych dotyczących dochodów i wydatków w sensie sumy kwadratów reszt \eqref{sumakwreszt}. Jak zobaczymy za chwilę nawet ona jest o wiele gorsza od najlepszej prostej \(y=\hat{a}x+\hat{b}\), gdzie \(\hat{a}\) i \(\hat{b}\) są estymatorami metody najmniejszych kwadratów minimalizującymi tę sumę.
Zaczęcamy czytelnika do eksperymetowania − na poniższym wykresie można modyfikować wartości \(a\) i \(b\) i próbować dopasować te wartości tak, by w najlepszy sposób dopasować do danych w tabeli 1. Następnie, otrzymane wyniki można porównać z optymalnym rozwiązaniem zaprezentowanym poniżej.
Prosta regresji
Oszacowania parametrów \(a\) i \(b\) uzyskane metodą najmniejszych kwadratów mają postać5
\begin{equation}\label{estymatory}
\hat{a}=
\frac{y_1(x_1-\bar{x})+y_2(x_2-\bar{x})+\dots+y_n(x_n-\bar{x})}
{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\dots+(x_n-\bar{x})^2},\quad
\hat{b} =\bar{y}-\bar{x}\hat{a},
\end{equation}
gdzie \(\bar{x}=\frac{1}{n}(x_1+x_2+\dots+x_n)\) i \(\bar{y}=\frac{1}{n}(y_1+y_2+\dots+y_n)\) są średnimi arytmetycznymi z obserwacji zmiennych \(x\) i \(y\), odpowiednio. Otrzymujemy zatem prostą postaci \(y=\hat{a}x+\hat{b}\) zwaną prostą regresji opisującą zależność między zmiennymi \(x\) i \(y\). Współczynnik kierunkowy \(\hat{a}\) nazywamy współczynnikiem regresji liniowej.
Policzmy więc wartości estymatorów metody najmniejszych kwadratów oraz prostą regresji dla danych dotyczących dochodów i wydatków. Zaczynamy od obliczenia średnich arytmetycznych dla obu zmiennych:
\begin{align*}
\bar{x}=&\frac{x_1+x_2+\dots+x_{10}}{10}=\frac{210+270+\dots+520}{10}=381,\\
\bar{y}=&\frac{y_1+y_2+\dots+y_{10}}{10}=\frac{140+190+\dots+390}{10}=296.
\end{align*}
Aby obliczyć wartość estymatora \(\hat{a}\) wykonamy obliczenia pomocnicze podane w poniższej tabeli.
| \(i\) | \(x_i\) | \(y_i\) | \(x_i-\bar{x}\) | \(y_i(x_i-\bar{x})\) | \((x_i-\bar{x})^2\) |
|---|---|---|---|---|---|
| \(1\) | \(210\) | \(140\) | \(-171\) | \(-23940\) | \(29241\) |
| \(2\) | \(270\) | \(190\) | \(-111\) | \(-21090\) | \(12321\) |
| \(3\) | \(290\) | \(250\) | \(-91\) | \(-22750\) | \(8281 \) |
| \(4\) | \(310\) | \(270\) | \(-71\) | \(-19170\) | \(5041 \) |
| \(5\) | \(370\) | \(290\) | \(-11\) | \(-3190\) | \(121 \) |
| \(6\) | \(400\) | \(310\) | \(19\) | \(5890\) | \(361 \) |
| \(7\) | \(450\) | \(340\) | \(69\) | \(23460\) | \(4761 \) |
| \(8\) | \(480\) | \(360\) | \(99\) | \(35640\) | \(9801 \) |
| \(9\) | \(510\) | \(420\) | \(129\) | \(54180\) | \(16641 \) |
| \(10\) | \(520\) | \(390\) | \(139\) | \(54210\) | \(19321 \) |
| Suma: | \(83240\) | \(105890\) |
Korzystając z niej oraz ze wzorów \eqref{estymatory} otrzymujemy
\[
\hat{a}=\frac{83240}{105890}\simeq
0{,}7860988,\quad\hat{b}=296-381\cdot 0{,}7860988\simeq -3{,}503636,
\]
zatem prosta regresji ma postać \(y=0{,}7860988x-3{,}503636\).
Na poniższym rysunku prosta regresji została naniesiona na wykres rozrzutu. Jak widzimy całkiem przyzwoicie jest ona dopasowana do obserwacji. Suma kwadratów reszt dana wzorem \eqref{sumakwreszt} dla powyższych wartości estymatorów metody najmniejszych kwadratów wynosi \(3405{,}137\). Jest ona znacznie mniejsza od sum dla trzech przykładowych prostych rozważanych powyżej.
Tak jak już wcześniej zauważyliśmy zazwyczaj wzrostowi dochodów odpowiada wzrost wydatków, co jest tutaj potwierdzone dodatnim współczynnikiem regresji liniowej \(\hat{a}=0{,}7860988\).
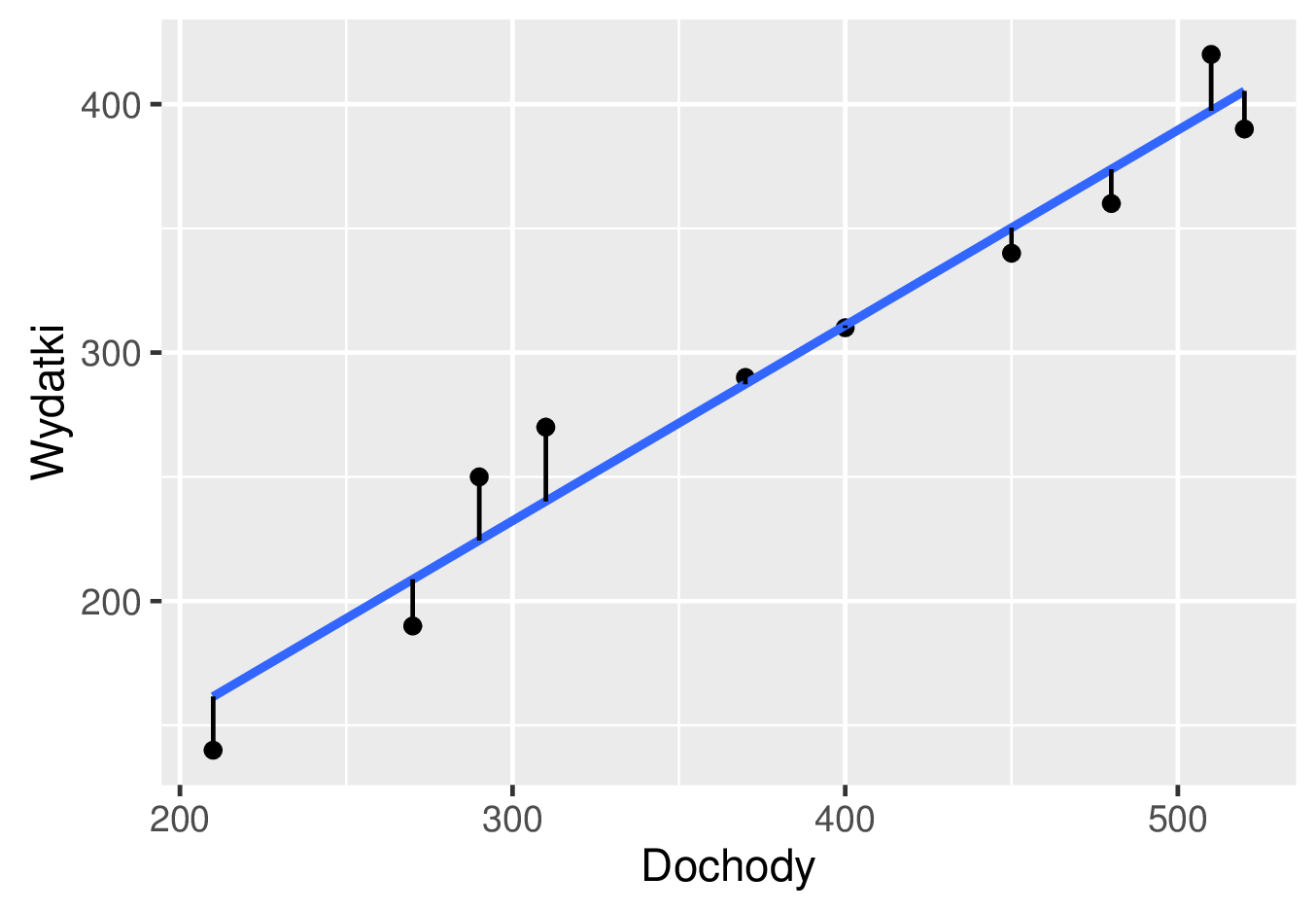
Wykres rozrzutu danych dotyczących miesięcznych dochodów i wydatków konsumpcyjnych w rodzinie w przeliczeniu na jedną osobę wraz z dopasowaną prostą regresji \(y=0{,}7860988x-3{,}503636\) oraz odcinkami reprezentującymi reszty
Predykcja
Do tej pory opisaliśmy model regresji liniowej, a ponadto oszacowaliśmy jego parametry, czyli współczynnik kierunkowy \(a\) i wyraz wolny \(b\). Zatem funkcja liniowa \(y=\hat{a}x+\hat{b}\) opisuje przybliżoną zależność między zmiennymi \(x\) i \(y\). Poniżej przedstawimy główne zastosowanie tego opisu.
Problem, który chcemy rozwiązać za pomocą regresji liniowej, opiszemy na bazie danych dotyczących dochodów i wydatków. Tabela 1 podaje wartości dochodów i wydatków dla dziesięciu rodzin. Załóżmy, że dochody jedenastej rodziny wynoszą 350 złotych, ale nie znamy wartości wydatków w tej rodzinie. Przypuśćmy, że z jakiś przyczyn chcielibyśmy przewidzieć te wydatki. Zauważmy, że tabela 1 nie zawiera obserwacji, dla której dochody wynoszą 350 złotych, tj. \(x=350\), więc nie możemy z niej bezpośrednio skorzystać. Taki problem przewidywania możliwej wartości zmiennej \(y\) (wydatki) dla nowej wartości (\(x_{\text{nowy}}=350\)) zmiennej \(x\) (dochody), która jest różna od każdej obserwacji tej zmiennej (\(x_{\text{nowy}}\notin\{x_1,x_2,\dots,x_n\}\)) nosi nazwę predykcji. Predykcja jest ważnym zagadnieniem statystyki matematycznej o szerokich zastosowaniach.
W jaki sposób dokonać takiego przewidywania, czyli predykcji? Przypomnijmy, że wyznaczając prostą regresji \(y=\hat{a}x+\hat{b}\) staraliśmy się, aby wartości \(\hat{a}x_i+\hat{b}\) jak najlepiej (w sensie sumy kwadratów reszt \eqref{sumakwreszt}) przybliżały obserwacje \(y_i\), tj. \(y_i\approx\hat{a}x_i+\hat{b}\). Dzięki temu obserwacje \(y_i\) możemy przybliżyć (niejako zastąpić) wartościami \(\hat{a}x_i+\hat{b}\). Tę ideę można wykorzystać do predykcji w oparciu o model regresji liniowej. Mianowicie, przybliżenia (przewidywania, predykcji) zmiennej \(y\) dla nowej wartości \(x_{\text{nowy}}\) zmiennej \(x\) dokonujemy według wzoru
\begin{equation}\label{predykcja}
\hat{a}x_{\text{nowy}}+\hat{b},
\end{equation}
czyli wystarczy podstawić wartość \(x_{\text{nowy}}\) zmiennej \(x\) do naszej prostej regresji \(y=\hat{a}x+\hat{b}\). Oczywiście punkt \((x_{\text{nowy}},\hat{a}x_{\text{nowy}}+\hat{b})\) leży na tej prostej (patrz poniższy rysunek).
Dla ilustracji przeprowadźmy predykcję wartości wydatków w jedenastej rodzinie z dochodem równym \(x_{\text{nowy}}=350\) złotych. Wyprowadzona w poprzednim punkcie prosta regresji ma postać \(y=0{,}7860988x-3{,}503636\). Zgodnie ze wzorem \eqref{predykcja} uzyskujemy
\[
0{,}7860988\cdot 350-3{,}503636=271{,}6309.
\]
Zatem dla rodziny o dochodzie w przeliczeniu na jedną osobę równym \(350\) złotych możemy spodziewać się wydatków w przeliczeniu na jedną osobę równych około \(272\) złote.
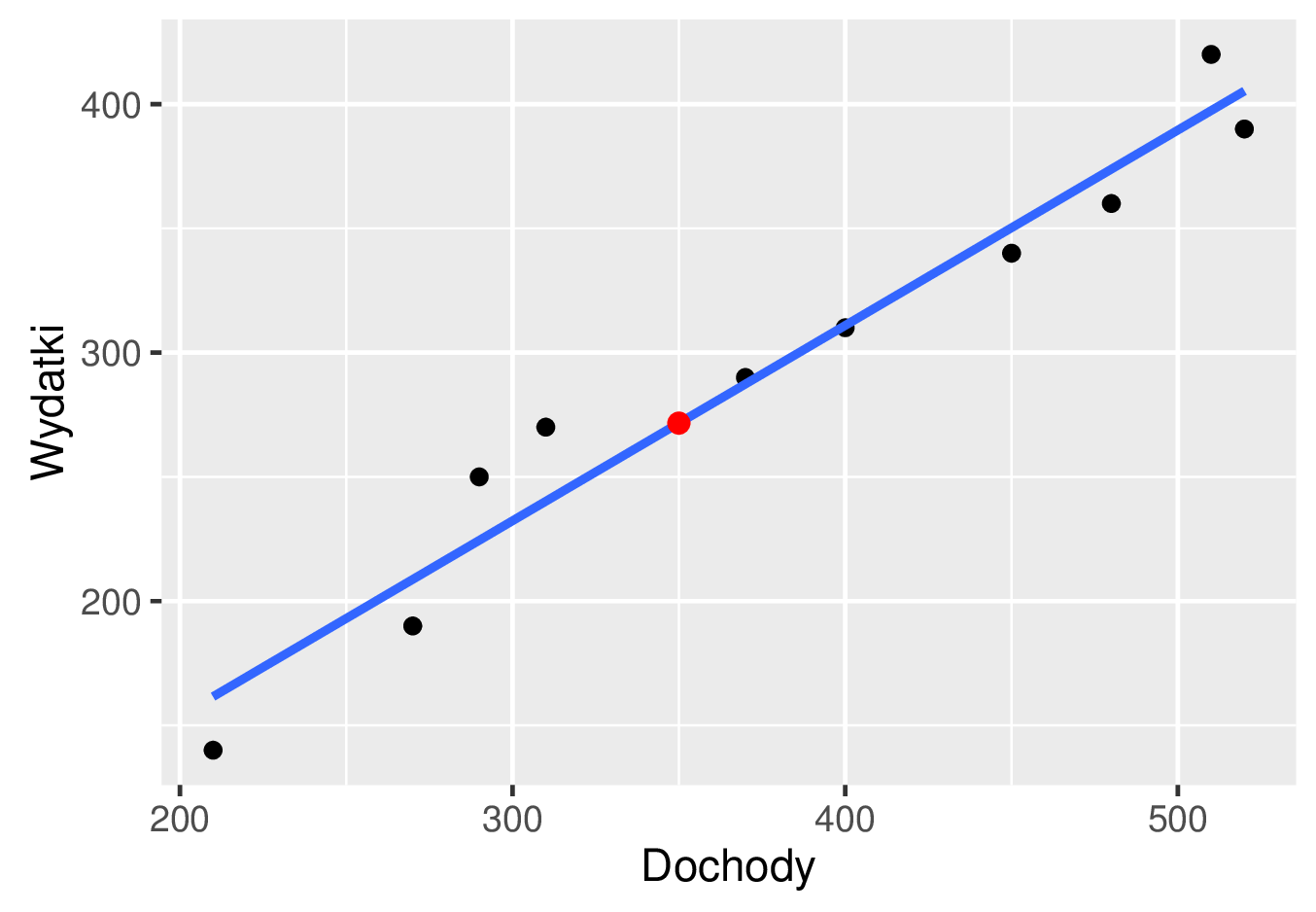
Wykres rozrzutu danych dotyczących miesięcznych dochodów i wydatków konsumpcyjnych w rodzinie w przeliczeniu na jedną osobę wraz z dopasowaną prostą regresji \(y=0{,}7860988x-3{,}503636\) oraz punktem (zaznaczonym kolorem czerwonym) reprezentującym predykcję wydatków w rodzinie o dochodzie równym \(350\) złotych.
Obliczenia przedstawione w niniejszym artykule można (a nawet należy!) wykonać również za pomocą programów komputerowych przeznaczonych specjalnie do tego celu. Przykładowym takim programem jest R, który cieszy się coraz większą popularnością wśród osób zajmujących się statystyką matematyczną i jej zastosowaniami. Więcej informacji o nim, jak i o rozważanej tu regresji liniowej można znaleźć w podanej poniżej literaturze.
Podziękowania
Applet w Geogebrze przygotowali Kajetan Strzyżewski i Krzesimir Małecki z klasy 2B MKA z VIII Liceum Ogólnokształcącego w Poznaniu.
Bibliografia
- Biecek P. (2008). Przewodnik po pakiecie R. GIS.
- Biecek P. (2011). Analiza danych z programem R. Modele liniowe z efektami stałymi, losowymi i mieszanymi. Wydawnictwo Naukowe PWN.
- Górecki T. (2011). Podstawy statystyki z przykładami w R. BTC.
- Krzyśko M. (2000). Wielowymiarowa analiza statystyczna. Wydawnictwo Naukowe UAM.
Przypisy
- A w zasadzie jest praktycznie niemożliwy.
- Można to uzasadnić w następujący sposób: ponieważ gospodarstwa domowe nie mogą (na dłuższą metę) wydawać więcej niż zarabiają, kwota przeznaczana na wydatki konsumpcyjne to kwota dochodów pomniejszona o podatki (i opcjonalnie: comiesięczne oszczędności). Ponieważ obciążenie podatkowe rośnie liniowo (w ramach jednej stawki) podobnie muszą więc zachowywać się wydatki konsumpcyjne. Ewentualna stała może pochodzić od dywidend i bezpośredniej (lub pośredniej) pomocy państwa.
- Często w modelu regresji liniowej uwzględnia się dodatkowe składniki \(e_i\) opisujące błędy przypadkowe. Wtedy model jest zadany wzorem postaci \(y_i=ax_i+b+e_i\). O składnikach \(e_i\) często zakłada się że mają specyficzny rozkład (np. normalny), jednak jest to temat wykraczający poza ramy niniejszego artykułu.
- Do każdej z reszt można zaaplikować dowolną inną ciągłą funkcję, która jest dodatnia i zbiega do \(0\) tylko gdy reszta jest bliska \(0\). Jedną taką funkcję już znamy − jest to funkcja kwadratowa. Jaką inną mógłbyś zaproponować?
- Wyprowadzenia tychże wzorów znajdą się w następnym artykule
Artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''. Zobacz następną część tego artykułu
