Magicy i iluzjoniści od wielu już lat wprawiają w zachwyt spragnionych wrażeń ludzi. Sztuczki karciane, upowszechnione przez Davida Copperfielda, należą do najczęściej wykorzystywanych przez nich metod zabawiania publiczności. Jak się okazuje, nie trzeba posiadać szczególnych umiejętności magicznych, aby móc zadziwiać talią kart — wystarczy odrobina matematyki.
Magia!
Wyobraźcie sobie, że jesteście na pokazie znanego iluzjonisty. W trakcie występu magik wyjmuje z kieszeni talię 32 kart i pyta o pięciu ochotników. Następnie podchodzi do losowej osoby z tłumu i prosi ją o przełożenie talii (czyli zabranie jej wierzchniej części i położenie obok). Podchodzi teraz do każdej z chętnych osób i podaje im po jednej z pięciu kolejnych kart ze stosu. Prosi przy tym, aby dokładnie przyjrzeli się otrzymanej karcie, nie pokazując jej nikomu innemu. Zwraca się do ochotników słowami:
— Proszę was teraz, byście użyli swoich zdolności telepatycznych i przesłali mi obraz waszych kart.
Na twarzach uczestników widać skupienie, gdy starają się wykonać polecenie iluzjonisty. Po chwili ten jednak mówi:
— Obawiam się, że dostaję zbyt dużo informacji od was w jednym czasie. Czy ci, którzy mają czerwone karty mogą wstać na chwilę i spróbować telepatii jeszcze raz?
W tym momencie z krzeseł podnoszą się dwie pierwsze osoby. Nie mija kilka sekund, a magik oznajmia, że pierwsza z nich dzierży asa kier, a druga dwójkę karo. Następnie zwraca się do pozostałej trójki ochotników i poprawnie nazywa trzymane przez nich czarne karty. Powyższy pokaz nie wymaga podstawionych statystów, znaczonych kart, ani magicznych zdolności. Na czym więc polega ta sztuczka? Poznajmy matematykę, która się za nią kryje!
Ciągi de Bruijna
Część z was pewnie już się domyśliła, że kluczowe znaczenie ma to, że karty są ułożone w ustalonej kolejności. Nie wyjaśnia to jednak zagadki, w jaki sposób iluzjonista jest w stanie nazwać pięć kart jedynie na podstawie informacji o ich kolorach. Aby ją rozwiązać musimy poznać pewne ,,magiczne” obiekty, a mianowicie ciągi de Bruijna.
Ciągiem de Bruijna rzędu n nazywamy cykliczny, binarny ciąg, w którym każdy binarny podciąg (lub inaczej: podsłowo) długości n występuje dokładnie raz. Będziemy oznaczać go jako B(n) 1.
Definicja na pierwszy rzut oka wydaje się być skomplikowana. Wyjaśnijmy więc pojęcia w niej użyte. Przez ciągi binarne rozumiemy takie ciągi, w których występować mogą jedynie dwa symbole, w naszym przypadku: 0 i 1. Podsłowem długości n nazywamy podciąg złożony z n kolejnych elementów danego ciągu. Czym z kolei jest ciąg cykliczny? Najprościej będzie wyobrazić sobie zapisanie jego elementów na okręgu, jak na poniższym rysunku:
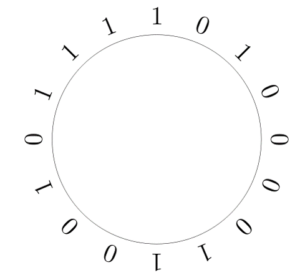
Ciąg cykliczny 1010000110010111
Zobaczmy jak poznana teoria prezentuje się na przykładzie:
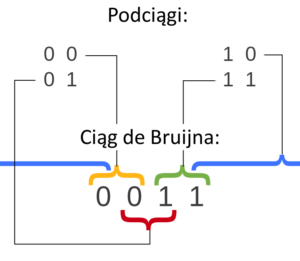
Graficzna interpretacja ciągu B(2)
Wszystkie możliwe binarne podsłowa długości 2 tego ciągu to: 00, 01, 10 i 11. Jak łatwo zauważyć na Rysunku powyżej, każdy z nich występuje w B(2) dokładnie raz. Analogicznie dla ciągu B(3), który jest postaci 01000111 — wszystkie podciągi binarne długości 3 to: 010, 100, 000, 001, 011, 111, 110, 101. Każdy z nich występuje w B(3) dokładnie jeden raz.
Pewnie zadajecie sobie właśnie pytanie co mają te dziwne ciągi wspólnego z opisaną sztuczką. Już spieszę z wyjaśnieniami! Wiemy, że w ciągu B(3) wszystkie ciągi długości 3, które można utworzyć ze znaków zbioru {0,1} występują dokładnie jeden raz. To znaczy, że na przykład sekwencja 110 nie powtórzy się kilka razy w tym ciągu de Bruijna. A co gdyby był to ciąg, w którym każdy pięcioelementowy podciąg, np. 11000, występuje dokładnie raz? Brzmi znajomo?
Matematyka!
Prawdziwi magicy nie zdradzają swoich sztuczek. Na szczęście nie jestem żadnym iluzjonistą, a matematykiem, więc uchylę przed wami rąbka tajemnicy. W tej karcianej sztuczce znalazł zastosowanie ciąg B(5). Wygląda on tak:
00001001011001111100011011101010.
Istnieje prosty sposób na wygenerowanie tego ciągu. Zanim jednak go przedstawię należy wyjaśnić, czym jest dodawanie modulo2. W naszym przypadku działanie to sprowadza się do czterech równości:
0+0=0,0+1=1,1+0=1,1+1=0,
które łatwo jest sobie przyswoić: wystarczy zapamiętać, że gdy suma jest parzysta zapisujemy 0, w przeciwnym przypadku: 1.
Wracając do ciągu B(5): zaczynamy od 00001, a kolejną cyfrę obliczamy dodając do siebie pierwszą i trzecią modulo 2: 0+0, otrzymując 0. Dopisujemy wynik na koniec ciągu, otrzymując 000010. Następnie przesuwamy się w prawo, czyli zapominamy o cyfrze na początku i powtarzamy ten krok (tym razem rozpatrując ciąg 00010). Podobnie jak poprzednio, dodajemy cyfry na pierwszej i trzeciej pozycji: (0+0)mod2=0, a następnie dopisujemy to 0 na koniec ciągu. Po tym kroku ma on postać 0000100. Przesuwamy się w prawo raz jeszcze (więc pomijamy teraz dwie pierwsze cyfry), rozważamy więc ciąg 00100. Tym razem, obliczając sumę modulo 2 pierwszej i trzeciej cyfry otrzymamy 1. Po dopisaniu tej cyfry na koniec ciągu otrzymujemy 00001001. Postępując dalej w ten sposób, otrzymamy wspomniany wcześniej binarny ciąg de Bruijna rzędu 53.
Aby jednak ciąg ten mógł nam się do czegoś przydać, musimy poznać sposób, w jaki można go powiązać z 32-elementową talią: otóż każdy jego 5 elementowy podciąg będzie odpowiadał jednej karcie.
Każda zakodowana karta przyjmuje postać abcde. Pierwsze dwa znaki odpowiadają za kolor, kolejne trzy — za figurę. Przy określaniu koloru wyróżniamy barwę (czerwony zapisujemy jako 1, natomiast czarny — jako 0) oraz starszeństwo: przyjmijmy (zgodnie ze znaną grą karcianą), że kiery (♥) są starsze od kar (♦), zaś piki (♠) są starsze od trefli (♣). W ten sposób otrzymujemy:
| 11 — ♥ | 10 — ♦ | 01 — ♠ | 00 — ♣ |
Kodowanie figur wygląda następująco:
| 000 | As |
| 001 | 2 |
| 010 | 3 |
| 011 | 4 |
| 100 | 5 |
| 101 | 6 |
| 110 | 7 |
| 111 | 8 |
Oczywiście nikt nie chciałby uczyć się tego na pamięć! Istnieje prosty sposób, aby rozpoznać, jaka figura kryje się za danym ciągiem cyfr. W życiu codziennym posługujemy się system dziesiętnym. Zapis 324 oznacza liczbę, którą możemy zapisać jako 324=3⋅102+2⋅101+4⋅100.
(110)2=1⋅22+1⋅21+0⋅20=4+2=6.
Aby więc uzyskać informację o tym, jaką figurę karcianą reprezentuje dany ciąg w naszym przykładzie, zamieniamy liczbę dwójkową na system dziesiętny i dodajemy jeden.
Jeśli wszystkie podciągi długości 5 ciągu B(5) zakodujemy zgodnie z powyższymi wytycznymi otrzymamy następujące ułożenie talii kart:
♣2, ♣3, ♣5, ♠2, ♦3, ♣6, ♠4, ♦7, ♠5, ♥ 2, ♦4, ♣8, ♠8, ♥8, ♥7, ♥5, ♥A, ♦2, ♣4, ♣7, ♠6, ♥4, ♦8, ♠7, ♥6, ♥3, ♦6, ♠3, ♦5, ♠A, ♦A, ♣A.
A czy te ciągi przydają się jeszcze do czegoś?
Iluzjonistyczne triki to nie jedyna dziedzina, w której ciągi de Bruijna znalazły zastosowanie. Pewna istotna własność tych ciągów, a mianowicie to, że żaden podciąg nie występuje w nim więcej niż raz, sprawiła, że były one niezwykle przydatne w rozwoju kryptologii. Zauważmy, że każdy k-elementowy podciąg może odpowiadać innemu znakowi zakodowanej wiadomości! Czyż nie stwarza to ogromnych możliwości w szyfrowaniu tekstów?
Możemy również wyróżnić macierze de Bruijna. Są one uogólnieniem ciągów na dwa wymiary i znalazły zastosowanie w widzeniu komputerowym. Wyobraźcie sobie robota przemysłowego, który porusza się po długim korytarzu w jedną i w drugą stronę. Chcielibyśmy jednak, aby robot potrafił dokładnie określić gdzie się znajduje. Pewien matematyk zauważył, że pole pod urządzeniem można traktować jako macierz de Bruijna. Dzięki temu, że każda podmacierz występuje w niej wyłącznie jeden raz, robot potrafi jednoznacznie określić, na którym polu się znajduje. Na tej samej zasadzie działa długopis cyfrowy wprowadzony na rynek przez firmę Anoto. Aby móc się nim posługiwać potrzebna jest kartka zadrukowana kropkami, które w rzeczywistości tworzą macierz de Bruijna. Podobnie jak poprzednio, kamera umieszczona w długopisie sczytuje okno macierzy, w którym się znajduje i na tej podstawie jest w stanie określić swoją lokalizację na danej stronie.
Oprócz powyższych zastosowań, obiekty de Bruijna, ze względu na swoje wyjątkowe własności, są również przedmiotem wielu badań teoretycznych.
Sekret sztuczki wyjawiony!
Skoro już wiemy na czym polega cała magia, jeszcze raz przeanalizujmy naszą sztuczkę. Przypomnijmy sytuację ze wstępu: mamy 5 ochotników, pierwszych dwoje ma karty czerwone, pozostali czarne. Czerwony zapisywać będziemy jako 1, czarny natomiast jako 0. Otrzymujemy więc ciąg 11000. Ciąg ten odpowiada karcie, którą posiada pierwsza osoba — 11 oznacza, że jest to kier, natomiast po zamianie liczby 000 na system dziesiętny i dodaniu jedynki dowiadujemy się, że jest to as. Karta pierwszej osoby to ♥A. Aby dowiedzieć się jaka jest druga karta, dodajemy pierwszą i trzecią cyfrę ciągu modulo 2 (1+0=1), przesuwamy ciąg o jedno miejsce w prawo (zapominamy więc o pierwszym znaku) i dopisujemy wynik wcześniejszego dodawania. Nasz ciąg jest teraz postaci 10001. 10 to karo, natomiast 001 oznacza dwójkę. Zatem drugi ochotnik dzierży więc w dłoni ♦2. Postępując dalej w ten sam sposób dowiemy się, że pozostałe trzy karty to: ♣4, ♣7 oraz ♠6.
Spróbujcie tego w domu i zachwyćcie swoich znajomych!
Przypisy
- Jest to pewne uproszczenie idei ciągów de Bruijna. W większej ogólności rozważa się ciągi złożone nie tylko z 0 i 1. Mówi się wtedy o ciągach B(k,n), gdzie k jest liczbą różnych symboli dopuszczalnych w ciągu. Ciągi B(n), o których wspominamy w artykule można wówczas interpretować jako B(2,n)
- W ogólnym przypadku wynikiem dodawania modulo m dwóch liczb jest reszta z dzielenia ich sumy przez m, np. 4+3=2 (mod5)
- Przedstawiony algorytm generuje poprawny ciąg de Bruijna dla n=5, o czym można się przekonać bezpośrednim sprawdzeniem (własnoręcznie, lub pisząc odpowiedni program znajdujący wszystkie podciągi długości 5). Chcielibyśmy wiedzieć, że ten algorytm daje poprawny ciąg dla wszystkich n, ale dowód tego stwierdzenia nie jest znany. Istnieją natomiast inne sposoby generowania ciągów de Bruijna
Artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.
