Blaise Pascal znany również jako Błażej Pascal był jednym z najsłynniejszych matematyków francuskich XVII wieku. W wieku zaledwie 16 lat podał twierdzenie, które jest jednym z jego najsłynniejszych! Prezentujemy je poniżej i zachęcamy młodych czytelników do samodzielnego zmierzenia się z dowodem. W razie niepowodzenia zachęcamy do przeczytania dowodu w podręczniku „Geometria analityczna w n-wymiarach” Karola Borsuka, słynnego polskiego geometry i topologa XX wieku. Dowód znajduje się na stronie 272 części II .
Twierdzenie (Blaise Pascal):
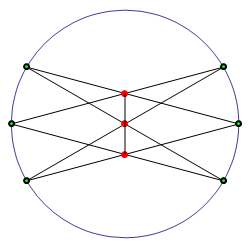
Trzy punkty przecięcia par boków przeciwległych sześciokąta wpisanego w stożkową leżą na jednej prostej (tzw. prosta Pascala).
W poniższym module interaktywnym prezentujemy wersję twierdzenia, w której stożkowa może być elipsą, parą prostych lub hiperbolą. Parametr a kontroluje promień krzywej, natomiast parametr r współczynnik przy zmiennej y. Na ekranie można poruszać sześcioma punktami z zielonym wnętrzem umieszczając je w różnych miejscach na krzywej. Prosta Pascala jest wyznaczona przez trzy czerwone punkty przecięcia.
