Ciągłość funkcji jest jednym z najważniejszych pojęć w analizie matematycznej. Jej definicja nie jest banalna i wymaga pewnego przyzwyczajenia. Zawiera aż trzy kwantyfikatory, dwa przedziały o różnych długościach, implikację logiczną, jeden argument funkcji stały i jeden zmienny, greckie litery ($\epsilon$ czytamy: „epsilon”, $\delta$ czytamy: „delta”)… Zdecydowanie trzeba się mocno w tę definicję wmyślić, by potem używać jej ze swobodą. Pomocne mogą okazać się przykłady: zarówno funkcji ciągłych, jak i funkcji w pewnych punktach nieciągłych, w szczególności funkcji nieciągłych w „bardzo wielu” punktach.

Ciągłość i nieciągłość

Definicja 1. Funkcję $f$ określoną na zbiorze liczb rzeczywistych i o wartościach w zbiorze liczb rzeczywistych nazywamy ciągłą w punkcie $x_0$, gdy dla każdej dodatniej liczby $\epsilon$ istnieje dodatnia liczba $\delta$ taka, że jeżeli $|x-x_0|<\delta$, to $|f(x)-f(x_0)|<\epsilon$.

Definicja 2. Funkcję $f$ określoną na zbiorze liczb rzeczywistych i o wartościach w zbiorze liczb rzeczywistych nazywamy ciągłą, gdy jest ona ciągła w każdym punkcie swojej dziedziny.

O funkcji, która nie jest ciągła w punkcie $x_0$, mówimy, że jest funkcją nieciągłą w punkcie $x_0$. Punkt, w którym funkcja jest ciągła, nazywamy punktem ciągłości funkcji, a punkt, w którym funkcja nie jest ciągła – jej punktem nieciągłości.

Jeżeli chcemy pokazać, że funkcja $f$ jest ciągła w pewnym punkcie $x_0$, dla każdej dodatniej liczby $\epsilon$ musimy przeprowadzić test, który polega na tym, by znaleźć taką dodatnią liczbę $\delta$ – być może bardzo małą – że nierówność $|x-x_0|<\delta$ pociąga za sobą nierówność $|f(x)-f(x_0)|<\epsilon$. Jeżeli choćby dla jednej liczby $\epsilon$, nie uda nam się znaleźć takiej liczby $\delta$, by powyższy warunek był spełniony, to znaczy, że funkcja $f$ nie jest ciągła w punkcie $x_0$.

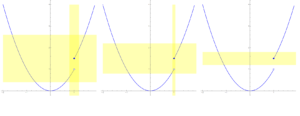
Proces testowania możemy zilustrować graficznie. Wybór dodatniej liczby $\epsilon$ wyznacza nieskończenie długi poziomy pasek o szerokości $2\epsilon$ wokół linii $y=f(x_0)$. Dobranie dodatniej liczby $\delta$ pozwala narysować nieskończenie długi pionowy pasek o szerokości $2\delta$ wokół linii $x=x_0$. Przecinające się paski wyznaczają prostokąt. Pozytywna odpowiedź liczby $\delta$ na wyzwanie reprezentowane przez zadaną liczbę $\epsilon$ oznacza, że ta część wykresu funkcji, która znajduje się w pionowym pasku, zarazem mieści się w poziomym pasku, czyli dokładnie w prostokącie powstałym z przecięcia obu pasków, gdyż to właśnie mówi warunek: jeżeli $|x-x_0|<\delta$, to $|f(x)-f(x_0)|<\epsilon$. Jeżeli uda nam się pokazać, że zawsze istnieje pozytywna odpowiedź dodatniej liczby $\delta$ na wyzwanie reprezentowane przez dowolną dodatnią liczbę $\epsilon$, to będzie oznaczało, że funkcja $f$ jest ciągła w punkcie $x_0$. Ale jeżeli choć raz pozytywna odpowiedź będzie niemożliwa, będzie to wystarczający powód, aby uznać, że funkcja $f$ nie jest ciągła w punkcie $x_0$.

Na poniższej ilustracji pokazano wykres funkcji, która nie jest ciągła w punkcie $x_0=1$. Co prawda znalazła się pozytywna odpowiedź na wyzwanie reprezentowane przez $\epsilon=1,1$ w postaci liczby $\delta=0,2$, a także na wyzwanie reprezentowane przez $\epsilon=0,7$ w postaci liczby $\delta=0,06$, ale dla $\epsilon=0,3$ nie udaje się już znaleźć takiej liczby $\delta$, aby wykres funkcji leżący w pionowym pasku mieścił się jednocześnie w poziomym pasku, czyli aby nie wychodził poza prostokąt powstały z przecięcia obu pasków.

Podajemy jeszcze kilka wykresów innych funkcji, które nie są ciągłe w punkcie $x_0=1$.

Czytelnik na pewno sam łatwo wymyśli przykłady funkcji, które mają więcej niż jeden punkt nieciągłości: 2, 3, 10 lub nieskończenie wiele punktów nieciągłości. Poniżej zbadamy trzy przykłady funkcji określonych na prostej rzeczywistej, które są „bardzo nieciągłe”, tzn. które mają szczególnie wiele punktów nieciągłości.

Pierwsza funkcja jest nieciągła na całej swojej dziedzinie. Druga jest nieciągła dla argumentów wymiernych, a ciągła dla wszystkich argumentów niewymiernych. Trzecia funkcja ma takie same punkty ciągłości i nieciągłości jak druga, ale dodatkowo jest jeszcze rosnąca.

Ten krótki tekst zakończymy sformułowaniem pytania, które z pewnością narzuci się Czytelnikowi w toku dalszej lektury, i podamy zwięzłą, być może zaskakującą odpowiedź.

Funkcja Dirichleta

Funkcję Dirichleta definiujemy na zbiorze liczb rzeczywistych wzorem
$$f(x)= \begin{cases} 1 & \text{jeśli } x \text{ jest liczbą wymierną;}\\ 0 & \text{jeśli } x \text{ jest liczbą niewymierną.}\\ \end{cases}$$
Pokażemy, że każda liczba rzeczywista jest punktem nieciągłości funkcji Dirichleta.

Twierdzenie. Funkcja Dirichleta jest nieciągła dla wszystkich argumentów.

W dowodzie wykorzystany zostanie następujący fakt.

Fakt. Między dowolnymi dwiema różnymi liczbami rzeczywistymi można znaleźć co najmniej jedną liczbę wymierną i co najmniej jedną liczbę niewymierną.

(Tak naprawdę liczb wymiernych i liczb niewymiernych mieszczących się między dwiema różnymi liczbami rzeczywistymi jest zawsze znacznie więcej niż jedna!)

Dowód. Niech $x_0$ będzie dowolną liczbą rzeczywistą i niech $\epsilon=1/2$. Wówczas zgodnie z wyżej przytoczonym faktem dla każdej dodatniej liczby $\delta$ istnieje $x$ takie, że $|x-x_0|<\delta$ (jeżeli $x_0$ jest liczbą wymierną, $x$ będzie liczbą niewymierną, a jeżeli $x_0$ jest liczbą niewymierną, $x$ będzie liczbą wymierną) i równocześnie $|f(x)-f(x_0)|=1>1/2=\epsilon$. Oznacza to, że funkcja Dirichleta $f$ jest nieciągła w punkcie $x_0$. Ponieważ liczba $x_0$ była wybrana dowolnie, więc funkcja $f$ jest nieciągła dla każdego argumentu.

Funkcja Thomae

Funkcję Thomae $g$ definiujemy na zbiorze liczb rzeczywistych wzorem $$g(x)= \begin{cases} 1 & \text{jeśli } x=0;\\ 1/q & \text{jeśli } x \text{ daje się przedstawić w postaci ułamka nieskracalnego}\\ & p/q \text{, gdzie } p \text{ jest liczbą całkowitą, a } q \text{ liczbą naturalną;}\\ 0 & \text{jeśli } x \text{ jest liczbą niewymierną.}\\ \end{cases}$$ Definicja ta oznacza na przykład, że $1/3=g(-1/3)=g(1/3)=g(-2/3)=g(2/3)=g(-4/3)=g(4/3)=g(-5/3)=g(5/3)$ itd., oraz $1=g(-1)=g(1)=g(-2)=g(2)=g(-3)=g(3)$ itd., gdyż liczbę całkowitą $p$ można przedstawić w postaci ułamka $p/1$.

Poniżej wykażemy kolejno, że każda liczba niewymierna jest punktem ciągłości funkcji Thomae, oraz że każda liczba wymierna jest punktem nieciągłości funkcji Thomae.

Twierdzenie. Funkcja Thomae jest ciągła dla wszystkich argumentów niewymiernych.

Dowód. Nich $x_0$ będzie liczbą niewymierną i niech $\epsilon$ będzie dowolną liczbą większą od $0$.

Aby wykazać ciągłość funkcji $g$ w punkcie $x_0$, musimy znaleźć taką liczbę $\delta$ większą od 0, że dla każdego $x$ spełniającego nierówność $|x-x_0|<\delta$ zachodzi również nierówność $|f(x)-f(x_0)|<\epsilon$.

Łatwo zauważyć, że istnieje tylko skończenie wiele ułamków postaci $1/q$, większych lub równych $\epsilon$, gdzie $q$ jest liczbą naturalną. Tworzą one dla pewnego $r$ naturalnego zbiór $\{1/r,1/(r-1),\dots,1/1\}$. Każdy ułamek $1/q$ jest wartością funkcji $g$ w punktach, które można zapisać w postaci ułamka nieskracalnego $p/q$. Istotnie, argumenty, dla których funkcja $g$ przyjmuje wartość $1/q$, są pewnymi wielokrotnościami liczby $1/q$. Jest oczywiste, każdy przedział o środku w liczbie $x_0$ będzie zawierał tylko skończenie wiele wielokrotności liczby $1/q$.

Przyjmując odpowiednio małą liczbę $\delta_q$ możemy otrzymać przedział $(x_0-\delta_q,x_0+\delta_q)$, który nie będzie zawierał już żadnej wielokrotności liczby $1/q$.

W ten sposób dla każdej liczby $1/q$ ze zbioru $\{1/r,1/(r-1),\dots,1/1\}$ możemy dobrać przedział $(x_0-\delta_q,x_0+\delta_q)$ nie zawierający żadnej wielokrotności liczby $1/q$. Jeśli teraz przez $\delta$ oznaczymy najmniejszą z liczb $\delta_q$, $q=1,2,\dots,r$, to przedział $(x_0-\delta_q,x_0+\delta_q)$ nie będzie zawierał żadnej wielokrotności żadnej liczby ze zbioru $\{1/r,1/r-1,\dots,1/1\}$.

Dla tak wyznaczonej liczby $\delta$ mamy: jeśli $|x-x_0|<\delta$, to $|g(x)-g(x_0)|=|g(x)|<\epsilon$, co oznacza, że liczba $x_0$ jest punktem ciągłości funkcji Thomae $g$. Ponieważ liczba niewymierna $x_0$ była wybrana dowolnie, więc funkcja Thomae jest ciągła dla każdego argumentu niewymiernego.

Twierdzenie. Funkcja Thomae jest nieciągła dla wszystkich argumentów wymiernych.

Dowód. Niech $x_0$ będzie różną od zera liczbą wymierną daną w postaci ułamka nieskracalnego $p/q$, gdzie $p$ jest liczbą całkowitą, a $q$ liczbą naturalną. Z własności liczb niewymiernych wynika, że bez względu na to, jak małą przyjmiemy dodatnią liczbę $\delta$, w przedziale $(x_0-\delta,x_0+\delta)$ zawsze znajdziemy liczby niewymierne. Oznacza to, że dla każdej dodatniej liczby $\delta$ istnieje taka liczba $x$, że $|x-x_0|<\delta$ i równocześnie $|g(x)-g(x_0)|=|g(x_0)|=1/q>1/2q=\epsilon$, a zatem funkcja Thomae $g$ jest nieciągła w punkcie $x_0$. Ponieważ różna od zera liczba wymierna $x_0$ była wybrana dowolnie, więc funkcja Thomae jest nieciągła dla każdego różnego od zera argumentu wymiernego.

Podobne rozumowanie zastosowane do liczby $x_0=0$ z $\epsilon=1/2$ pozwala wyciągnąć wniosek, że dla każdej dodatniej liczby $\delta$ istnieje taka liczba $x$, że $|x-x_0|<\delta$ i równocześnie $|g(x)-g(x_0)|=|g(x_0)|=1>1/2=\epsilon$. Tym samym udowodniliśmy, że każda liczba wymierna jest punktem nieciągłości funkcji Thomae.

Rosnąca funkcja ciągła dla wszystkich argumentów niewymiernych i nieciągła dla wszystkich argumentów wymiernych.

Na koniec wykażemy, że istnieje rosnąca funkcja określona na zbiorze liczb rzeczywistych, dla której każda liczba niewymierna jest punktem ciągłości, a każda liczba wymierna jest punktem nieciągłości. Wcześniej musimy przypomnieć pewne fakty.

Fakt 1. Liczby wymierne można ustawić w ciąg, który nie pomija żadnej z nich i w którym każda liczba wymierna występuje tylko raz.

Aby się o tym przekonać, rozważmy następującą nieskończoną tablicę ułamków.

Następnie ustawmy liczby z tablicy w następujący ciąg zgodnie z drogą strzałki zaznaczoną w tabeli: $$1, 1/2, 2, 3, (1), 1/3, 1/4, 2/3, 3/2, 4, 5, (2), (1), (1/2), 1/5\dots$$

Opuśćmy teraz wszystkie powtórzenia, dopiszmy po każdej liczbie liczbę do niej przeciwną oraz dorzućmy zero na początku. Otrzymujemy ciąg obejmujący już wszystkie liczby wymierne, przy czym każda występuje tylko raz: $$0,1,-1,1/2,-1/2,2,-2,3,-3,1/3,-1/3,1/4,-1/4,2/3,-2/3,3/2,-3/2\dots$$

Ciąg ten będziemy zapisywać $\{q_n\}_{n=1}^{\infty}$. Czyli na przykład $q_1=0, q_2=1, q_3=-1,q_4=1/2$ itd. Oczywiście nie jest to jedyny ciąg niepowtarzających się wszystkich liczb wymiernych.

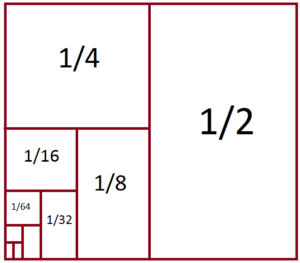
Fakt 2. Następujący nieskończony szereg liczbowy: $1/2+ 1/2^2+ 1/2^3+\dots $ sumuje się do $1$.

Fakt 3. Szereg utworzony z powyższego szeregu przez odrzucenie początkowych składników sumowania aż do składnika $1/2^n$, czyli szereg $1/2^{n+1}+ 1/2^{n+2}+ 1/2^{n+3}+\dots$, sumuje się do $1/2^n$.

Ostatnie dwa fakty można ściśle udowodnić, ale nam niech tu wystarczy obrazowe przedstawienie sumowania liczb jako dodawania pól prostokątów i kwadratów w kwadracie o boku długości $1$:

Twierdzenie. Niech $\{q_n\}_{n=1}^{\infty}$ będzie dowolnym ciągiem niepowtarzających się wszystkich liczb wymiernych. Funkcja $h$ określona na zbiorze liczb rzeczywistych wzorem $$h(x)=\sum\limits_{\{n:\, q_n\leq x\}} 1/2^n$$ jest rosnąca i ciągła tylko dla argumentów niewymiernych.

Uwaga 1. Dokładna analiza poniższego dowodu przekona czytelnika, że ciąg $\{q_n\}_{n=1}^{\infty}$ nie musi wcale składać się ze wszystkich liczb wymiernych. Ciąg $\{q_n\}_{n=1}^{\infty}$ nie musi składać się wyłącznie z liczb wymiernych, a nawet mógłby składać się z samych liczb niewymiernych. Wybraliśmy ciąg złożony z wszystkich liczb wymiernych tylko po to, by twierdzenie ładnie nawiązywało do poprzednich dwóch twierdzeń. Nie jest też naprawdę konieczne, aby liczby w ciągu się nie powtarzały.

Uwaga 2. Wyjaśnijmy, co rozumiemy przez symbol $\sum\limits_{\{n:\, q_n\leq x\}} 1/2^n$. Zbiór $\{n: q_n\leq x\}$ składa się ze wszystkich wskaźników $n$ takich, że dla $q_n$ spełniona jest nierówność $q_n\leq x$. Na przykład zgodnie z naszym określeniem ciągu $\{q_n\}_{n=1}^{\infty}$ do zbioru $\{n: q_n\leq -1/3\}$ należą liczby: $3$ (bo $-1 \leq -1/3$ i $-1$ stoi na trzecim miejscu w ciągu), $5$ (bo $-1/2\leq -1/3$ i $-1/2$ stoi na piątym miejscu), $7$ (bo $-2\leq -1/3$ i $-2$ stoi na siódmym miejscu) i dalej: $9, 11, 15, 17 \dots$ Zapis $\sum\limits_{\{n:\, q_n\leq x\}} 1/2^n$ oznacza więc, że mamy do siebie dodawać wyrażenia $1/2^n$ tylko dla $n$ należących do zbioru $\{3, 5, 7, 9, 11, 15, 17\dots\}$. Stąd $h(-1/3)=1/2^3+1/2^5+1/2^7+1/2^9+1/2^{11}+1/2^{15}+1/2^{17}\dots$

Dowód. Zauważmy najpierw, że funkcja $h$ jest dobrze zdefiniowana, tzn. dla każdego rzeczywistego argumentu $x$ przyjmuje jednoznacznie określoną wartość z przedziału $(0,1)$. Jest tak dlatego, że obliczenie wartości funkcji $h$ w punkcie $x$ polega na zsumowaniu szeregu podobnego do szeregu $1/2+ 1/2^2+ 1/2^3+\dots $, z tą różnicą, że sumujemy tylko pewien wybór składników tego szeregu, a zatem w wyniku otrzymamy liczbę większą od 0, a mniejszą od 1.

Pokażemy, że $h$ jest funkcją rosnącą. Niech $x_1\lt x_2$. Mamy $$h(x_2) – h(x_1) = \sum_{\left\lbrace n: q_n \leq x_2\right\rbrace} \frac{1}{2^n} – \sum_{\left\lbrace n: q_n \leq x_1\right\rbrace} \frac{1}{2^n} = \sum_{\left\lbrace n: x_1 < q_n \leq x_2\right\rbrace} \frac{1}{2^n} > 0$$ Oznacza to, ze większym argumentom odpowiadają większe wartości, co właśnie pokrywa się z definicją funkcji rosnącej.
Następnie pokażemy, że funkcja $h$ jest ciągła dla wszystkich argumentów rzeczywistych, które nie należą do ciągu $\{q_n\}_{n=1}^{\infty}$ . Niech $x_0$ będzie liczbą rzeczywistą, która nie jest elementem ciągu $\{q_n\}_{n=1}^{\infty}$, i niech będzie dana dowolna dodatnia liczba $\epsilon$. Dobierzmy liczbę naturalną $N$ tak, aby była to największa liczba naturalna, dla której jest spełniona nierówność $1/2^N<\epsilon$. Rozważmy pierwsze $N$ wyrazów ciągu $\{q_n\}_{n=1}^{\infty}$, czyli skończony zbiór liczb $\{q_1, q_2, \dots, q_N\}$. Ponieważ zbiór $\{q_1, q_2,\dots, q_N\}$ jest skończony, możemy dobrać tak małą dodatnią liczbę $\delta$, aby w przedziale $(x_0-\delta,x_0+\delta)$ nie znajdowała się żadna liczba ze zbioru $\{q_1, q_2,\dots, q_N\}$. Wówczas dla każdej liczby $x$ nierówność $|x-x_0|<\delta$ pociąga za sobą
$$\begin{split} |h(x)-h(x_0)| &= \sum\limits_{\{n:\, x\lt q_n\leq x_0 \mbox{ lub } x_0\lt q_n\leq x\} } 1/2^n=1/2^{N+1}+1/2^{N+2}+\dots \\ \\ &=1/2^N<\epsilon. \end{split}$$
Zgodnie z definicją ciągłości implikacja ta oznacza, że funkcja $h$ jest ciągła w punkcje $x_0$. Ponieważ $x_0$ była dowolna liczbą rzeczywistą nie należącą do ciągu $\{q_n\}_{n=1}^{\infty}$, więc funkcja $h$ jest ciągła dla wszystkich argumentów nie należących do ciągu wszystkich liczb wymiernych $\{q_n\}_{n=1}^{\infty}$ .

Pozostaje wykazać, że każda liczba, która należy do ciągu $\{q_n\}_{n=1}^{\infty}$, jest punktem nieciągłości funkcji $h$. \\ \\ Niech $x_0$ będzie liczbą należącą do ciągu $\{q_n\}_{n=1}^{\infty}$, powiedzmy $x_0=q_k$ dla pewnej liczby naturalnej $k$. Niech $x$ będzie dowolną liczbą mniejszą od $x_0$. Wówczas mamy
$$\begin{split} |h(x)-h(x_0)| & = \sum\limits_{\{n:\, x\lt q_n\leq x_0\}}1/2^n= \sum\limits_{\{n:\, x\lt q_n\leq q_k\}}1/2^n \\ \\& = 1/2^k+ \sum\limits_{\{n:\, x\lt q_n\lt q_k\}}1/2^n \hspace{.5cm} \geq 1/2^k. \end{split}$$
Otrzymana nierówność $|h(x)-h(x_0)| \geq 1/2^k$ pokazuje, że jeśli przyjmiemy $\epsilon=1/2^k$, to dla każdej dodatniej liczby $\delta$ znajdziemy taką liczbę $x$, że $|x-x_0|<\delta$ i równocześnie $|h(x)-h(x_0)| \geq \epsilon$. Oznacza to, że $x_0$ jest punktem nieciągłości funkcji $h$.

Ponieważ liczba $x_0$ była wybrana dowolnie z ciągu wszystkich liczb wymiernych $\{q_n\}_{n=1}^{\infty}$, więc wnosimy, że funkcja $h$ jest nieciągła dla każdego argumentu wymiernego.

Zakończenie

Przyjrzeliśmy się trzem przykładom „bardzo nieciągłych” funkcji określonych na zbiorze liczb rzeczywistych. Funkcja Dirichleta okazała się nieciągła w każdym punkcie rzeczywistym. Funkcja Thomae była nieciągła we wszystkich punktach niewymiernych, a ciągła we wszystkich punktach wymiernych. Ostatnia, trzecia funkcja była podobna do drugiej, ale dodatkowo okazała się rosnąca. Konstrukcja tej funkcji pozwala zrozumieć, że dowolny zbiór liczb, które można ustawić w skończony lub nieskończony ciąg, może być zbiorem punktów nieciągłości pewnej funkcji niemalejącej, przy czym wszystkie pozostałe punkty jej dziedziny można uczynić jej punktami ciągłości.

Czytelnik może się zastanawiać, czy dałoby się znaleźć przykład funkcji, która – odwrotnie – byłaby nieciągła we wszystkich punktach niewymiernych, a ciągła we wszystkich punktach wymiernych. Zaskakująca być może odpowiedź brzmi: Taka funkcja nie może istnieć! Dowód tego faktu, znacznie trudniejszy od wyżej przytoczonych, wypada jednak odłożyć na inną okazję.