Okrąg dziewięciu punktów – krótkie przypomnienie

Niech $ABC$ będzie trójkątem. Oznaczmy przez $A_H,B_H,C_H$ spodki wysokości opuszczonych z wierzchołków $A,B,C$ odpowiednio. Niech $H$ będzie ortocentrum trójkąta $ABC$. Oznaczmy przez $A’,B’,C’$ środki odcinków $AH,BH,CH$ odpowiednio. Wreszcie, przez $A_G,B_G,C_G$ oznaczmy środki boków $BC,CA$ oraz $AB$. Wtedy twierdzenie Feuerbacha mówi, że punkty $A_H,B_H,C_H,A’,B’,C’$ oraz $A_G,B_G,C_G$ leżą na jednym okręgu, który nazywamy okręgiem dziewięciu punktów. Dokładny opis wraz z dowodem przedstawiła w swoim artykule pt. „Twierdzenie Feuerbacha” Ewa Kosińska.

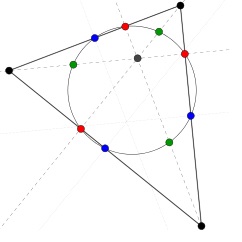
Rysunek 1. Źródło: wikipedia.org

Sfera dwunastu punktów – o jakie punkty właściwie chodzi?

Sfera dwunastu punktów jest przestrzennym odpowiednikiem okręgu dziewięciu punktów. Jeśli przypomnimy sobie konstrukcję tego okręgu, możemy się spodziewać, że czworościan, względem którego będziemy rozważać naszą sferę, będzie ortocentryczny (tzn. że wysokości opuszczone z poszczególnych wierzchołków na przeciwległe ściany przecinają się w jednym punkcie). W przypadku płaskim warunek był spełniony, ponieważ wysokości w dowolnym trójkącie przecinają się w jednym punkcie. W przestrzeni nie musi wcale tak być.

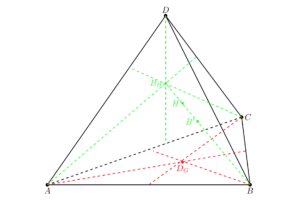
Niech $ABCD$ będzie ortocentrycznym czworościanem, gdzie $H$ jest punktem przecięcia się jego wysokości. Wprowadźmy następujące oznaczenia:

• $A_G,B_G,C_G,D_G$ – środki ciężkości ścian przeciwległych do wierzchołków $A,B,C,D$ (punkty przecięcia się środkowych trójkątów $BCD,CDA,DAB,\\ABC$ odpowiednio),
• $A_H,B_H,C_H,D_H$ – spodki wysokości opuszczonych z wierzchołków $A,B,C,\\D$,
• $A’,B’,C’,D’$ – punkty leżące na odcinkach $AH,BH,CH,DH$ i dzielące je w stosunku $2:1$.

Punkty $A_G,B_G,C_G,D_G,A_H,B_H,C_H,D_H,A’,B’,C’,D’$ leżą wówczas na jednej sferze, którą nazywamy sferą dwunastu punktów.

Dowód

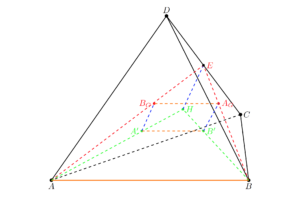
Zauważmy, że $A’B’||AB$ oraz $A’B’=\frac{1}{3}AB$ na mocy twierdzenia odwrotnego do twierdzenia Talesa, ponieważ $A’$ i $B’$ dzielą odcinki $AH$ i $BH$ w stosunku $2:1$ odpowiednio. Podobnie $A_GB_G||AB$ oraz $A_GB_G=\frac{1}{3}AB$, bo $A_G$ i $B_G$ jako środki ciężkości ścian $BCD$ oraz $ACD$ dzielą odpowiednie środkowe w w stosunku $2:1$. Wynika stąd, że $A’B’A_GB_G$ jest równoległobokiem. Pokażemy, że jest to prostokąt.

Oznaczmy przez $E$ środek krawędzi $CD$. Udowodnimy najpierw, że płaszczyzna $CDH$ jest prostopadła do prostej $AB$. $DD_H\perp ABC$, więc każda płaszczyzna zawierająca prostą $DD_H$ jest prostopadła do $ABC$. Jedną z takich płaszczyzn jest $CDH$. Analogicznie pokazujemy, że $CDH\perp ABD$. Zatem $CDH$ jest prostopadła do części wspólnej $ABC$ i $ABD$, którą jest prosta $AB$.

Skoro $CDH$ jest prostopadła do $AB$, to każda prosta leżąca na tej płaszczyźnie musi być prostopadłą do $AB$. W szczególności $EH\perp AB$. Zauważmy, że $A_GB’||EH$. Łącząc to z faktem $A’B’||AB$ stwierdzamy, że $A’B’\perp A_GB’$, czyli istotnie $A’B’A_GB_G$ jest prostokątem. W dowolnym prostokącie przekątne są równe i przecinają się w połowie, więc $A’A_G=B’B_G$. Oznaczmy przez $S$ środek odcinka $A’A_G$. Niech $r=\frac{1}{2}A’A_G$. Wtedy sfera dwunastu punktów czworościanu $ABCD$ ma środek $S$ i promień $r$. Widzimy, że należą do niej punkty $A’,B’,A_G,B_G$.

Analogicznie jak w przypadku $A’B’A_GB_G$ możemy dowieść, że $A’C’A_GC_G$ jest prostokątem, skąd wynika, że punkty $C’$ i $C_G$ należą do sfery o środku $S$ i promieniu $r$. Podobnie jest z punktami $D’$ oraz $D_G$.

Każdy z trójkątów $AA_HA_G,BB_HB_G,CC_HC_G,DD_HD_G$ jest prostokątny, więc okręgi opisane na tych trójkątach mają środek $S$ i promień $r$. Są to koła wielkie naszej sfery, co kończy dowód.