Czy zastanawiałeś się pod jakim kątem należy rzucić piłkę, żeby uderzyła w ziemię jak najdalej? Płaski tor rzutu spowoduje, że piłka nie wykorzysta całej prędkości. Celując wyżej możemy dorzucić piłkę dalej, natomiast jeśli przesadzimy wzbije się ona wysoko, ale spadnie tuż przy nas.

Z odpowiedzią na to pytanie przychodzi analityczne spojrzenie na tor lotu obiektu. W naszych rozważaniach pomijamy opór powietrza.

Analityczny opis toru lotu

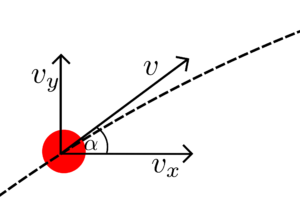
Spójrzmy na lecącą piłkę z boku. Położenie piłki możemy opisać za pomocą współrzędynch $x$ oraz $y$, które będą zależały od czasu $t$. W chwili początkowej $t_0=0$ piłka będzie zaczynała ruch i znajdowała się tuż przy ziemi. Wtedy również $x=0$ oraz $y=0$. Piłka będzie leciała w prawo oraz początkowo będzie wznosiła się w powietrze, aby następnie zacząć opadać.

Lecący w powietrzu obiekt będzie miał pewną prędkość $v$, której wektor skierowany jest pod pewnym kątem $\alpha$ do powierzchni ziemi. Wektor prędkości $v$ rozbijamy na 2 składowe $v_x$ (poziomą) oraz $v_y$ (pionową).

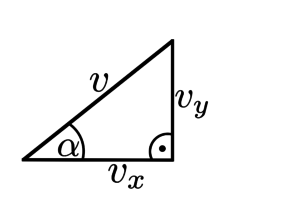
Końce wektorów $v_x$, $v$ wraz z punktem ich wspólnego początku tworzą trójkąt prostokątny. Korzystając ze wzorów trygonometrycznych dostajemy $cos(\alpha) = \frac{v_x}{v}$, czyli $v_x = vcos(\alpha)$. I podobnie $sin(\alpha) = \frac{v_y}{v}$, co daje $v_y = vsin(\alpha)$.

W chwili początkowej $t_0=0$ (kiedy $x=0$ i $y=0$) ustalamy że mamy kąt $\alpha_0$ oraz prędkość $v_0$ ze składowymi $v_{0x}$, $v_{0y}$.

Prędkość pozioma $v_x$ nie bedzie zmieniać się w żadnym punkcie trajektorii lotu, ponieważ jedyna siła działająca na nasz obiekt to siła grawitacji skierowana prostopadle do wektora prędkości $v_x$. Tak więc funkcja zależności położenia $x$ od czasu $t$ będzie dana wzorem $x(t) = v_{0x} t$ jak w każdym ruchu jednostajnym prostoliniowym. Podstawiając $v_0cos(\alpha)$ pod $v_{0x}$ dostaniemy $x(t) = v_0tcos(\alpha_0)$.

Siła grawitacji oddziaływać będzie natomiast na prędkość pionową. Ze względu na obecność przyśpieszenia grawitacyjnego ruch pionowy będzie ruchem jednostajnie przyśpieszonym z prędkością początkową $v_{0y}$ oraz przyśpieszeniem grawitacyjmy $-g$. Minus wynika z tego, że przyśpieszenie grawitacyjne skierowane jest „w „dół” osi $y$. Zależność wysokości $y$ od czasu $t$ wyrazimy wzorem na położenie w ruchu jednostajnie przyśpieszonym, czyli $y(t) = v_{0y}t – \frac{gt^2}{2}$. Podstawiając $v_0sin(\alpha_0)$ pod $v_{0y}$ dostaniemy $y(t) = v_0tsin(\alpha_0) – \frac{gt^2}{2}$.
Mamy już równania ruchu:
$$\begin{align*}x(t) &= v_0tcos(\alpha_0)\\ y(t) &= v_0tsin(\alpha_0) – \frac{gt^2}{2}\end{align*}$$

Największy zasięg

Znamy już funkcje $x$ i $y$. Ruch obiektu będzie trwał tak długo jak długo współrzędna $y$ będzie większa od zera. W chwili uderzenia obiektu o ziemię $t_k$ będziemy mieli $y(t_k)=0$. Musimy zatem znaleźć takie $t_k$, że $y(t_k)=0$.
$$\begin{align*}y(t) &= 0 \\ v_0tsin(\alpha_0) – \frac{gt^2}{2} &= 0 \\ 2v_0tsin(\alpha_0) – gt^2 &= 0 \\ t\left( 2v_0sin(\alpha_0) – gt \right) &= 0 \end{align*}$$
Dostajemy, że $t=0$ albo $\left(2v_0sin(\alpha_0) – gt \right)=0$. Pierszy przypadek to $t_0$, czyli początku ruchu. Drugi przypadek zachodzi
w momencie uderzenia o ziemię, więc będzie to $t_k$.
$$\begin{align*}2v_0sin(\alpha_0) – gt &= 0 \\ gt &= 2v_0sin(\alpha_0) \\ t &= \frac{2v_0sin(\alpha_0)}{g} \end{align*}$$

Mamy czas końcowy $t_k = \frac{2v_0sin(\alpha_0)}{g}$. Warto zauważyć, że jest to całkowity czas trwania lotu. Podstawiamy $t_k$ do wzoru
na współrzędną poziomą $x$.
$$\begin{align*}x(t) &= v_0tcos(\alpha_0) \\ x(t_k) &= v_0 \frac{2v_0sin(\alpha_0)}{g}cos(\alpha_0) \\ x(t_k) &= \frac{v_0^22sin(\alpha_0)cos(\alpha_0)}{g} \\ x(t_k) &= \frac{v_0^2sin(2\alpha_0)}{g} \end{align*}$$
Ostatnie przekształcenie wynika ze wzoru na sinus kąta podwójnego $sin(2\alpha_0) = 2sin(\alpha_0)cos(\alpha_0)$.

Wiemy już, że zasięg rzutu możemy obliczyć ze wzoru $x(t_k) = \frac{v_0^2sin(2\alpha_0)}{g}$. Teraz chcemy dowiedzieć się jak dobrać kąt $\alpha_0$ tak, żeby wartość $x(t_k)$ była największa.

Wyrażenie $\frac{v_0^22sin(2\alpha_0)}{g}$ będzie tym większe, im większy będzie $sin(2\alpha_0)$. Oczywiście największą wartość jaką może osiągnąć sinus to $1$ i jest ona osiągana dla kąta równego $90$ stopni, gdy pytamy się o kąt pomiędzy $0$ a $360$ stopni.
$$\begin{align*}sin(2\alpha_0) &= 1 \\ 2\alpha_0 &= 90^{\circ} \\ \alpha_0 &= 45^{\circ}\end{align*}$$

Otrzymujemy odpowiedź, że najbardziej optymalny kąt dla rzutu to kąt $45$ stopni.

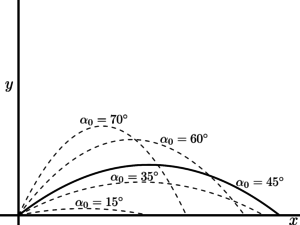
Poniżej zaobserwować można wpływ kąta początkowego $\alpha_0$ na zasięg rzutu.

Maksymalna wysokość

Zastanówmy się pod jakim kątem należy rzucić piłkę żeby doleciała jak nawyżej. Intuicja podpowiada nam, że powinniśmy rzucić piłkę pionowo. Przedstawimy matematyczne uzasadnienie tego stwierdzenia przy okazji znajdując maksymalną wysokosć $y$ w torze lotu obiektu w zależności od dowolnego kąta początkowego $\alpha_0$ i prędkości początkowej $v_0$.

Równanie współrzędnej $y(t) = v_0tsin(\alpha_0) – \frac{gt^2}{2}$ jest równaniem kwadratowym zmiennej $t$. Ponieważ współczynnik $-\frac{g}{2}$ przy $t^2$ jest ujemny, funkcja $y$ jest wypukła i wierzchołek będzie największym punktem trajektorii. Korzystamy ze wzoru na pierwszą współrzędną wierzchołka $t_h$ wypukłej funkcji kwadratowej $y=at^2 + bt +c$, aby znaleźć czas, w którym osiągana jest największa wysokość:

$$\begin{align*} t_h & = -\frac{b}{2a} \\ \\ t_h &= -\frac{2v_0sin(\alpha_0)}{2\left(-\frac{g}{2}\right)}\\ t_h& = \frac{v_0sin(\alpha)}{g} \end{align*}$$

Podstawiamy czas $t_h$ do wzoru na współrzędną $y$:

$$\begin{align*}y(t) &= v_0tsin(\alpha_0) – \frac{gt^2}{2} \\ y(t_h) &= v_0\frac{v_0sin(\alpha)}{g}sin(\alpha_0) – \frac{g\left(\frac{v_0sin(\alpha)}{g}\right)^2}{2} \\ y(t_h) &= \frac{v_0^2sin^2(\alpha_0)}{g} – \frac{v_0^2sin^2(\alpha_0)}{2g} \\ y(t_h) &= \frac{v_0^2sin^2(\alpha_0)}{g} \end{align*}$$
Ponieważ sinus osiąga maksymalną wartość dla kąta równego $0$ stopni (jeśli mówimy o kątach między $0$ a $360$ stopni), to wyrażenie $y(t)$ osiągnie najwyższą wartość dla $\alpha_0=90^{\circ}$ .

Podsumowanie

Ostatecznie przy oznaczeniach $t_k$- czas końcowy, $t_h$- czas dla którego osiągana jest maksymalna wysokość, otrzymaliśmy następujące wzory:

$$\begin{align*} x(t)&= v_0tcos(\alpha_0) \\ y(t) &= v_0tsin(\alpha_0) – \frac{gt^2}{2}\\ t_k &= \frac{2v_0sin(\alpha_0)}{g} \\ x(t_k) &= \frac{v_0^2sin(2\alpha_0)}{g} \\ t_h &= \frac{v_0sin(\alpha_0)}{g} \\ y(t_h) &= \frac{v_0^2sin^2(\alpha_0)}{g} \\ \end{align*}$$

Ten artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną z Fundacji mBanku na realizację projektu „Potęga matematyki”.