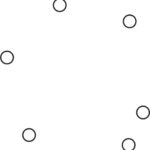
Ustalmy sześć punktów na płaszczyźnie i każdy odcinek łączący parę z tych punktów pokolorujmy na jeden z dwóch kolorów. Czy znajdziemy w tym układzie jednokolorowy trójkąt? Jeśli tak, to czy w układzie z większą liczbą punktów połączonych kolorowymi odcinkami znajdziemy coś innego, większego, ciekawego i jednokolorowego? A czy może wystarczy pięć punktów, aby znaleźć jednokolorowy trójkąt? Wyjmij kredki, kartkę i zacznij czytać − dowiesz się co nieco o teorii Ramseya.
Krok pierwszy
Dawno, dawno temu1, w roku szkolnym 1965/66, na XVII Olimpiadzie Matematycznej pojawiło się następujące zadanie.
Zadanie [XVII OM − Etap II − Zadanie 3]
Na płaszczyźnie obrano sześć punktów, z których żadne trzy nie leżą na jednej prostej i wykreślono wszystkie odcinki łączące parami te punkty. Niektóre z odcinków wykreślono przy tym kolorem czerwonym, a inne niebieskim. Dowieść, że któreś trzy z danych punktów są wierzchołkami trójkąta o bokach jednego koloru.
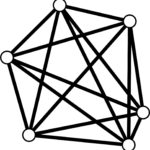
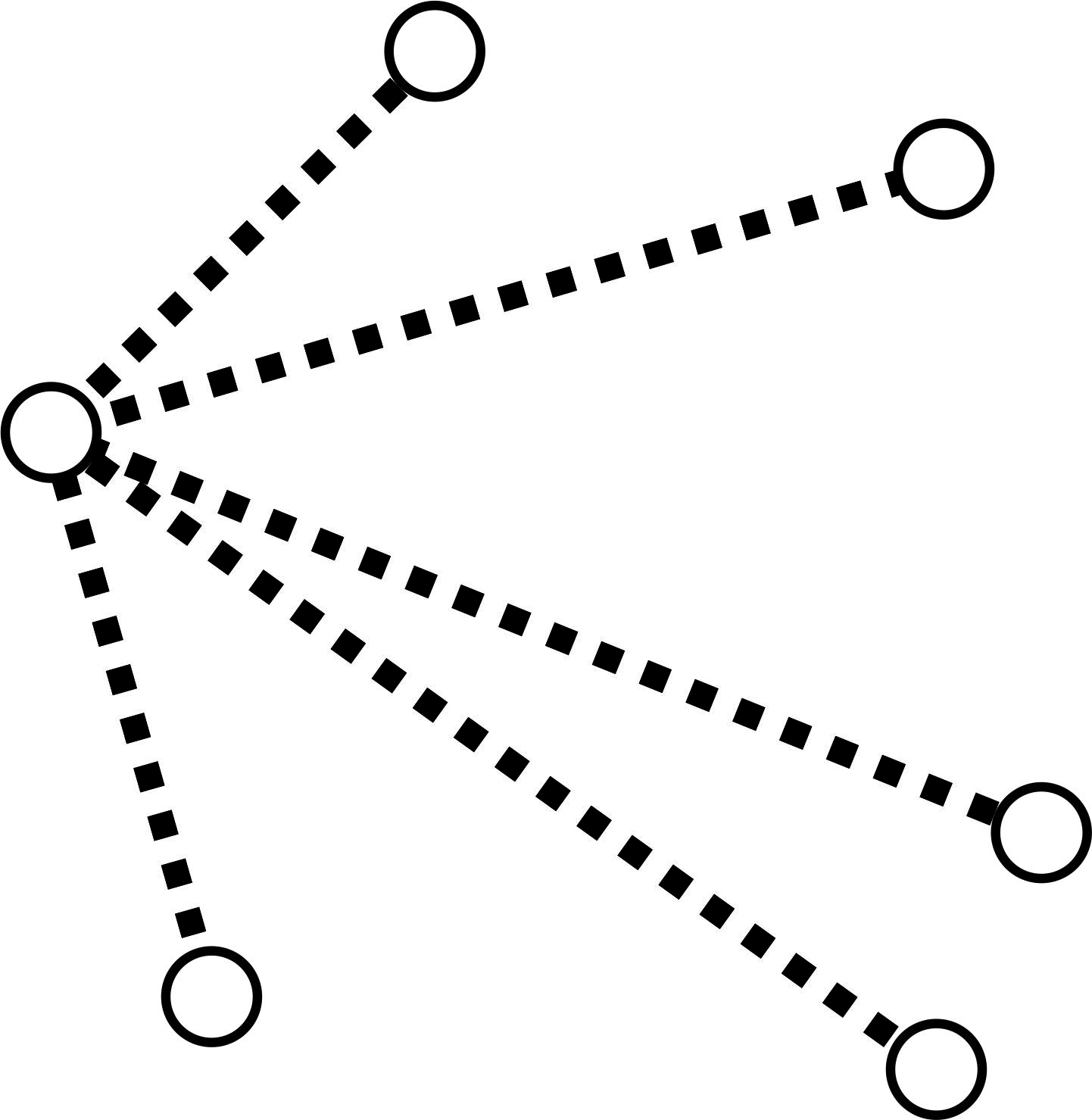
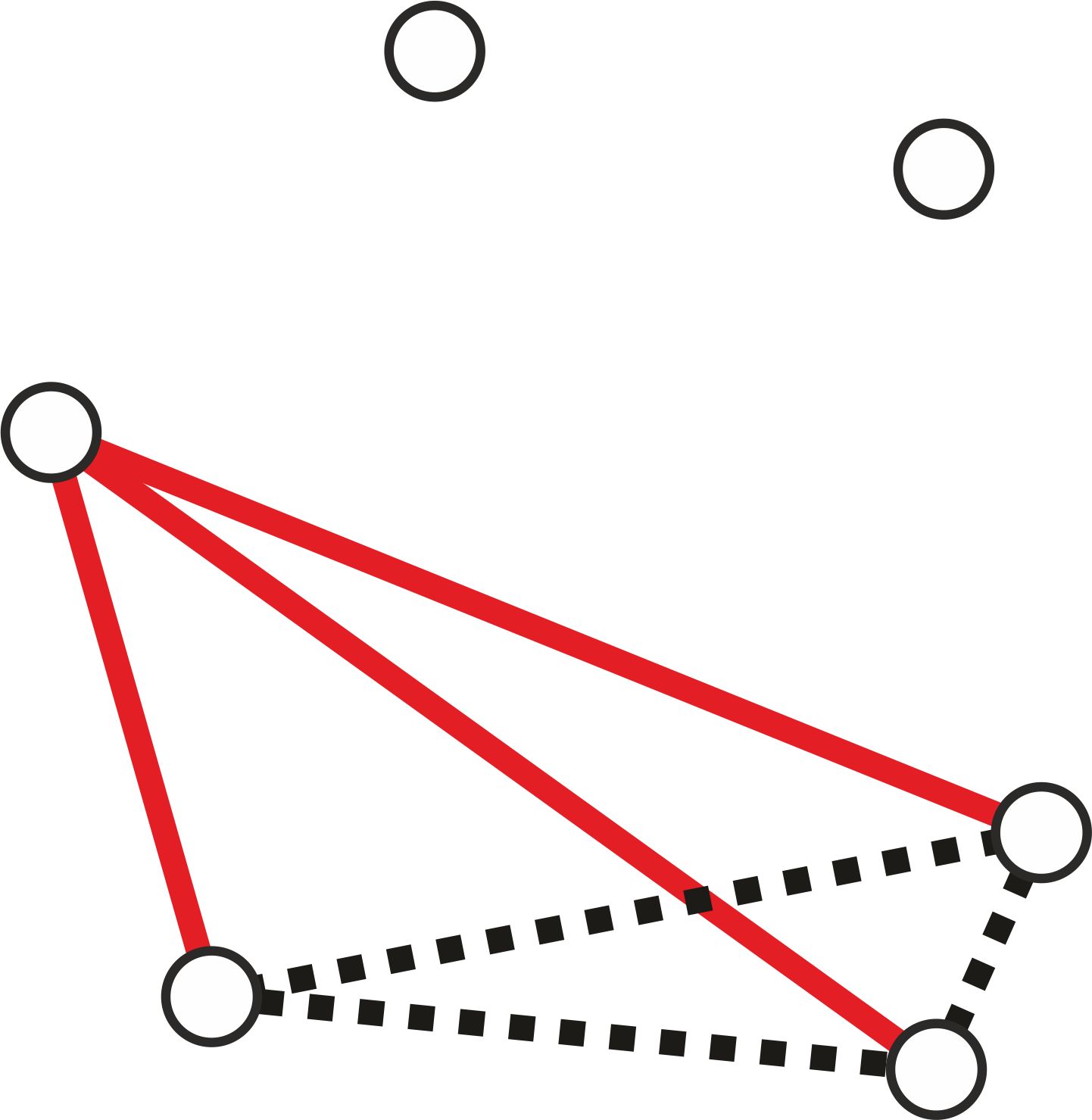
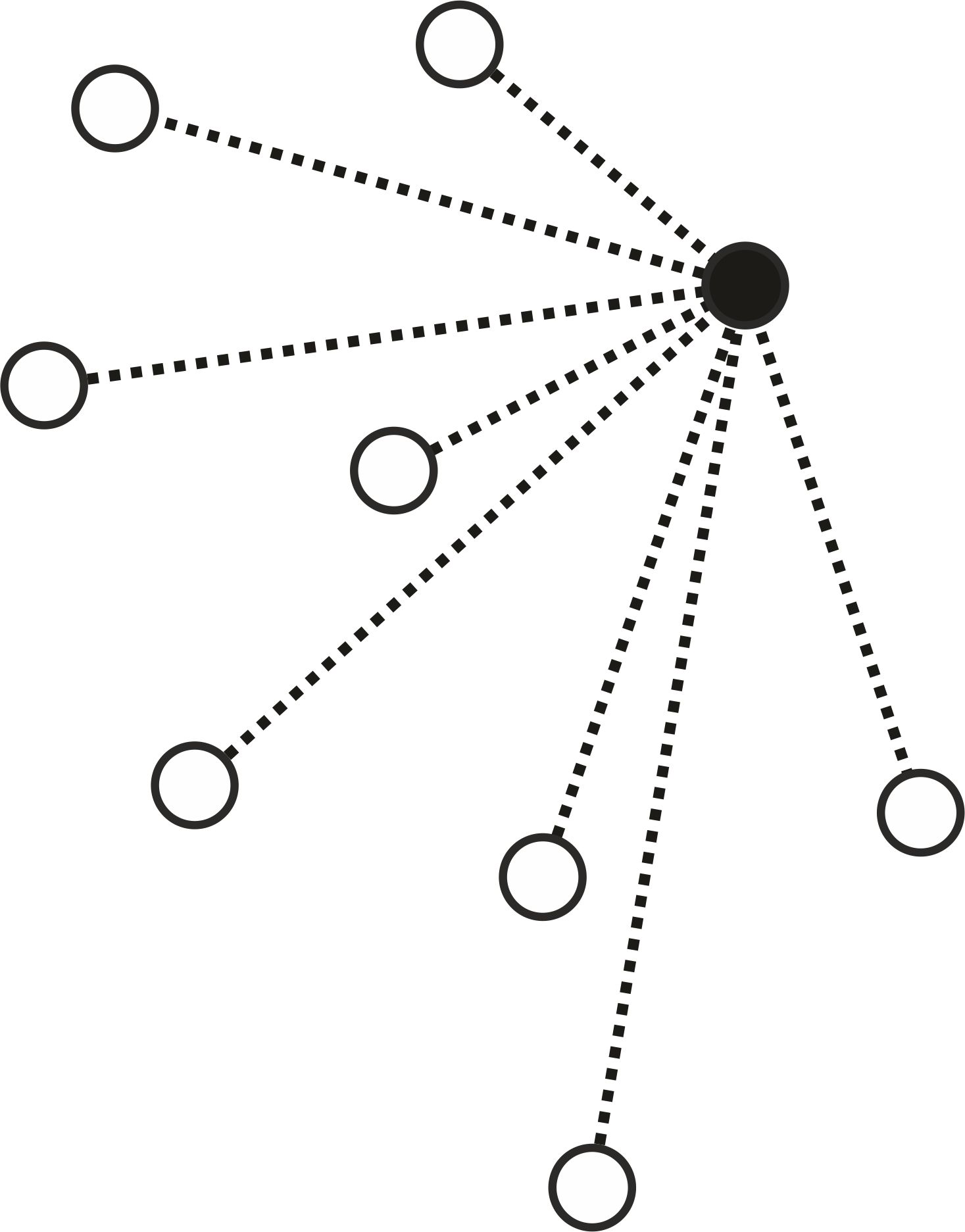
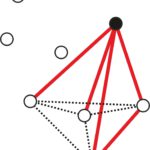
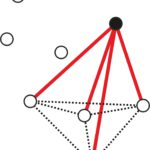
Rozwiązanie. Ustalmy dowolny punkt i odcinki łączące go z pozostałymi pięcioma punktami (zobacz rysunek poniżej). Zauważmy, że pewne (co najmniej trzy) z tych odcinków są czerwone albo pewne (ale co najmniej trzy) są niebieskie. Jeśli by tak nie było to co najwyżej dwa odcinki byłyby czerwone i co najwyżej dwa niebieskie, czyli byłyby co najwyżej cztery odcinki.
Zauważmy, że co najmniej trzy z tych odcinków są czerwone albo co najmniej trzy są niebieskie. Załóżmy więc, że pewne trzy są czerwone.2 Te czerwone odcinki łączą ustalony na początku punkt z trzema innymi punktami, które tworzą trójkąt (patrz rysunek).
Ten trójkąt jest albo niebieski (wtedy istnieje jednokolorowy niebieski trójkąt), albo pewien z jego boków jest czerwony (wtedy ten bok z odcinkami wychodzącymi ustalonego na początku punktu tworzą czerwony trójkąt). Stąd wynika, że istnieje jednokolorowy trójkąt.
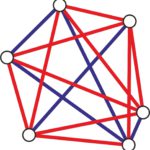
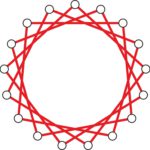
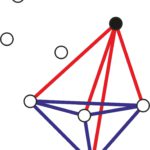
Czy liczba sześciu wierzchołków jest jakoś specjalnie wyróżniona? Czy w przypadku pięciu punktów można tak pokolorować odcinki, żeby uniknąć jednokolorowego trójkąta. Odpowiedź jest pozytywna, wystarczy spojrzeć na ilustrację poniżej.
Co zatem możemy wywnioskować na podstawie rozwiązania powyższego zadania?
Stwierdzenie 1
Dla dowolnego układu \(n\) punktów na płaszczyźnie (takiego, że żadne trzy z nich nie są współliniowe), w którym każdy łączący dwa punkty odcinek możemy pokolorować albo na niebiesko albo na czerwono
- jeśli \(n < 6\), to istnieje pokolorowanie wszystkich odcinków, w którym nie ma jednokolorowego trójkąta;
- jeśli \(n\ge 6\), to każde pokolorowanie wszystkich odcinków ma jednokolorowy trójkąt.
Zauważmy, że aby pokazać 1. wystarczy podać przykład pokolorowania bez trójkątów. Natomiast w dowodzie 2. musimy uwzględnić wszystkie możliwe pokolorowania. Liczba 6 jest liczbą Ramseya \(R(3,3)\), ale o tym porozmawiamy później.
O jeden krok dalej
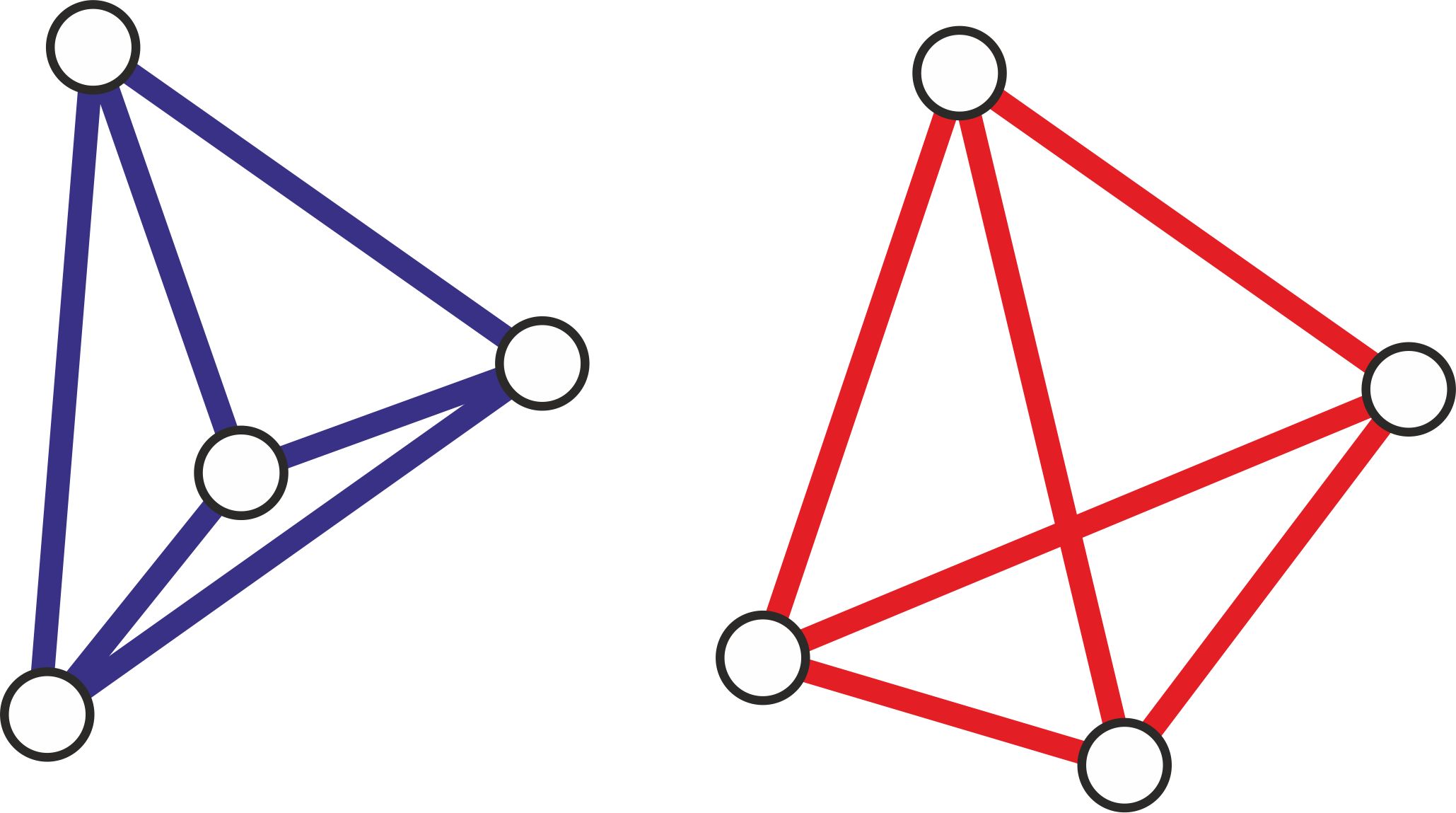
Problem jednokolorowych trójkątów już zgłębiliśmy. Nie chcemy jednak spocząć na laurach, więc zerkniemy na problem jednokolorowych czworokątów. Czworokąt (niekoniecznie wypukły) będziemy uznawać za jednokolorowy, gdy wszystkie jego boki i przekątne (niekoniecznie wewnątrz czworokąta) są tego samego koloru. Właściwie z tego wynika, że jednokolorowym czworokątem będziemy nazywać układ czterech punktów parami połączonych odcinkami o tym samym kolorze. Przykłady jednokolorowych czworokątów można znaleźć na poniższym rysunku.
Sformułujemy zagadnienie, którym zajmować się będziemy w tym paragrafie.
Problem
Umieszczamy na płaszczyźnie \(n\) punktów (tak, że żadne trzy z nich nie są współliniowe) i pokolorujemy każdy łączący je odcinek − albo na niebiesko, albo na czerwono. Czy istnieje taka liczba naturalna \(R(4,4)\), że
- jeśli \(n < R(4,4)\), to możemy pokolorować odcinki tak, aby uniknąć jednokolorowego czworokąta?
- jeśli \(n\geqslant R(4,4)\), to przy każdym pokolorowaniu istnieje jednokolorowy czworokąt?
W tym przypadku sprawa nie jest już taka prosta, ale spróbujemy sobie z nią poradzić. Przypomnijmy, że aby pokazać 1. wystarczy podać przykład pokolorowania bez jednokolorowych czworokątów. Natomiast w dowodzie punktu 2. musimy uwzględnić wszystkie możliwe pokolorowania.
Zacznijmy od punktu 2., przypominając co robiliśmy w poprzednim paragrafie:
- Najpierw wybraliśmy jeden punkt.
- Następnie zauważyliśmy, że wychodzą z niego odcinki jednego koloru do co najmniej trzech innych punktów.
- Na końcu wykorzystaliśmy fakt, że trzy punkty tworzą trójkąt niebieski albo zawierają jeden odcinek czerwony (lub analogiczny fakt, że trzy punkty tworzą trójkąt czerwony albo zawierają jeden odcinek niebieski).
Cała trudność polega na znalezieniu analogu faktu przedstawionego w punkcie 3. Oto on.
Fakt 1
Jeśli umieścimy dziewięć punktów na płaszczyźnie (tak, że żadne trzy z nich nie są współliniowe) i pokolorujemy każdy łączący je odcinek albo na niebiesko albo na czerwono, to zawsze znajdziemy w tym układzie czerwony trójkąt lub niebieski czworokąt.
Oczywiście można zamienić czerwony na niebieski i niebieski na czerwony w kolorowaniach w dowodzie Faktu 1, zatem prawdziwy jest też poniższy fakt.
Fakt 1′
Jeśli umieścimy dziewięć punktów na płaszczyźnie (tak, że żadne trzy z nich nie są współliniowe) i pokolorujemy każdy łączący je odcinek albo na niebiesko albo na czerwono, to zawsze znajdziemy w tym układzie czerwony czworokąt lub niebieski trójkąt.
Dowód powyższych faktów jest bardzo podobny do dowodu Stwierdzenia 1 z poprzedniego paragrafu oraz do dowodu, który zaprezentujemy za chwilę. Z pewnych względów jest on jednak o wiele bardziej skomplikowany. Zainteresowane osoby mogą go przeczytać pod koniec niniejszego tekstu.
Spróbujmy powtórzyć dowód Stwierdzenia 1 z poprzedniego paragrafu z wykorzystaniem Faktów 1 i 1′. Przez analogię (bo \(R(3,3)=3+3\), gdzie 3 to jest liczba z faktu w pkt. 3), spodziewamy, się, że \(R(4,4)=18\) powinno nam wystarczyć (bo \(18=9+9\), gdzie \(9\) jest liczbą z Faktu 1).
- Najpierw wyróżnijmy dowolny punkt spośród 18 punktów umieszczonych na płaszczyźnie.
- Z wyróżnionego punktu wychodzi co najmniej dziewięć odcinków czerwonych lub co najmniej dziewięć odcinków niebieskich. Załóżmy, że jest to dziewięć czerwonych odcinków3.
- Istnieje zatem dziewięć punktów, które są połączone z wyróżnionym punktem czerwonymi odcinkami. Z Faktu 1 wśród tych punktów jest niebieski czworokąt (mamy wtedy niebieski czworokąt) lub czerwony trójkąt (wtedy punkty tego trójkąta z wyróżnionym punktem tworzą czerwony czworokąt). Zatem wśród wszystkich 18 punktów istnieje jednokolorowy czworokąt.
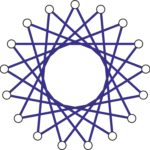
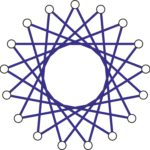
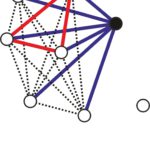
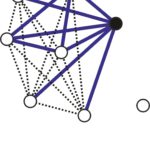
Możemy postawić hipotezę, że \(R(4,4)=18\). Aby ją wykazać musimy dowieść 1., tzn. że istnieje pokolorowanie odcinków łączących 17 punktów bez jednokolorowego czworokąta. Niestety rysunek kolorowania byłby kompletnie nieczytelny, więc rozbiliśmy go na kilka rysunków, na których pokazujemy, które odcinki pokolorować na niebiesko a które na czerwono.
Krawędzie czerwone:
Krawędzie niebieskie
Ostatecznie wykazaliśmy następujące stwierdzenie.
Stwierdzenie 2
Dla dowolnego układu \(n\) punktów na płaszczyźnie (takiego, że żadne trzy z nich nie są współliniowe), w którym każdy łączący dwa punkty odcinek możemy pokolorować albo na niebiesko albo na czerwono
- jeśli \(n < 18=R(4,4)\), to istnieje pokolorowanie wszystkich odcinków, w którym nie ma jednokolorowego czworokąta;
- jeśli \(n\ge 18=R(4,4)\), to każde pokolorowanie wszystkich odcinków ma jednokolorowy czworokąt.
Wkładamy siedmiomilowe buty
Skoro udało nam się z trójkątami i czworokątami, można by się pokusić o ogólne stwierdzenie. Zdefiniujmy jednokolorowy \(k\)-kąt jako układ \(k\) punktów na płaszczyźnie, które wszystkie parami są połączone odcinkami tego samego koloru.
Twierdzenie Ramseya
Dla dowolnej liczby całkowitej \(k\geqslant 3\) istnieje liczba całkowita \(R(k,k)\) o takiej własności, że w dowolnym układzie \(n\) punktów na płaszczyźnie (takim, że żadne trzy z punktów nie są współliniowe), w którym kolorujemy każdy łączący dwa punkty odcinek albo na niebiesko albo na czerwono
- jeśli \(n < R(k,k)\), to istnieje pokolorowanie odcinków, w którym nie ma jednokolorowego \(k\)-kąta;
- jeśli \(n\geqslant R(k,k)\), to każde pokolorowanie odcinków ma jednokolorowy \(k\)-kąt.
Zauważmy, że Powyżej nie tylko pokazaliśmy prawdziwość tego stwierdzenia dla \(k=3\) i \(k=4\), ale także dodatkowo wyznaczyliśmy w tych przypadkach wartość \(R(k,k)\). W 1930 roku pojawił się artykuł, w którym Frank Ramsey udowodnił powyższe twierdzenie dla dowolnego \(k\). Bardzo ciekawskim możemy podpowiedzieć, że można udowodnić je podążając za dowodem Faktu 1 lub części 2. Stwierdzeń 1 i 2. Uwaga: nie jest już w tym dowodzie istotna wartość \(R(k,k)\), tylko fakt, że ona istnieje.
Wróćmy na chwilkę do wartości \(R(k,k)\), którą nazywamy liczbą Ramseya. Dość łatwo udało się nam określić \(R(3,3)\) i \(R(4,4)\). Napawa to optymizmem. Jednak na tym kończy się łatwa część. Dla zobrazowania tego, zacytujmy Paula Erdősa, jednego z najbardziej twórczych matematyków XX wieku.
[…] wyobraźmy sobie, że pewne pozaziemskie siły, niezmiernie bardziej potężne niż nasze, wylądowały na ziemi i domagają się wyznaczenia \(R(5,5)\), albo zniszczą planetę. W tym przypadku, […], powinniśmy zmobilizować wszystkie komputery i matematyków, aby wyznaczyć tę liczbę. Załóżmy jednak, że kosmici zażądają wartości \(R(6,6)\). W tym przypadku, […], powinniśmy spróbować zniszczyć kosmitów.4
Dla poparcia tego stwierdzenia podamy najlepsze znane oszacowania na najmniejsze z liczb Ramseya
\begin{align*}
43\leqslant R(5,5)\leqslant 49;\\
102\leqslant R(6,6)\leqslant 165;\\
205\leqslant R(7,7)\leqslant 540.
\end{align*}
Na koniec skupmy się nad tym, o czym właściwie mówi twierdzenie Ramseya. Rozważmy pewną dowolną strukturę (na przykład dowolne kolorowanie odcinków łączących punkty). Istota powyższego twierdzenia polega na uzasadnieniu, że jeśli owa struktura jest w pewnym sensie duża (na przykład ma dużo punktów), to znajdziemy w niej pewną regularność (na przykład jednokolorowy \(k\)-kąt). Podsumowując, twierdzenie Ramseya jest przykładem na to, że w pewnych dużych strukturach nieunikniona jest pewna regularność. Takimi właśnie problemami zajmuje się teoria Ramseya. Pytania tego typu nie dotyczą tylko punktów i łączących ich odcinków, ale bardziej ogólnych obiektów, jak na przykład grafy, hipergrafy, rodziny podzbiorów, zbiory liczb naturalnych itp. W tym artykule zrobiliśmy tylko trzy pierwsze kroki po szerokich rozdrożach teorii Ramseya. Mamy nadzieję, że znajdą się zainteresowani dalszą eksploracją.
Dowód Faktu 1
Dowód będzie przebiegał analogicznie do dowodów Stwierdzeń 1 i 2 (czyli składać się będzie z trzech kroków).
Ustalmy dziewięć punktów (trójkami niewspółliniowych) na płaszczyźnie i pokolorujmy łączące je odcinki.
- W tym przypadku musimy bardzo ostrożnie wybrać wierzchołek wyróżniony. Najpierw pokażemy, że istnieje punkt, z którego wychodzi parzysta liczba czerwonych odcinków.Załóżmy, że jest inaczej, tzn. że z każdego punktu wychodzi nieparzysta liczba czerwonych odcinków. Oznaczmy liczbę czerwonych odcinków wychodzących z poszczególnych punktów przez \(d_1,d_2,\ldots,d_9\). Każda z tych liczb jest nieparzysta. Z jednej strony, \(d_1+\ldots+d_9\) jest liczbą nieparzystą (jako suma nieparzystej liczby nieparzystych składników). Z drugiej strony, jeśli zsumujemy po kolei liczby czerwonych odcinków wychodzące z punktów, to każdy czerwony odcinek z rysunku będzie policzony dokładnie dwa razy (bo wychodzi z dwóch punktów). Z tego wynika, że \(d_1+\ldots+d_9\) jest liczbą parzystą. Zatem z jednej strony \(d_1+\ldots+d_9\) jest nieparzysta, a z drugiej parzysta. Założenie, że nie ma punktu o wychodzącej parzystej liczbie czerwonych odcinków doprowadziło do sprzeczności, więc musi istnieć jakiś punkt, z którego wychodzi parzysta liczba czerwonych odcinków.Wybierzemy pewien punkt o parzystej liczbie wychodzących czerwonych odcinków i oznaczmy go jako czarny.
- Wiemy, że z czarnego punktu wychodzi osiem odcinków do ośmiu innych punktów. Zatem albo co najmniej sześć z tych odcinków jest niebieskich albo co najmniej trzy są czerwone.
- Rozważmy najpierw przypadek, w którym czarny wierzchołek jest połączony sześcioma niebieskimi odcinkami z pewnymi sześcioma innymi punktami. Ze Stwierdzenia 1 wśród tych punktów jest czerwony trójkąt lub niebieski trójkąt. Jeśli ten trójkąt jest czerwony, to wśród wszystkich dziewięciu punktów jest czerwony trójkąt. Jeśli ten trójkąt jest niebieski, to wraz z czarnym punktem tworzy on niebieski czworokąt.
- W drugim przypadku z czarnego punktu wychodzą co najmniej trzy czerwone odcinki do co najmniej trzy innych punktów. Przypomnijmy jednak, że liczba czerwonych odcinków wychodzących z czarnego punktu jest parzysta, więc punktów połączonych czerwonymi odcinkami z czarnym punktem musi być co najmniej cztery. Wtedy albo te cztery punkty tworzą niebieski czworokąt albo pewien odcinek jest czerwony i wraz z wyróżnionym czarnym punktem tworzy trójkąt.
Czyli ostatecznie udowodniliśmy, że w każdym przypadku wśród dziewięciu punktów z pokolorowanymi odcinakami znajdziemy czerwony trójkąt lub niebieski czworokąt. Ostatecznie w każdym przypadku jest czerwony trójkąt lub niebieski czworokąt.
Co jeszcze można przeczytać
Na deser warto polecić lekturę miesięcznika Delta, a w szczególności zapraszamy do przeczytania tego tekstu.
Przypisy
- Oczywiście jest to dawno temu dla młodego czytelnika, do którego jest adresowany ten artykuł. Przepraszamy starszych czytelników, którzy mogli się poczuć urażeni.
- Gdyby były niebieskie, to możemy rozumować tak samo, tyle tylko, że zamieniamy czerwony na niebieski i niebieski na czerwony.
- W drugim przypadku dowód przebiega analogicznie − wystarczy tylko zamienić niebieski na czerwony i czerwony na niebieski.
- W oryginale: […] imagine an alien force, vastly more powerful than us, landing on Earth and demanding the value of \(R(5,5)\) or they will destroy our planet. In that case, […], we should marshal all our computers and our mathematicians and attempt to find the value. Suppose, instead, that they ask for \(R(6,6)\). In that case, […], we should attempt to destroy the aliens.
Artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu „Potęga matematyki”.