Od wczesnych szkolnych lat i początków edukacji matematycznej towarzyszy nam pojęcie funkcji. Na samym początku w odniesieniu do funkcji liniowej, wraz ze wzrostem metryczki, poznajemy kolejne przykłady (m.in. funkcje kwadratowe, wielomiany, funkcje wymierne, a nawet funkcje trygonometryczne).

Zdecydowana większość przykładów to funkcje ciągłe. Dla wielu z nich w każdym punkcie wykresu można narysować styczną. Dość łatwo wyobrazić sobię funkcję, która ma na wykresie jeden taki punkt, że w tym punkcie nie istnieje styczna¹. Znacznie trudniej o przykład funkcji ciągłej niemającej stycznej w żadnym punkcie wykresu. W tekście wskażemy właśnie takie odwzorowanie, pochodzące od japońskiego matematyka Teiji Takagiego².

O funkcjach ciągłych

Przypomnijmy, że napis \(f\colon A\to B\) oznacza, że funkcja \(f\) odwzorowuje zbiór \(A\) (nazywamy dziedziną funkcji) w zbiór \(B\) (nazywany przeciwdziedziną funkcji). Oznacza to, że każdemu elementowi zbioru \(A\) przypisana jest dokładnie jedna wartość ze zbioru \(B\). Elementy zbioru \(A\) nazywać będziemy argumentami funkcji, a odpowiadające im elementy zbioru \(B\) — wartościami funkcji. W artykule zajmować się będziemy funkcjami, których dziedziną jest zbiór \(\mathbb{R}\) lub jego podzbiór, a przeciwdziedziną zbiór \(\mathbb{R}\). Funkcje tego typu czytelnicy poznali zapewne w czasie edukacji szkolnej. Poniżej prezentujemy kilka przykładów.

• funkcja liniowa: \(f\colon \mathbb{R}\to\mathbb{R}\), \(f(x)=x+1\), \(x\in\mathbb{R}\)
• funkcja kwadratowa: \(f\colon\mathbb{R}\to\mathbb{R}\), \(f(x)=x^2+x+1\), \(x\in\mathbb{R}\)
• funkcja tangens: \(f\colon (-\pi/2,\pi/2)\to\mathbb{R}\), \(f(x)=\operatorname{tg}(x)\), \(x\in(-\pi/2,\pi/2)\).

Na funkcjach warto i należy się znać. Znaczna część zastosowań matematyki (również w naszym codziennym życiu) korzysta z pojęcia funkcji i różnych jej własności. Poniżej przedstawimy dwa przykłady.

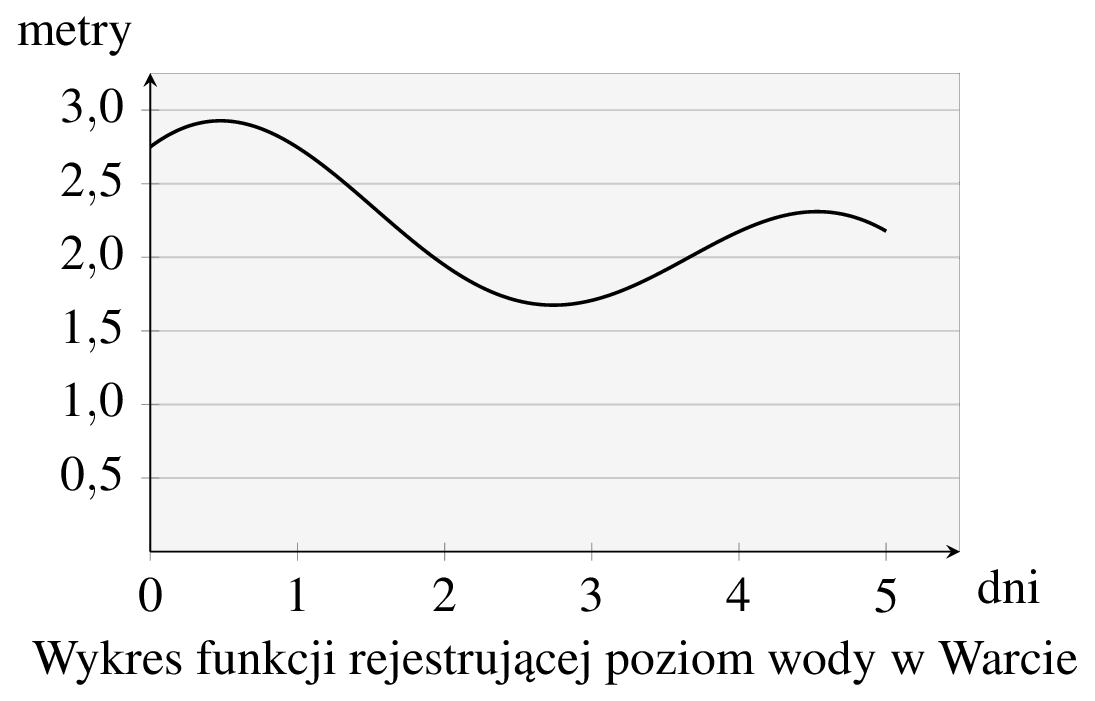
Przypuśćmy, że chcielibyśmy opisać zmianę poziomu wody w Warcie, obserwowaną w jakimś ustalonym punkcie (na przykład na przęśle mostu św. Rocha w Poznaniu). Mamy do dyspozycji urządzenie, które poziom wody rejestruje w czasie rzeczywistym. Gdybyśmy chcieli zaprezentować zmianę poziomu wody w czasie trwającej pięć dni obserwacji, to mogłoby wyglądać to na przykład tak, jak na poniższej ilustracji.

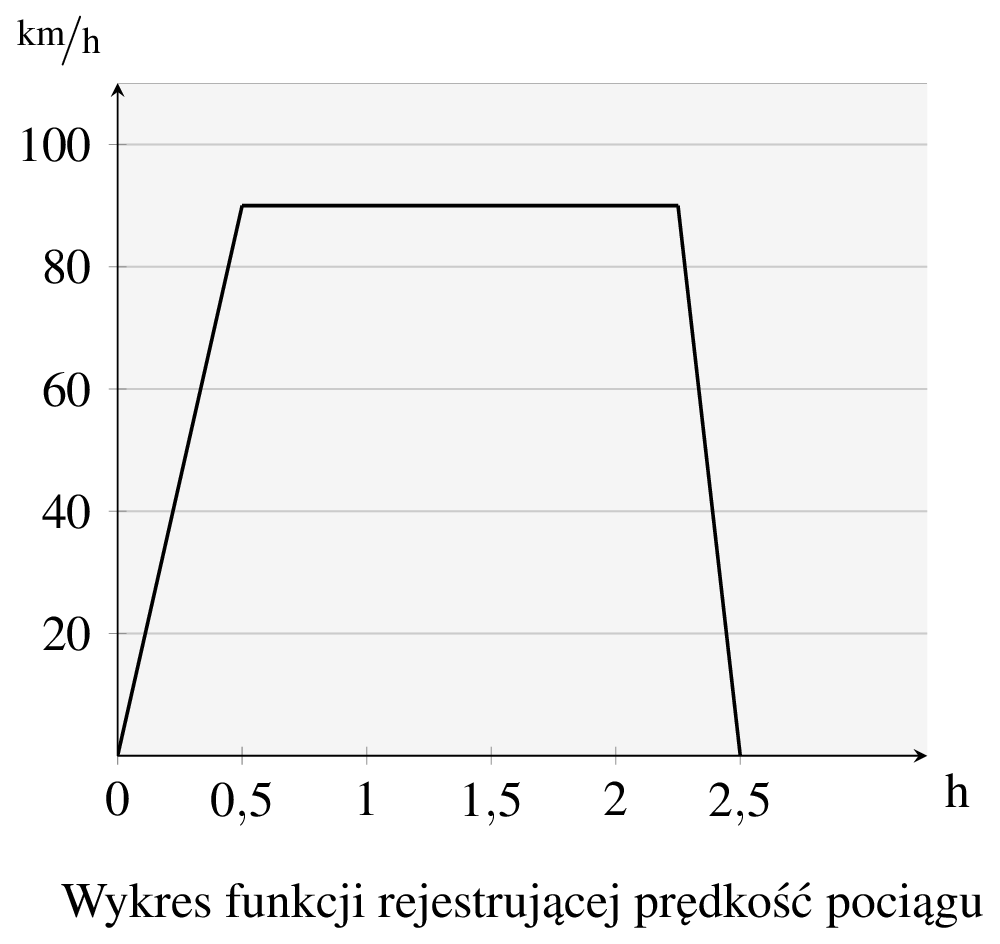
Wyobraźmy sobie, że w pociągu którym się poruszamy, zamontowano urządzenie rejestrujące prędkość. Wówczas zapis dwuipółgodzinnej podróży mógłby wyglądać jak na poniższym rysunku.

Zauważmy, że w obu przypadkach otrzymujemy wykres pewnych funkcji. Przypatrzmy się im jeszcze przez chwilę. Zauważmy, że nieduża zmiana argumentu (czasu) powoduje niedużą zmianę wartości funkcji (odpowiednio, poziom wody i prędkość). Okazuje się, że taką naturę ma zdecydowana większość zjawisk w przyrodzie. Matematycy funkcje mające taką własność nazywają funkcjami ciągłymi. Nie jest naszym celem w sposób formalny i matematycznie ścisły ciągłość definiować. Zadowolimy się w to miejsce intuicją i kilkoma, mamy nadzieję, sugestywnymi rysunkami³. O funkcji powiemy zatem, że jest ciągłą, jeśli „bliskie” sobie punkty dziedziny odwzorowuje na „bliskie” sobie wartości funkcji. Dopowiedzmy, że znana być może czytelnikom definicja ciągłości według Cauchy’ego (ta, w której korzysta się zwykle z symboli \(\varepsilon\) i \(\delta\)), nadaje ilościowego charakteru powyższym słowom „bliskie”.⁴

Poniżej przedstawmy kilka przykładów funkcji ciągłych.

• Każdy wielomian jest funkcją ciągłą

• Funkcje trygonometryczne są funkcjami ciągłymi

• Funkcje wymierne są odwzorowaniami ciągłymi.

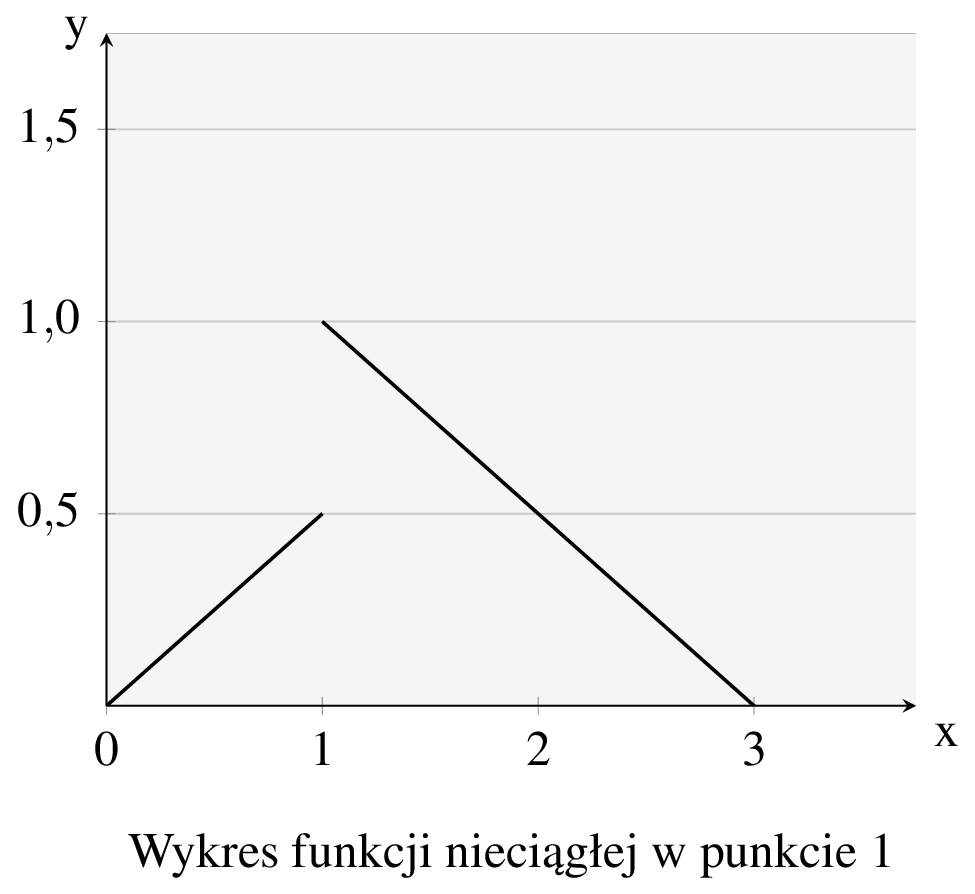
Oczywiście nie wszystkie funkcje są ciągłe. Poniżej prezentujemy wykres funkcji, która nie jest ciągła w punkcie \(1\).

O stycznych do wykresu funkcji

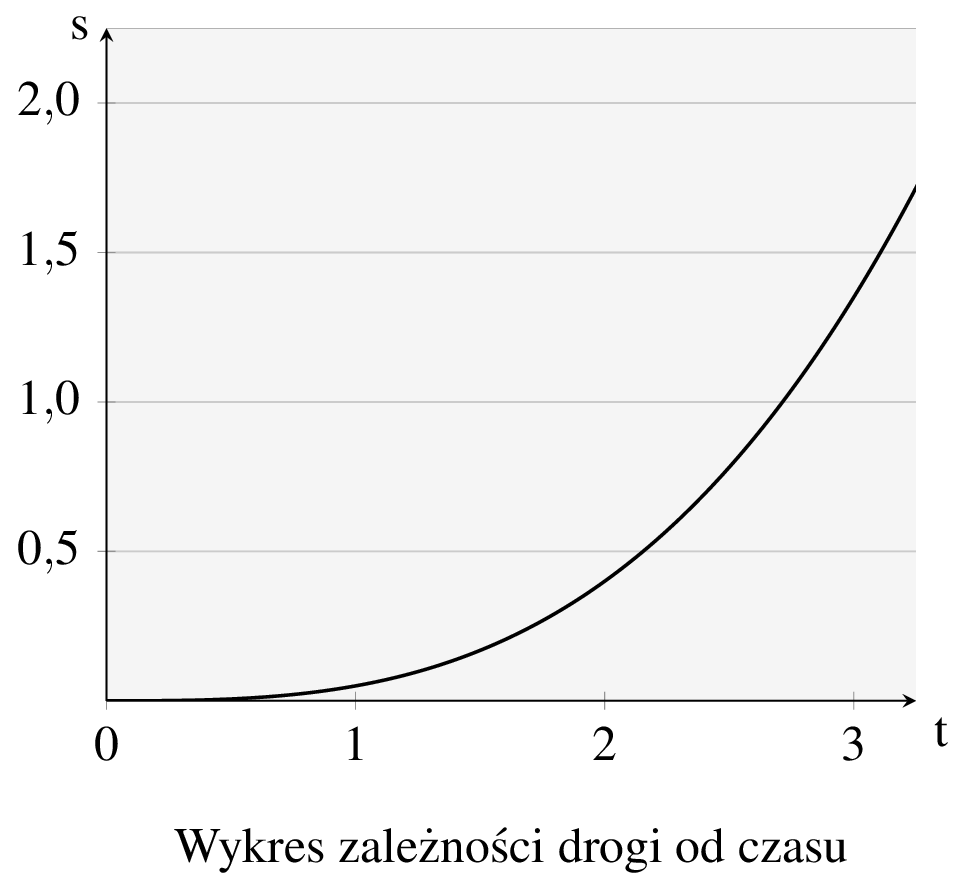
Jesteśmy zainteresowani możliwością rysowania stycznych do wykresów funkcji. Taka umiejętność bywa bowiem bardzo przydatna. Wyobraźmy sobie na przykład, że dysponujemy wykresem drogi (funkcji \(s\) zmiennej czasu \(t\)) poruszającego się jakiegoś obiektu. Jaka fizyczną wielkość da się odczytać, rysując styczną do wykresu funkcji w danym punkcie?

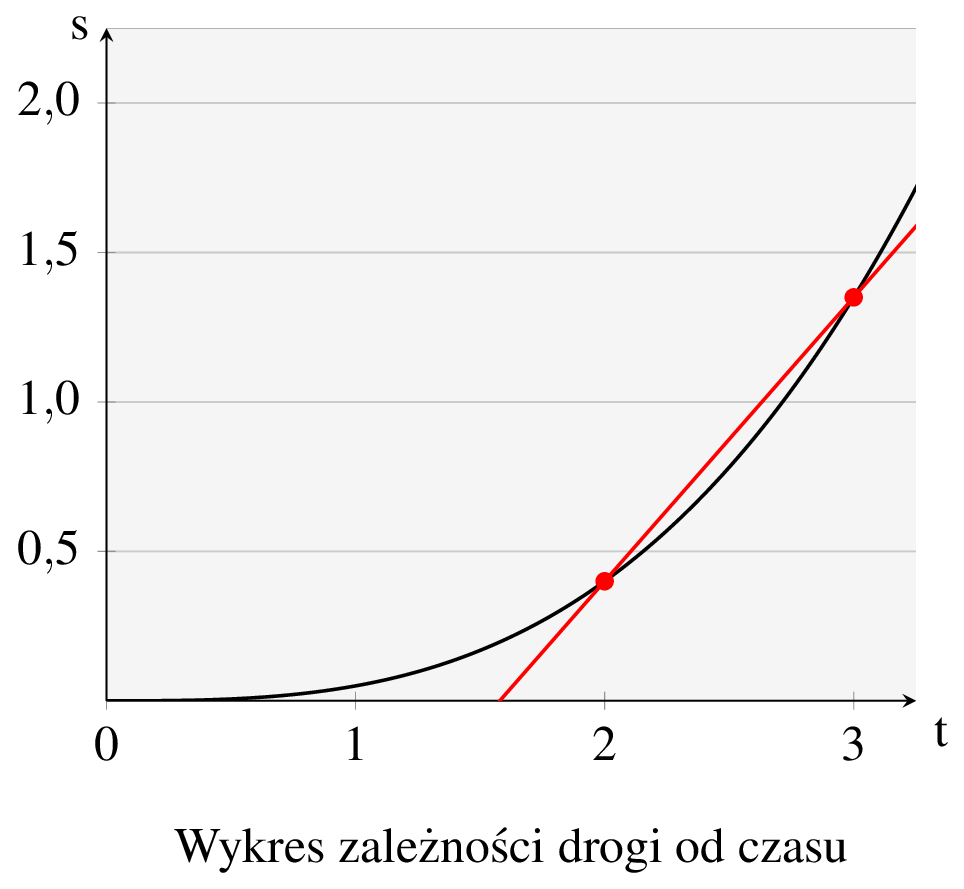
Zacznijmy od poniższego przykładu. Za chwilę zrozumiemy, mam nadzieję, czym jest styczna do wykresu funkcji \(s\) w punkcie \(t_0\). Zamiast rysować od razu styczną, narysujmy na początek prostą (na poniższym rysunku oznaczoną kolorem czerwonym) przechodzącą przez interesujący nas punkt \(t_0\) oraz jakiś inny punkt \(t_1\).

Zauważmy teraz, że iloraz zmiany drogi \(s(t_1)-s(t_0)\) do przyrostu czasu \(t_1-t_0\)
\begin{equation}\label{diff}
\frac{s(t_1)-s(t_0)}{t_1-t_0}
\end{equation}
jest prędkością średnią, z jaką poruszał się obiekt w rozważanym przedziale czasu.

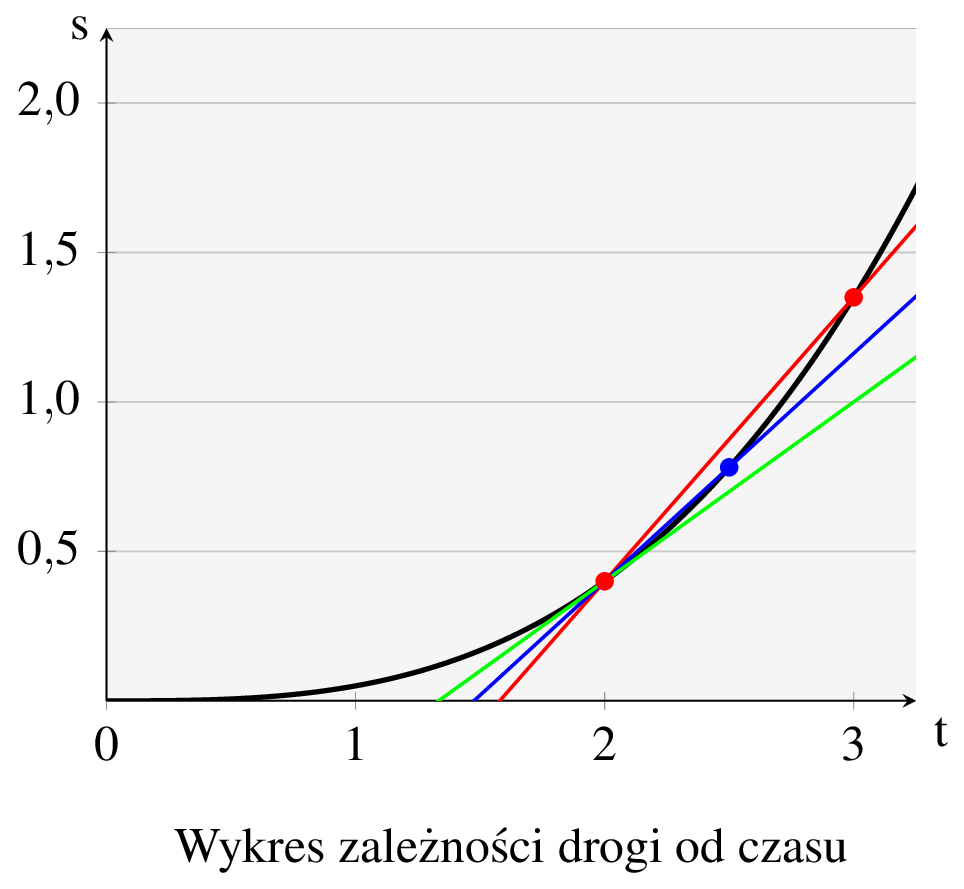
Zastanówmy się co się stanie, gdy punkt \(t_1\) będzie coraz bliższy punktowi \(t_0\).⁵ Wówczas proste przechodzące przez punkt \(t_0\) i kolejne punkty \(t_1\) będą coraz bardziej zbliżać się do… stycznej do funkcji \(s\) w punkcie \(t_0\) (na poniższym rysunku oznaczoną kolorem zielonym), co fizycy nazywają prędkością chwilową.⁶ Ilustruje to poniższy rysunek.

Poniżej można samodzielnie przetestować powyższe rozumowanie.

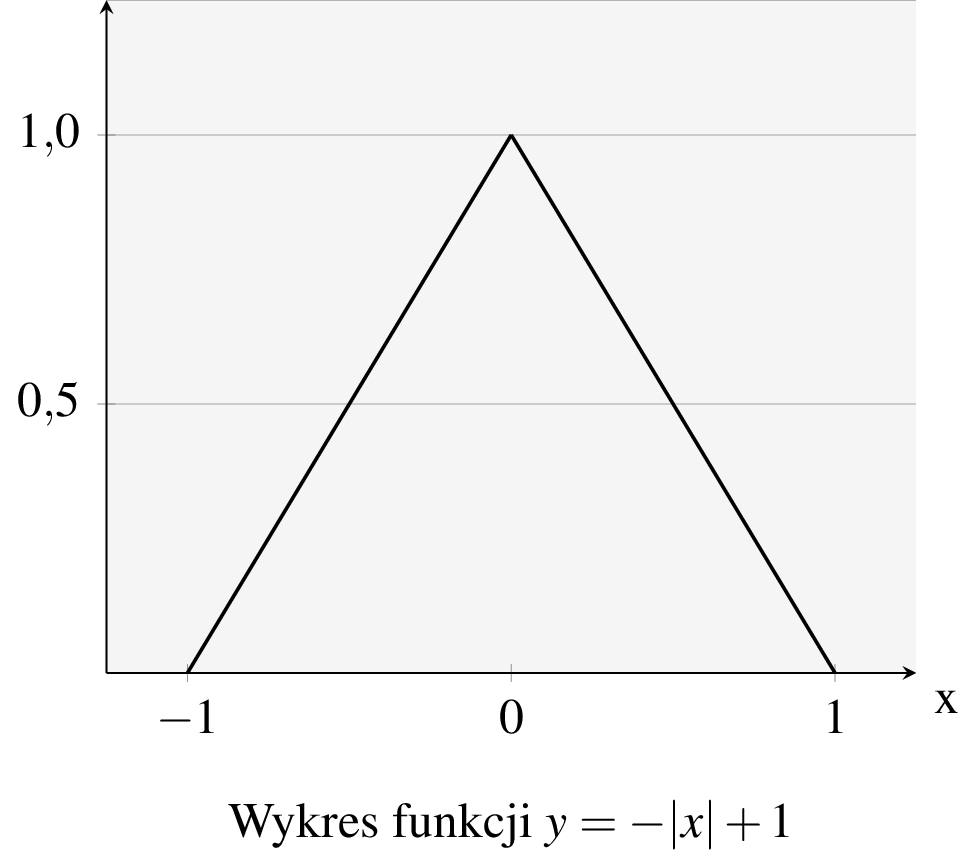
Powyższe rozumowanie, choć zapewne dość sugestywne, zawiera jednak pewną znaczącą nieścisłość. Nie jest przecież powiedziane, że dla danej funkcji w każdym punkcie da się narysować styczną. Rozważmy funkcję \(g\colon \mathbb{R}\to\mathbb{R}\) daną wzorem \(g(x)=-|x|+1\). Jej wykres prezentujemy poniżej.

Zauważmy, że dla argumentu \(x=0\) funkcja \(g\) nie posiada stycznej! Dodatkowo, odnotujmy, że w tym samym punkcie \(g\) jest ciągłą.

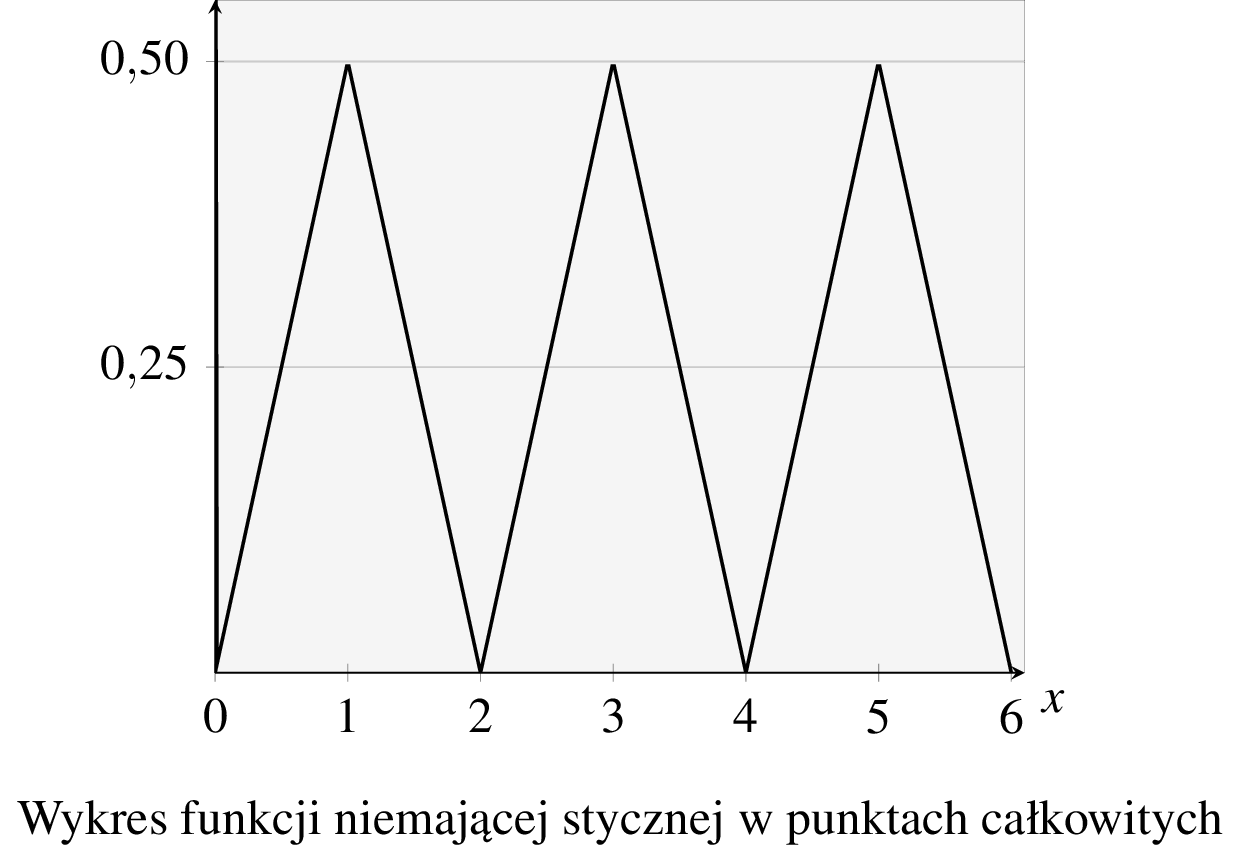
Mamy zatem pierwszy przykład funkcji ciągłej, dla której istnieje punkt, w którym funkcja ta nie ma stycznej. Dość łatwo jest wyobrazić sobie funkcję, która takich punktów ma dwa, trzy…, a nawet nieskończoną ilość! Istotnie, poniżej prezentujemy wykres funkcji, której każdy argument będący liczbą całkowitą ma rozważaną własność.

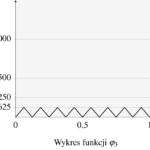
Ponieważ w dalszej części będziemy z tej funkcji robić użytek, powiedzmy jak można ją zdefiniować. Niech \(\varphi\colon \mathbb{R}\to \mathbb{R}\) będzie funkcją, której wartość w punkcie \(x\) jest odległością od najbliższej liczby całkowitej.⁷ Na powyższym rysunku znajduje się wykres funkcji \(y=\varphi(2x)\), \(x\in\mathbb{R}\).

W kolejnym paragrafie prezentujemy funkcję ciągłą na przedziale \([0,1]\), która nie ma stycznej w każdym punkcie swojej dziedziny!

Funkcja Takagiego

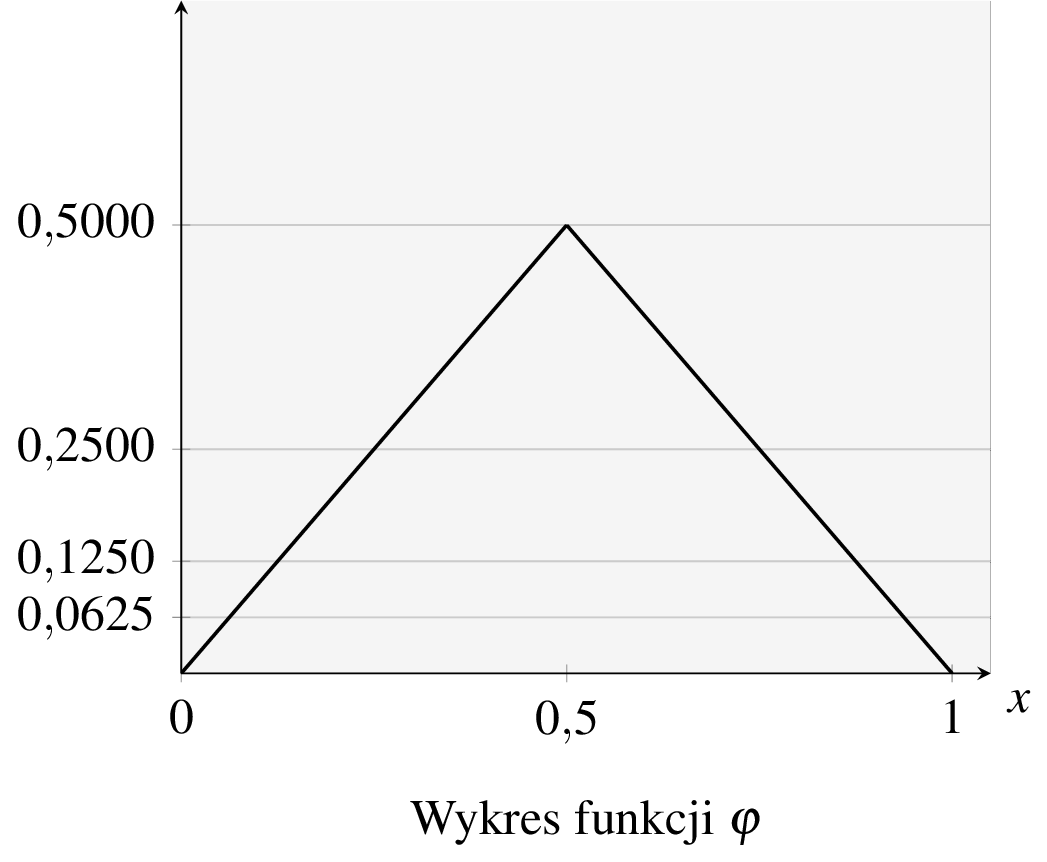
Omówimy konstrukcję funkcji Takagiego. Idea konstrukcji tej funkcji polega ogólnie na tym, by przeprowadzić pewną procedurę zagęszczania ostrzy zmodyfikowanej funkcji „wartość bezwzględna”. Zaczniemy od znanej nam już funkcji \(\varphi\), tym razem określonej na odcinku \([0,1]\). Jej wykres znajduje się poniżej.

Z pomocą funkcji \(\varphi\) określimy inne funkcje, nazywane funkcjami \(\varphi_n\colon [0,1]\to\mathbb{R}\) (\(n=0,1\dots\)), wzorami
\begin{equation*}
\varphi_n(x)=\frac{\varphi(2^n x)}{2^n},\quad x\in [0,1],\ n=0,1\dots.
\end{equation*}
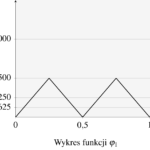
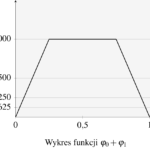
Zauważmy, że jeśli \(n=0\), to \(\varphi_0=\varphi\). Ponadto, poniżej prezentujemy kilka wykresów funkcji \(\varphi_n\) (dla \(n=1,2,3\)).

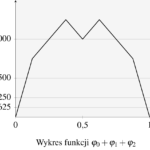
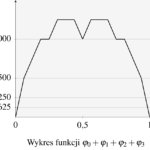
Dodajmy teraz do siebie kolejne funkcje \(\varphi_n\). Wykresy funkcji \(\varphi_0+\varphi_1\), \(\varphi_0+\varphi_1+\varphi_2\), \(\varphi_0+\varphi_1+\varphi_2+\varphi_3\) i \(\varphi_0+\varphi_1+\varphi_2+\varphi_3+\varphi_4\) odpowiednio prezentujemy poniżej.

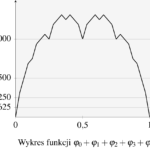
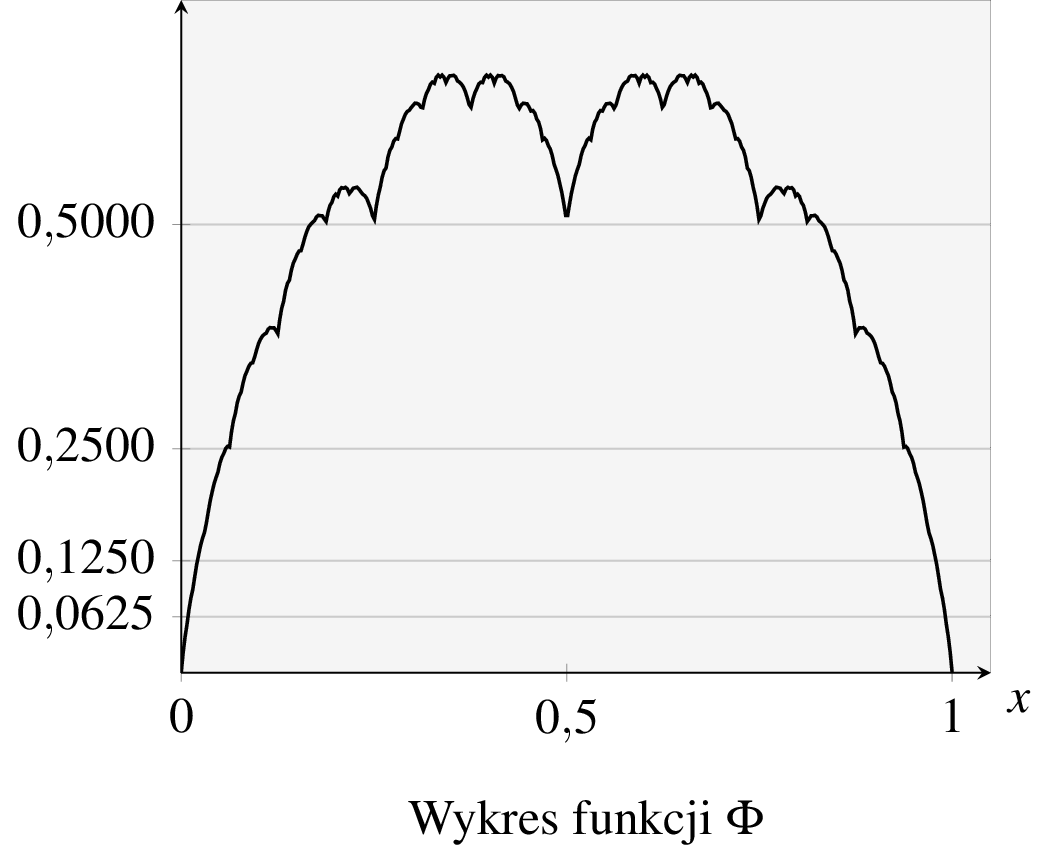
Funkcję Takagiego \(\Phi\colon [0,1]\to\mathbb{R}\) zdefiniujemy następująco:
\begin{equation*}
\Phi(x)=\varphi_0(x)+\varphi_1(x)+\varphi_2(x)+\varphi_3(x)+\dots,\quad x\in[0,1].
\end{equation*}
Wykres funkcji Takagiego znajduje się poniżej.

Uzasadnienie

W niniejszym paragrafie opowiemy (bez wchodzenia jednak w szczegóły) dlaczego funkcja \(\Phi\) jest ciągła na odcinku \([0,1]\) oraz dlaczego nie można narysować do niej stycznej w żadnym punkcie dziedziny. Ten fragment tekstu można pominąć, przechodząc od razu do ostatnich części artykułu.

Po pierwsze, funkcja \(\Phi\) jest ciągła. Ten fakt wynika od razu ze znanego twierdzenia Weierstrassa o majorancie, z którego można wywnioskować, że szereg definiujący funkcję \(\Phi\) jest zbieżny jednostajnie⁸ oraz z faktu, że funkcja będąca sumą zbieżnego jednostajnie szeregu funkcji ciągłych jest funkcją ciągłą.

Uzasadnienie, że \(\Phi\) faktycznie nie ma pochodnej jest bardziej skomplikowane. Przede wszystkim opiera się na poniższym lemacie

Lemat.
Niech \(a<a_n<x<b_n<b, n=1,2,\dots\) i załóżmy, że ciągi \(\{ a_n\}_{n\in\mathbb{N}}\) oraz \(\{ b_n \}_{n\in\mathbb{N}}\) są zbieżne do \(x\). Jeżeli \(f\colon [a,b]\to\mathbb{R}\) jest funkcją ciągłą i różniczkowalną, wówczas
\begin{equation*}
\lim_{n\to\infty}\frac{f(b_n)-f(a_n)}{b_n-a_n}=f'(x).
\end{equation*}

Uzasadnienie przeprowadzimy metodą „nie wprost”⁹. Wybierzmy punkt \(x\in(0,1)\).¹⁰ Istnieją takie elementy \(u_n=\frac{i-1}{2^n}\) oraz \(v_n=\frac{i}{2^n}\) przedziału \((0,1)\), że \(u_n\le x<v_n\). Ponadto z konstrukcji funkcji \(\varphi_n\) wynika, że dla \(k\ge n\), mamy
\begin{align*}
\varphi_k(u_n)&=\frac{\varphi(2^k\frac{i-1}{2^n})}{2^k}=0\\
\varphi_k(v_n)&=\frac{\varphi(2^k\frac{i}{2^n})}{2^k}=0
\end{align*}
Jeśli natomiast \(k\le n-1\), to \(\varphi_k\) są linowe na \([u_n,v_n]\). Załóżmy, że w punkcie \(x\) istnieje pochodna funkcji \(\Phi\) i rozważmy iloraz
\begin{equation*}
\frac{\Phi(v_n)-\Phi(u_n)}{v_n-u_n}=\sum_{k=0}^{\infty}\frac{\varphi_k(v_n)-\varphi_k(u_n)}{v_n-u_n}.
\end{equation*}
Z powyższego wynika, że
\begin{equation*}
\frac{\Phi(v_n)-\Phi(u_n)}{v_n-u_n}=\sum_{k=0}^{n-1}\frac{\varphi(v_n)-\varphi_k(u_n)}{v_n-u_n}=\sum_{k=0}^{n-1}E_k
\end{equation*}
przy czym \(E_k=1\) lub \(E_k=-1\). Zatem granica \(\lim_{n\to\infty}\frac{\Phi(v_n)-\Phi(u_n)}{v_n-u_n}\) nie istnieje, gdyż szereg \(\sum_{k=0}^{\infty} E_k\) nie jest zbieżny (wyraz ogólny tego szeregu nie dąży do zera). Wystarczy teraz skorzystać z powyższego lematu.

Zamiast zakończenia

Nasza opowieść o funkcjach, ciągłości i możliwości rysowania stycznych zbliżą się już ku końcowi. Bardziej wprawionemu w matematyczny żargon czytelnikowi wyjaśnijmy, że powyższe rozważania można by ująć tak: istnieje funkcja ciągła na odcinku \([0,1]\), które nie ma pochodnej w żadnym punkcie tego odcinka. Ten fakt uzupełnia znane twierdzenie z analizy matematycznej, które orzeka, że jeśli funkcja ma w jakimś punkcie swojej dziedziny pochodną, to jest w tym punkcie ciągła. Mówiąc „po naszemu” — w punktach, w których można narysować styczną do wykresu funkcji, musi ona być ciągła.

Na koniec zadajmy pytanie o to, których funkcji jest więcej: funkcji ciągłych mających pochodną w każdym punkcie dziedziny, czy funkcji ciągłych, które pochodnej nie mają w żadnym punkcie dziedziny.¹¹ Odpowiedź na to pytanie może być zaskakująca, bo przecież nasze dotychczasowe doświadczenie sugerowałoby¹², że więcej jest funkcji mających pochodną. A jednak, znacznie więcej jest funkcji, które pochodnej nie mają w żadnym punkcie dziedziny. Wynika to z twierdzenia udowodnionego przez polskiego matematyka Stefana Banacha na początku XX wieku. Dowód tego faktu¹³, a nawet jego sformułowanie, wykracza poza ramy niniejszego artykułu, pozostawmy je więc na inną okazję.

Wyjaśnijmy wreszcie tytuł niniejszego artykułu. Otóż jak widzieliśmy powyżej, prędkość jest styczną do funkcji drogi. Zauważmy dodatkowo, że współczynnik nachylenia stycznej wskazuje na kierunek poruszania się (gdy współczynnik dodatni, ciało porusza się do przodu, gdy ujemny — do tyłu). W punktach, w których znajdowały się ostrza funkcji, funkcja zmieniała kierunek (na lewo od punktu ciało poruszało się do przodu, na prawo — do tyłu). Omawiana w tekście funkcja Takagiego to takie odwzorowanie, które — mówiąc bardzo oględnie — w każdym punkcie swojej dziedziny zmienia kierunek (porusza się więc „tam i z powrotem”).¹⁴

Teiji Takagi

Teiji Takagi¹⁵ (1875–1960) był japońskim matematykiem, specjalizującym się w algebraicznej teorii liczb. Dowód na istnienie funkcji ciągłej na odcinku, która nie ma pochodnej w żadnym punkcie dziedziny zaprezentował w 1901 roku. Matematyką zaczął interesować się w szkole średniej, studiował na uniwersytecie w Tokio, a następnie w Getyndze w Niemczech. W czasie drugiej wojny światowej pracował nad udoskonaleniem szyfrów, którymi posługiwało się japońskie wojsko. Jest autorem wielu popularnych w Japonii podręczników do nauki matematyki.

Przypisy

1. Jeśli dla Ciebie, Czytelniku, wcale nie jest to w tej chwili łatwe, proszę o chwilę cierpliwości — kilka akapitów niżej znajdziesz taką funkcję, a nawet jej wykres.
2. To bardzo sympatyczne, że wiele obiektów lub twierdzeń matematycznych nosi nazwy związane ze swoimi odkrywcami. Dzięki temu uświadamiamy sobie ponadczasowość matematyki i jej uniwersalność. To jeden z argumentów by matematyki się uczyć, a nawet twórczo ją rozwijać! Być w może w przyszłości będziemy pisać o twierdzeniach nazywanych Twoim nazwiskiem?
3. Jeśli jednak chciałbyś zobaczyć w jaki sposób matematycy definiują ciągłość funkcji,
   zachęcamy, być sięgnął do tego tekstu.
4. Autor niniejszego tekstu uważa przy tym, że fakt nadawania ilościowego charakteru własnościom obiektów jest jednym z najważniejszych osiągnięć matematyki.
5. Ci, którzy znają pojęcie funkcji wiedzą — jak sądzę — że pytamy tutaj o granicę ilorazu \eqref{diff} gdy \(t_1\to t_0\).
6. Omawiana właśnie własność „posiadania stycznej w punkcie” jest mało formalnym wyrażeniem faktu, że funkcja posiada pochodną w punkcie. Nie chcemy jednak czytelnikowi prezentować detali związanych z pochodną (w szczególności definicji), żeby nie utrudniać odbioru istoty tego tekstu. Ufamy, że zainteresowany i dociekliwy czytelnik bez trudu znajdzie definicje nieznanych sobie pojęć (pochodna, granica funkcji).
7. Czytelnik jest usilnie proszony, by w tym miejscu policzył wartość funkcji \(\varphi\) w kilku wybranych punktach, ale niekoniecznie będących liczbami całkowitymi.
8. Zauważmy, że
   \[
   |\varphi_n(x)|=\left|\frac{\varphi(2^n x)}{2^n}\right|\leq \frac{1}{2^n},\quad x\in [0,1],
   \]
   a więc składniki szeregu
   \[
   \sum_{n=0}^\infty \varphi_n(x)
   \]
   mają majorantę, która jest sumowalna, gdyż
   \[
   \sum_{n=0}^\infty \frac{1}{2^n}=2.
   \]
9. Odsyłamy czytelnika do tekstu wprowadzającego w różnorodne metody dowodzenia.
10. Uzasadnienie w przypadku końców odcinka przeprowadza się podobnie.
11. Czy można w ogóle pytać o to, których funkcji jest więcej? Tak! Choć oczywiście trzeba wyjaśnić, co rozumie się pod pojęciem „jest więcej”.
12. Przypomnijmy, że w szkole zajmujemy się przeważnie funkcjami różniczkowalnymi, nawet jeśli nie wspomina się o tym zbyt często.
13. Twierdzenie Banacha jest wielkim osiągnięciem powstałej na początku XX wieku analizy funkcjonalnej — teorii matematycznej zajmującej się badaniem przestrzeni funkcji. Zaintersowany czytelnik być może chciałby przeczytać artykuł o przestrzeni
    funkcji ciągłych.
14. Jak czytelnik zapewne zauważył, tytuł oddaje również fascynację autora niniejszego tekstu pisarstwem Johna Ronalda Reuela Tolkiena.
15. O Teijim Takagim można poczytać m.in. w Wikipedii.

---

Ten artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu „Potęga matematyki”.