Trzy prawa Keplera
W 1609 roku Jan Kepler publikuje jedno z najważniejszych dzieł naukowych pierwszej połowy XVII wieku, Astronomia ~Nova, gdzie formułuje tzw. dwa pierwsze prawa Keplera opisujące w jaki sposób planety poruszają się w Układzie Słonecznym. W 1619 publikuje on pracę Harmonices~Mundi, gdzie formułuje on prawo trzecie.
W Układzie Słonecznym, każda planeta porusza się po torze w kształcie elipsy, w której jednym z ognisk jest Słońce,
W równych odstępach czasu promień wodzący planety poprowadzony od Słońca zakreśla równe pola,
Stosunek kwadratu okresu obiegu planety wokół Słońca do sześcianu wielkiej półosi orbity jest stały dla wszystkich planet w Układzie Słonecznym.
Przeanalizujmy co tak naprawdę mówią nam te prawa, które stały się podstawą fizyki oraz astronomii w kolejnych wiekach.
Elipsa
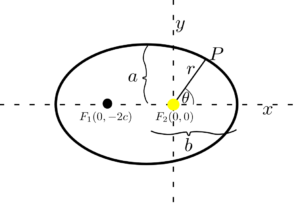
Definicja. Elipsą nazywamy zbiór wszystkich punktów P spełniających warunek
$$|PF_1|+|PF_2|=2a,$$ gdzie F_1, F_2 są ustalonymi punktami (tzw. ogniskami elipsy), natomiast $a>0$ jest ustaloną stałą.
Inaczej, elipsa to zbiór punktów, których suma odległości od dwóch ognisk jest taka sama. Przyjmijmy teraz, że punkty $F_1, F_2$ leżą na osi $OX$ i mają współrzędne $F_1=(0,-2c)$ oraz $F_2=(0,0).$ Możemy uzyskać wówczas analityczną postać elipsy
$$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1,$$
gdzie związek pomiędzy $a$ oraz $b$ jest następujący
$$c = \sqrt{a^2 – b^2}.$$
Rozważmy teraz położenie punktu $P=(x,y)$ na elipsie, wykorzystując tzw. układ współrzędnych biegunowych, gdzie zamiast informacji o koordynatach na osi, będziemy mówić o odległości punktu od jednej z ognisk (w naszym przypadku niech to będzie punkt $F_2$) oraz o kącie $\theta$ jaki tworzy prosta $F_2P$ z osią $OX$. Wówczas, każdy punkt możemy przedstawić następująco
$$
\left\{
\begin{array}{c}
x=r \cos \theta\\
y=r \sin \theta
\end{array}
\right.
$$
Możemy wówczas uzyskać postać biegunową elipsy
$$r^2=\dfrac{a^2b^2}{a^2-c cos^2 \theta}.$$
I prawo Keplera
Analizując rysunek przedstawiający elipsę, umieszczając Słońce w jednym z ognisk, możemy zwizualizować trajektorię poruszania się dowolnej planety w Układzie Słonecznym. Pierwsze prawo Keplera pozwala nam uzyskać wiele informacji odnośnie charakterystyki obiegu planety – np. przybliżoną długość trasy jaką przebywa planeta w ciągu pełnego okrążenia wokół Słońca, znając odległość pomiędzy nimi.
II prawo Keplera
Skoro w równych odstępach czasu planeta zakreśla takie same pole, a porusza się po elipsie, musi to oznaczać, że prędkość jej poruszania musi być większa w przypadku dużej odległości od Słońca oraz planeta zwalnia, gdy przybliża się do niego. Spróbujmy dowieść prawdziwości tego prawa – rozważmy postać elipsy zdefiniowaną w pierwszym punkcie
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$$
Wykorzystując odpowiednie zależności związane z własnościami elipsy, jesteśmy w stanie obliczyć odległość ogniska od środka elipsy
$$c=ea,$$
długość krótszej osi
$$b=\sqrt{a^2-c^2},$$
oraz pole powierzchni elipsy
$$A=\pi ab.$$
Niech teraz d$t$ oznacza bardzo mały przyrost czasu, w którym planeta okrążająca Słońce przemierza drogę po elipsie, a d$\theta$ oznacza bardzo mały przyrost kąta $\theta$. Wielkość pola jakie planeta „zakreśliła” promieniem wodzącym od Słońca, możemy w przybliżeniu wyliczyć z pola trójkąta o podstawie $r $ oraz wysokości $r\text{d}\theta$, gdzie wysokość przybliżamy za pomocą długości łuku, korzystając z zależności $\frac{l}{2 \pi r}=\frac{\text{d}\theta}{2 \pi}$. Zatem pole to wynosi
$$A=\frac{r^2\text{d}\theta}{2}.$$
Zastanówmy się teraz, ile pola „zakreślimy” w bardzo małym odstępie czasu, d$t$, w trakcie okrążania Słońca po elipsie. Pytamy się wówczas tak naprawdę o prędkość polową, która jest pochodną funkcji pola $A$ względem czasu $t$
$$\frac{\text{d}A}{\text{d}t}=\frac{r^2}{2}\frac{\text{d}\theta}{dt}.$$
Mając dany czas jaki ciało potrzebuje na wykonanie pełnego obiegu wokół słońca (tzw. okres orbitalny) $P$, mamy następującą równość
$$P\frac{r^2}{2}\frac{\text{d}\theta}{\text{d}t}=\pi ab.$$
Zatem
$$\frac{\text{d}A}{\text{d}t}=\frac{r^2}{2}\frac{\text{d}\theta}{dt}=\frac{\pi ab}{P}=const.$$
Stąd otrzymujemy, iż promień wodzący zakreśla stałe pole w równych odstępach czasu.
Poniższa animacja obrazuje drugie prawo Keplera. Przesuwając wskaźnik „długość okna” ustalamy wielkość zakreślonego pola. Zmieniając wartość mimośrodu możemy sterować wielkością spłaszczenia elipsy.
III prawo Keplera
Wyobraźmy sobie dowolną planetę w Układzie Słonecznym krążącą wokół Słońca. Słońce przyciągą ją pod wpływem siły grawitacji wyrażonej wzorem:
$$F_{graw} = G\frac{Mm}{R^2},$$
Gdzie:
G– stała grawitacyjna,
M– masa Słońca,
m– masa planety,
R– odległość planety od Słońca.
Oczywiście gdyby siła grawitacyjna była niezrównoważona, wtedy planeta „spadłaby” na Słońce. Siłą równoważącą siłę grawitacji jest zatem siła odśrodkowa w ruchu po okręgu planety wokół Słońca (dla uproszczenia rachunków przyjmijmy, że orbita jest okręgiem, a nie elipsą). Siła odśrodkowa wyraża się wzorem
$$F_{odsr}=m\omega^2R,$$
Gdzie $\omega$ to prędość w ruchu po okręgu. Spełniona jest pierwsza zasada dynamiki Newtona – siła grawitacyjna i odśrodkowa równoważą się:
$$F_{graw} = F_{odsr}.$$
Podstawiając wartości sił do równości dostajemy
$$G\frac{Mm}{R^2} = m\omega^2R.$$
Skracając $m$ i dzieląc obustronnie przez $R$ mamy
$$G\frac{M}{R^3} = \omega^2.$$
Podstawiając $\omega=\frac{2\pi}{T}$ ($T$ to okres obiegu planety) otrzymujemy
$$G\frac{M}{R^3} = \frac{4\pi^2}{T^2}.$$
Mnożąc teraz równanie obustronnie przez $R^3$ i dzieląc przez $4\pi^2$ uzyskujemy
$$G\frac{M}{4\pi^2} = \frac{R^3}{T^2}.$$
Zauważmy teraz następującą rzecz- lewa strona równości nie zależy od masy naszej planety, ani promienia jej orbity. Jest zatem prawdziwa dla dowolnej planety w Układzie Słonecznym! Jaki z tego wniosek? Dla dowolnych dwóch planet w Układzie Słonecznym mamy
$$\frac{R_1^3}{T_1^2}=\frac{R_2^3}{T_2^2}=\frac{GM}{4\pi^2},$$
gdzie:
T_1– czas obiegu pierwszej planety,
T_2– czas obiegu drugiej planety,
R_1– promień orbity pierwszej planety,
R_2– promień orbity drugiej planety.
Ta zależność znana jest jako Trzecie prawo Keplera. Zatem im większa jest odległość planety od Słońca, tym dłuższy jest jej okres. W rzeczywistości jednak orbity planet są eliptyczne (wtedy w powyższej równości R_1 i R_2 wyrażają wielkie półosie elipsy).
Dla ilustracji trzeciego prawa Keplera została przygotowana poniższa symulacja. Pierwsza planeta porusza się po elipsie o wielkiej półosi równej 200 jednostek. Wielką półoś drugiej planety możemy wybrać sami za pomocą suwaka. Następnie przesuwając czas obserwujemy, jak kształtują się orbity naszych planet.
Wykorzystując Trzecie prawo Kepplera można na przykład obliczyć masę Słońca, jeżeli znamy okres obiegu Ziemi wokół Słońca (1 rok) oraz wielką półoś jej orbity. Co więcej znając stałą $\frac{GM}{4\pi^2}$, można obliczyć wielką półoś orbity dowolnej planety mając jedynie okres jej obiegu.
