„Niech nikt nie wkracza tutaj, kto nie zna geometrii.”

NAPIS PRZY WEJŚCIU DO AKADEMII PLATOŃSKIEJ

O BRYŁACH PLATOŃSKICH

Poniżej przedstawimy rozumowanie, które pozwala wykazać, że istnieje tylko pięć brył foremnych, zwanych też platońskimi (Platon): czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan. Dowód pochodzi z X księgi Euklidesa i jego autorem jest Pitagoras, jak i Teajtet.

Rozumowanie przedstawimy w kilku elementarnych krokach.

KĄTY W WIELOKĄCIE FOREMNYM

Rozważmy wielokąt foremny o $n$ bokach, $n\geq 3$

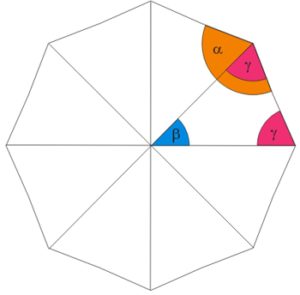
Kąt $\alpha = 2 \cdot \gamma$, więc wzór na sumę kątów $\gamma + \gamma + \beta = 180^{\circ}$ daje $\alpha + \beta = 180^{\circ}$. Zatem $n \cdot \alpha + n \cdot \beta = n \cdot 180^{\circ}$. Wstawiając teraz $n \cdot \beta = 360^{\circ}$ i dzieląc obie strony równości przez $n$, dostajemy

$$\alpha = 180^{\circ} – \frac{360^{\circ}}{n} \ \ \hbox{dla każdego} \ \ n \geq 3.$$

TWIERDZENIE PITAGORASA-TEAJTETA O BRYŁACH FOREMNYCH

Istnieje dokładnie pięć brył foremnych: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan.

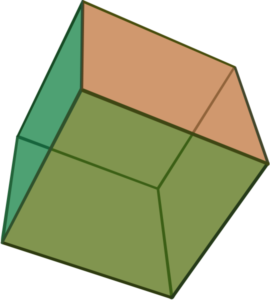
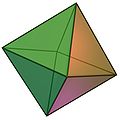
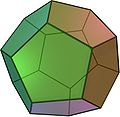
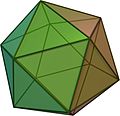
DOWÓD PITAGORASA -TEAJTETA ZAPISANY W „ELEMENTACH” EUKLIDESA

Rozważmy bryłę foremną, której ściany są tym samym $n$-bokiem foremnym, a każdy wierzchołek utworzony jest przez $k$ ścian dla $n \geq 3$ oraz $k \geq 3$. Niech $\alpha$ będzie kątem wewnętrznym zawartym pomiędzy sąsiednimi bokami w $n$-boku foremnym. Wobec tego $\alpha = 180^{\circ} – \frac{360^{\circ}}{n}$, lecz $k \cdot \alpha < 360^{\circ}$, więc $\alpha < 120^{\circ}$, bo $k \geq 3$.

         

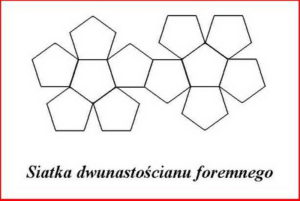
Zatem $180^{\circ} – \frac{360^{\circ}}{n} < 120^{\circ}$, co jest możliwe tylko dla $n = 3$, $4$, $5$.

Skoro $n = 3$, $4$, lub $5$, to ze wzorów

$$\alpha = 180^{\circ} – \frac{360^{\circ}}{n} \ \ \ \hbox{oraz} \ \ k \cdot \alpha < 360^{\circ}$$
wynika, że możliwe są następujące przypadki.
$\bullet$ Dla $n = 3$: $\alpha = 60^{\circ}$, $k = 3$, $4$, $5$.    

$\bullet$ Dla $n = 4$: $\alpha = 90^{\circ}$, $k = 3$. 

$\bullet$ Dla $n = 5$:  $\alpha = 108^{\circ}$,  $k = 3$. 

Podsumowując $(n,k) = (3,3)$, $(3,4)$, $(3,5)$, $(4,3)$, $(5,3)$. $\square$