Zobacz poprzednią część tego artykułu

Ostatni bastion ludzkości

W 1996 roku doszło do niezwykłej konfrontacji − wieloletni mistrz świata w szachach, Garri Kasparow, podjął wyzwanie rzucone przez firmę IBM i stworzony przez nią komputer Deep Blue. Sztuczna inteligencja miała stawić czoła jednemu z największych, a może nawet największemu geniuszowi wszechczasów w szachach. Wszyscy wielcy szachiści tamtych czasów, w tym także Kasparow, byli przekonani, że maszyna − pozbawiona ludzkiej kreatywności − nigdy nie będzie w stanie pokonać człowieka. Tak też się stało − mecz zakończył się wynikiem 4:2 dla Kasparowa.

Po raz pierwszy jednak komputer wygrał wtedy partię z mistrzem świata w szachach, co tylko podgrzało debatę na temat przewagi człowieka nad komputerem. Specjaliści od sztucznej inteligencji z IBM pracowali przez cały rok, dopracowali heurystyki¹ oceny sytuacji na planszy, a także znacząco zwiększyli moc obliczeniową Deep Blue (do 300 milionów analizowanych pozycji szachowych w ciągu sekundy). Deep Blue mógł ponownie stanąć w szranki z arcymistrzem.

Do rewanżu doszło 11 maja 1997 roku. Pierwszą partię wygrał Kasparow, drugą Deep Blue, po czym nastąpiły trzy remisy. W ostatniej, decydującej szóstej partii lepszy okazał się Deep Blue. Najlepszy szachista świata został pokonany przez sztuczną inteligencję.

Jednak siła Deep Blue bardzo mocno opierała się na ogromnej mocy obliczeniowej. Z tego też powodu szacowano, że ostatni bastion ludzkości w grach planszowych, starożytna chińska gra go, w której kombinacji jest więcej niż atomów we wszechświecie, padnie być może ok. 2100 roku. Była to wiara tym silniejsza, że do 2015 roku komputery potrafiły ogrywać w go jedynie amatorów.

Aż przyszedł marzec 2016 roku. Matematyczny geniusz, założyciel firmy DeepMind Technologies² zajmującej się sztuczną inteligencją, Demis Hassabis stworzył z grupą entuzjastów AI³ AlphaGo − sztuczną inteligencję grającą w go, a następnie rzucił wyzwanie wielkiemu mistrzowi tej gry − Lee Sedolowi, którego supremacja w świecie go jest nawet większa niż to było w przypadku Kasparowa w świecie szachów.

Lee Sedol podjął wyzwanie i był absolutnie pewny, że mecz zakończy się jego zwycięstwem 5:0. To, co się jednak wydarzyło, było niezwykłym zaskoczeniem. Pierwsze trzy partie wygrał AlphaGo, w czwartej rozgrywce Lee Sedolowi udało się w końcu odnieść zwycięstwo i gdy wydawało się, że mistrz go uratuje nadzieje na skuteczną rywalizację człowieka z maszyną, AplhaGo, wygrywając ostatnią partię, postawił kropkę nad i. Wynik 4:1 dla AlphaGo.

Niezwykłość tego zwycięstwa polega na tym, że AlphaGo nie był w żaden specjalny sposób przystosowany do gry w go. Mógł nauczyć się dowolnej gry, o ile tylko mógłby ćwiczyć odpowiednio długo. Tak jak Deep Blue, AlphaGo zapoznał się z setkami tysięcy partii, ucząc się, które pozycje prowadziły do zwycięstwa. Jednak później oceny pozycji na planszy uczył się już zupełnie samodzielnie, rozgrywając sam ze sobą tysiące partii. I nauczył się gry w go tak dobrze, że niejednokrotnie komentatorzy z niedowierzaniem patrząc na planszę wypowiadali słowa w stylu „to niemożliwe, tak się przecież nie gra”, „żaden człowiek nie zagrałby takiego ruchu”. Zaś krótko po meczu zaczęto rozumieć i uczyć się nowych technik i nowego stylu gry, jaki wprowadził AlphaGo. Natomiast sam Lee Sedol wyraził uznanie dla intuicji, jaką wykazywał jego przeciwnik. Maszyna nauczyła się posiadać intuicję i ostatecznie zostawiła człowieka w tyle we wszystkich grach planszowych.

Za potęgą AlphaGo stoją tzw. sieci neuronowe − cyfrowa realizacja, a raczej namiastka − ludzkiego mózgu. Pierwsze sieci neuronowe zostały stworzone już w latach pięćdziesiątych XX wieku, jednak dopiero w ostatnich latach wzrost mocy obliczeniowej komputerów oraz dostępność ogromnych zbiorów danych pozwoliły na pełne wykorzystanie ich możliwości. To właśnie one napędzają obecny rozwój sztucznej inteligencji. Dzięki sieciom neuronowym komputery nauczyły się grać w proste gry komputerowe (przykład na poniższym filmie), jeździć samochodem, sterować robotem, przewidywać przyszłość (oczywiście w ograniczonym zakresie, bazując na dostępnych danych), rozpoznawać obiekty na zdjęciach (zaczęło się naturalnie od kotów), czytać z ruchu warg, tworzyć muzykę, a nawet śnić. I już za chwilę dowiecie się, czym są i jak te sieci neuronowe działają.

Sztuczny mózg

Współczesne badania nad ludzkim mózgiem dowodzą, że jest to organ o wiele bardziej skomplikowany, niż wcześniej przypuszczano. Niepodważalne jest jednak, że kluczową rolę w mózgu pełnią neurony, połączenia między nimi (synapsy) oraz przesyłane między nimi sygnały. I taki właśnie uproszczony model został zastosowany w sztucznym mózgu − w sieciach neuronowych.

Tak jak mózg człowieka przetwarza sygnały elektryczne, tak sieci neuronowe przetwarzają liczby. Zasada działania zawsze jest taka sama − sieć neuronowa otrzymuje pewne informacje wejściowe w postaci szeregu liczb, przetwarza je i na końcu zwraca liczbę (lub kilka liczb) będącą wynikiem. Na pierwszy rzut oka może się wydawać, że to nic wielkiego i właściwie trudno byłoby znaleźć zastosowanie dla takiego narzędzia. Okazuje się jednak, że taką sieć neuronową możemy wykorzystać np. do oceny szansy wystąpienia trzęsienia ziemi w danym regionie, przewidywania ruchów cen akcji, oceny pozycji szachowych, czy też przewidywania, ile w przyszłości będzie zarabiał młody człowiek na podstawie jego wyników z matematyki oraz zarobków rodziców. Dla tego ostatniego przykładu za chwilę wspólnie stworzymy sieć neuronową, dzięki czemu dowiemy się, czy lepiej dobrze się uczyć, czy też lepiej po prostu mieć bogatych rodziców. Natomiast jak można by zrealizować pozostałe przykłady, warto zastanowić się samemu. Po przeczytaniu tego artykułu warto także pomyśleć, jakie jeszcze zastosowania sieci neuronowych przychodzą wam do głowy.

Przejdźmy teraz do naszego przykładu. Chcemy, aby stworzona przez nas sieć neuronowa mówiła nam o przyszłych zarobkach, powiedzmy w wieku 30 lat, nastolatków na podstawie ich średniej ocen z matematyki⁴ oraz zarobków ich rodziców. Gotowej sieci będziemy w stanie podać dowolną kombinację średniej i zarobków (np. średnia 4,34, zarobki obojga rodziców 5 tys. zł miesięcznie), a ona zwróci nam przewidywane przyszłe zarobki (przykładowo 4 tys. zł miesięcznie) osoby, o którą pytamy.

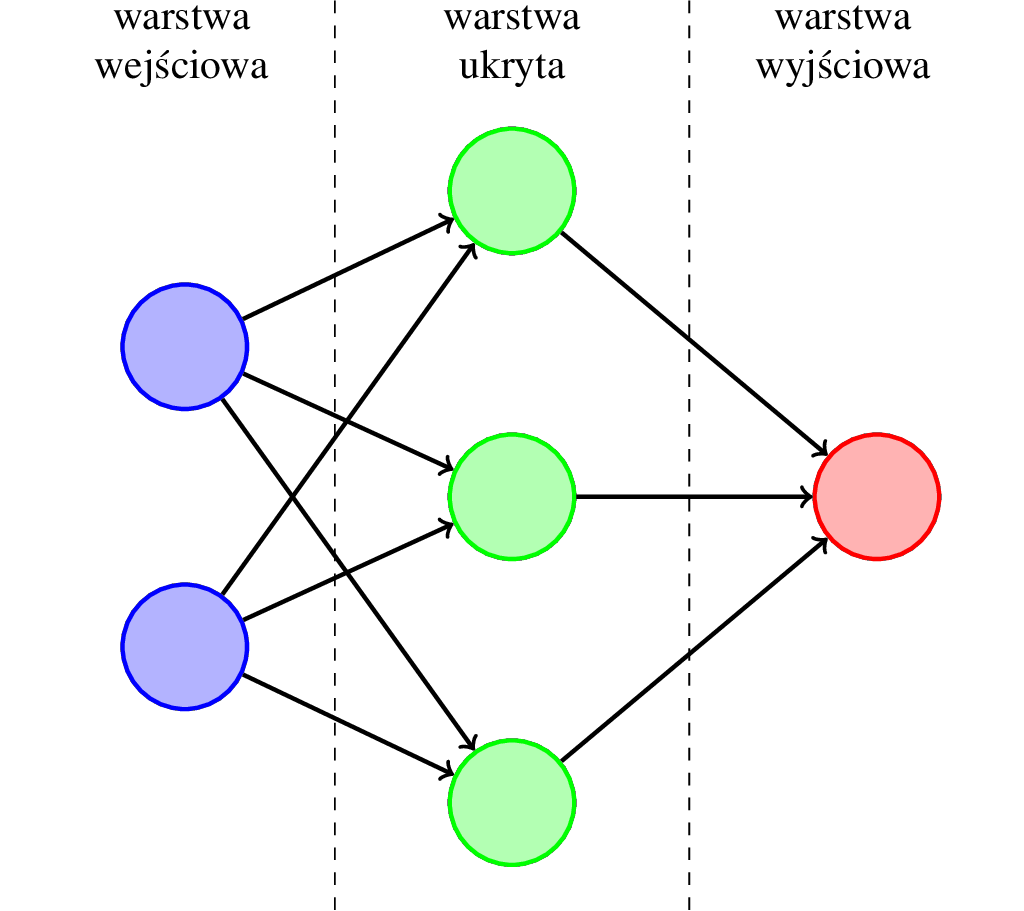
Dla lepszego zrozumienia, jak w praktyce działa sieć neuronowa, posłużymy się poniższym rysunkiem przedstawiającym przykładową sieć.

Jest to sieć składająca się z trzech warstw — warstwy wejściowej składającej się z dwóch neuronów, warstwy ukrytej składającej się z trzech neuronów oraz warstwy wyjściowej składającej się z jednego neuronu.

Dwa neurony w warstwie wejściowej odpowiadają w naszym przykładzie średniej ocen z matematyki oraz zarobkom rodziców.

Warstw ukrytych może być w sieci neuronowej bardzo dużo. Przykładowo, inżynierowie z firmy Microsoft w największej stworzonej na potrzeby rozpoznawania obiektów na zdjęciach sieci neuronowej zastosowali aż 1000 warstw⁵. Nasz problem jest jednak znacznie mniej złożony, wystarczy więc jedna warstwa ukryta.

Neuron w warstwie wyjściowej odpowiada wynikowi, czyli przewidywanym zarobkom.

Działanie takiej sieci polega na przetwarzaniu sygnału w postaci liczb, a zatem na wykonywaniu pewnych obliczeń. W istocie tych obliczeń jest sporo, ponieważ każdy neuron (nie licząc warstwy wejściowej) wykonuje odpowiednie dla niego obliczenia wielkości przekazanych z warstwy po lewej, a wynik przesyła dalej w prawo do wszystkich połączonych z nim neuronów w kolejnej warstwie. Jednak procedura dla każdego neuronu jest identyczna, co powoduje, że główna trudność w zrozumieniu działania sieci neuronowej leży przede wszystkim w natłoku oznaczeń.

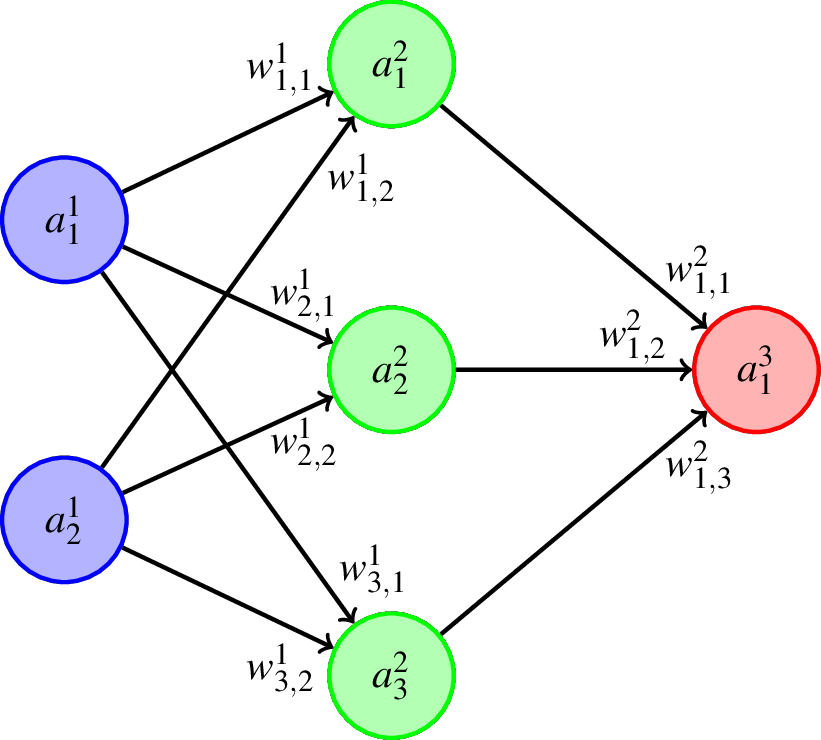
Poniższy rysunek prezentuje kluczowe zmienne występujące w naszej sieci neuronowej.

Ogólne zasady użyte w powyższych oznaczeniach prezentują się następująco:

• literą \(a\) oznaczone są wartości obliczone w poszczególnych neuronach lub wartości wejściowe w przypadku pierwszej warstwy,
• literą \(w\) oznaczone są wartości oznaczające siłę poszczególnych połączeń (będziemy je nazywali wagami),
• górne indeksy mówią o numerze warstwy,
• dolne indeksy w oznaczeniach \(a\) numerują neurony w danej warstwie,
• pierwsze dolne indeksy w oznaczeniach \(w\) wskazują numery docelowych neuronów, natomiast drugie dolne indeksy wskazują numery neuronów, z których wychodzi dana synapsa.

Złożoność oznaczeń może na początku przerażać, ale nie warto się zniechęcać, ponieważ sama idea obliczeń nie jest tak skomplikowana. Cały mechanizm działania pojedynczego neuronu polega na wzięciu wartości z dochodzących do niego połączeń (synaps), wykonaniu na nich dwóch przekształceń, a następnie przekazaniu wyniku dalej do wszystkich neuronów w kolejnej warstwie.

Skupmy się na razie na pierwszym neuronie od góry w drugiej warstwie, nad którym znajduje się wartość \(a_1^2\). Symbol \(a_1^2\) to oznaczenie wartości, którą ten neuron oblicza w dwóch krokach. W pierwszym kroku obliczana jest pośrednia wartość
\begin{align}\label{eqn:z_formula}
z_1^2 = w_{1,1}^1 a_1^1 + w_{1,2}^1 a_2^1.
\end{align}
Warto zauważyć, że po lewej stronie górny indeks to \(2\), zaś po prawej zawsze \(1\). Oznacza to, że z wartości z poprzedniej warstwy obliczamy wartości dla kolejnej warstwy. Natomiast samo obliczenie polega na przemnożeniu wartości z poprzedniej warstwy przez siły odpowiednich połączeń (wagi) i zsumowanie obu wyników⁶.

W drugim kroku \(z_1^2\) przepuszczany jest przez tak zwaną funkcję aktywacji, której zadaniem jest redukcja szumu − pomniejszenie niewielkich wartości oraz powiększenie dużych wartości. W ten sposób zmniejsza się wpływ małych losowych wahań w danych, na których pracuje nasza sieć neuronowa, dzięki czemu sieć może skupić się na faktycznie istotnej informacji.

Do tego celu stosuje się tzw. funkcję sigmoidalną⁷:
\begin{align}\label{eqn:a_formula}
a_1^2 = \frac{1}{1 + \frac{1}{e^{z_1^2}}}.
\end{align}
We wzorze tym występuje druga po \(\pi\) najbardziej magiczna liczba matematyki − liczba \(e\)⁸. Jej wartość wynosi mniej więcej \(2{,}71\), jednak jest to liczba niewymierna i jej rozwinięcie jest nieskończone, podobnie zresztą jak liczby \(\pi\). Analogii jest więcej − tak samo jak liczba \(\pi\) pojawia się w bardzo wielu wzorach z geometrii i trygonometrii, tak liczba \(e\) w jeszcze bardziej magiczny sposób pojawia się niemal wszędzie w zaawansowanej matematyce.

Sam wzór wygląda na skomplikowany, warto więc zobaczyć wykres tej funkcji, który okazuje się zupełnie prosty.

Z tego wykresu od razu widać, że zgodnie z naszym oczekiwaniem funkcja sigmoidalna zmniejsza znaczenie małych wartości oraz zwiększa znaczenie dużych wartości. Warto także zwrócić uwagę, że funkcja sigmoidalna przyjmuje tylko wartości z przedziału \([0,1]\). Jest to tzw. normalizacja i stosuje się ją także do wartości wejściowych. Dzięki temu możliwe staje się porównywanie wielkości występujących w zupełnie różnych skalach, jak np. średniej ocen i zarobków.

Zupełnie analogicznie wygląda procedura obliczeń dla wszystkich pozostałych neuronów. Dla kompletności podajemy pełną postać wzorów w postaci macierzowej, która matematykom znacznie ułatwia zapisywanie skomplikowanych wyrażeń, a programistom pozwala zoptymalizować obliczenia. Dla drugiej warstwy mamy
\begin{align}
\begin{bmatrix}
z_1^2 \\
z_2^2 \\
z_3^2
\end{bmatrix}
&=
\begin{bmatrix}
w_{1,1}^1 & w_{2,1}^1 \\
w_{1,2}^1 & w_{2,2}^1 \\
w_{1,3}^1 & w_{2,3}^1
\end{bmatrix}
\begin{bmatrix}
a_1^1 \\
a_2^1
\end{bmatrix},
\qquad \qquad
\begin{bmatrix}
a_1^2 \\
a_2^2 \\
a_3^2
\end{bmatrix}
=
\begin{bmatrix}
\frac{1}{1 + \frac{1}{e^{z_1^2}}} \\
\frac{1}{1 + \frac{1}{e^{z_2^2}}} \\
\frac{1}{1 + \frac{1}{e^{z_3^2}}}
\end{bmatrix}
\end{align}
oraz dla trzeciej warstwy
\begin{align}
\begin{bmatrix}
a_1^3
\end{bmatrix}
&=
\begin{bmatrix}
w_{1,1}^2 & w_{1,2}^2 & w_{1,3}^2
\end{bmatrix}
\begin{bmatrix}
a_1^2 \\
a_2^2 \\
a_3^2
\end{bmatrix}
\end{align}

Z pierwszego z powyższych wzorów otrzymujemy np. wzór \eqref{eqn:z_formula} oraz analogiczne wzory dla \(z_2^2\) i \(z_3^2\). Rozumienie tego zapisu nie jest jednak w żaden sposób niezbędne, aby zrozumieć działanie sieci neuronowej. Niemniej warto taki zapis ujrzeć na własne oczy, aby zacząć się z nim oswajać. Zaś najpilniejsi czytelnicy mogą zweryfikować podany wzór, na przykład sprawdzając zasady mnożenia macierzy.

Całość obliczeń dla naszej sieci neuronowej przebiega następująco:

1. Na wejściu do sieci neuronowej, czyli jako wartości \(a_1^1\) oraz \(a_1^2\), podawane są średnia ocen oraz wysokość zarobków rodziców⁹.
2. Z pomocą wzorów analogicznych do \eqref{eqn:z_formula} obliczane są wartości \(z_1^2\), \(z_2^2\), \(z_3^2\), a następnie zgodnie ze wzorem \eqref{eqn:a_formula} wartości \(a_1^2\), \(a_2^2\), \(a_3^2\).
3. Analogicznie obliczana jest wartość \(z_1^3\), a następnie \(a_1^3\), czyli ostateczny wynik.

Na temat wykonywania obliczeń (czyli w naszym przypadku generowania prognoz) z pomocą sieci neuronowej to już wszystko, natomiast uważny czytelnik z pewnością cały czas zastanawiał się, czym są i skąd się biorą owe wagi wykorzystywane w naszej sieci neuronowej. W ten sposób dochodzimy do drugiego i ostatniego elementu związanego z sieciami neuronowymi − do ich uczenia.

Z reguły na początku wszystkie wagi dobiera się zupełnie losowo, jednak w taki sposób z pewnością nie otrzymamy dobrych prognoz. Aby nauczyć naszą sieć neuronową dobrze przewidywać przyszłe zarobki nastolatków na podstawie średniej ocen z matematyki oraz zarobków rodziców, potrzebujemy prawdziwych danych, na których będziemy mogli przeszkolić naszą sieć.

Wyobraźmy sobie, że mamy do dyspozycji dane na temat siedmiu osób, zebrane w poniższej tabeli¹⁰.

Imię	Średnia ocen z matematyki	Łączne zarobki rodziców	Rzeczywiste zarobki w wieku 30 lat
Andrzej	2,31	11400	3050
Maja	5,21	3850	2900
Piotr	3,45	7700	2950
Michał	3,72	4300	2400
Aleksandra	4,12	6200	3000
Zuzanna	3,13	3300	2100
Jakub	4,76	8800	3800

Łatwo zauważyć, że najlepiej być bogatym i mądrym, a najgorzej biednym i niezbyt rozgarniętym, jednak ustalenie rzeczywistej relacji na bazie surowych danych nie jest proste. Do tego celu przeszkolimy naszą sieć neuronową, tzn. w taki sposób ustalimy wagi, żeby prognoza wygenerowana przez sieć dla siedmiu osób z tabeli powyżej różniła się jak najmniej od ich rzeczywistych zarobków w wieku 30 lat.

Naturalnie możliwe byłoby ręczne dopasowanie wszystkich wag, ale byłoby to niezwykle żmudne zadanie, a dla większych sieci neuronowych zupełnie niewykonalne. Już nawet nasza, niewielka sieć neuronowa wymaga ustalenia 9 wag. Dlatego do ich wyznaczenia skorzystamy z potęgi matematyki¹¹.

Na początku wybierzemy zupełnie przypadkowe wagi i sprawdzimy, jaką prognozę otrzymujemy dla Andrzeja. Powiedzmy, że nasza sieć neuronowa dla średniej \(2{,}31\) i zarobków rodziców \(11400\) zł zwróciła \(2100\) zł. Jako błąd moglibyśmy przyjąć odległość rzeczywistych zarobków od tej kwoty, obliczoną jako wartość bezwzględną¹² ich różnicy
\begin{align*}
|2100 – 3050| = 950.
\end{align*}

Następnie chcielibyśmy tak zmienić wagi między drugą a trzecią warstwą, a następnie wagi między pierwszą a drugą warstwą, aby nieco ten błąd zmniejszyć. W kolejnym kroku natomiast, stosując te nowe wagi, obliczylibyśmy prognozę dla Mai, a następnie znów wyznaczylibyśmy błąd i ponownie staralibyśmy się zmienić wagi tak, aby ten błąd zmniejszyć. Taką procedurę powtórzylibyśmy dla każdej kolejnej osoby, otrzymując ostateczną wielkość wszystkich wag.

Pozostaje tylko pytanie, skąd mamy wiedzieć, jak zmieniać wagi w taki sposób, aby błąd się zmniejszał.

Aby rozwiązać to zagadnienie w pierwszym kroku matematycy zamieniają błąd dany wartością bezwzględną na tzw. błąd kwadratowy:
\begin{align*}
(2100 – 3050)^2 = 902500
\end{align*}
lub ogólniej
\begin{align*}
(y – \hat{y})^2,
\end{align*}
gdzie \(y\) to rzeczywista wartość zarobków, a \(\hat{y}\) to prognoza uzyskana z naszej sieci neuronowej. Taki sposób obliczania błędu wydaje się bardziej skomplikowany, jednak z punktu widzenia szukania kierunku zmiany wag jest on znacznie łatwiejszy do stosowania¹³.

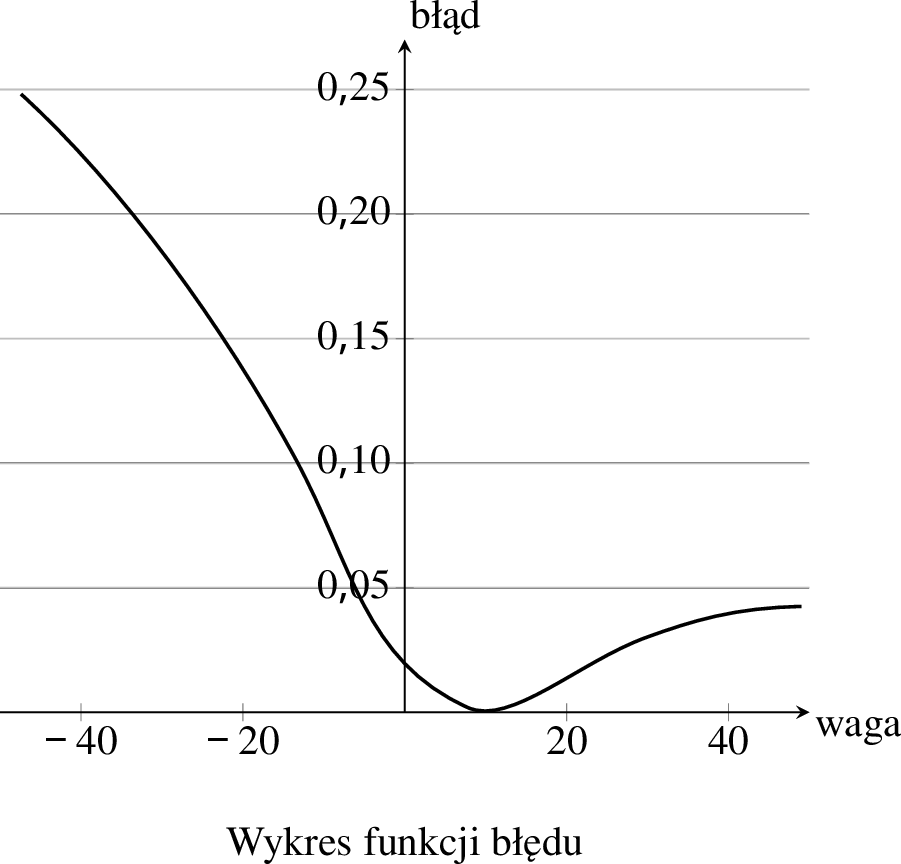
Zauważmy, że nasza sieć neuronowa będzie dawała różne prognozy dla różnych wartości wag. Tak samo różny będzie błąd, czyli wyrażenie \((y – \hat{y})^2\), gdy będziemy zmieniali wagi. Możemy więc narysować wykres, jak ten błąd zmienia się w zależności od wartości wag. Wyobraźmy sobie, że zależność błędu od jednej z wag wygląda jak na poniższym wykresie.

Jeśli przykładowo waga miała wartość \(w = -20\), to błąd wyniósł ok. \(0{,}2\). Z wykresu łatwo możemy stwierdzić, że najniższa wartość błędu (w istocie równa \(0\)) osiągnięta zostaje dla \(w = 10\). Z tego też powodu chcemy przesunąć wartość wagi \(w\) w stronę \(10\). Przesunięcie aż do samego minimum nie jest wskazane, ponieważ taka wartość wagi może nie być odpowiednia dla kolejnych osób, dla których będziemy generowali prognozy. Dlatego dla każdej osoby wykonujemy tylko małe przesunięcie wartości wagi w kierunku ujemnego (skierowanego w dół) nachylenia funkcji błędu. Taka procedura nazywana jest metodą gradientu prostego (gradient to inne określenie nachylenia).

Ponieważ tę procedurę musi wykonać komputer, potrzebujemy precyzyjnego matematycznego sposobu wyznaczania nachylenia. Idealnie do tego zadania nadaje się pojęcie pochodnej funkcji. Nie będziemy tutaj podawać pełnej matematycznej definicji, ponieważ dużo prościej ideę pochodnej można zrozumieć w sposób graficzny.

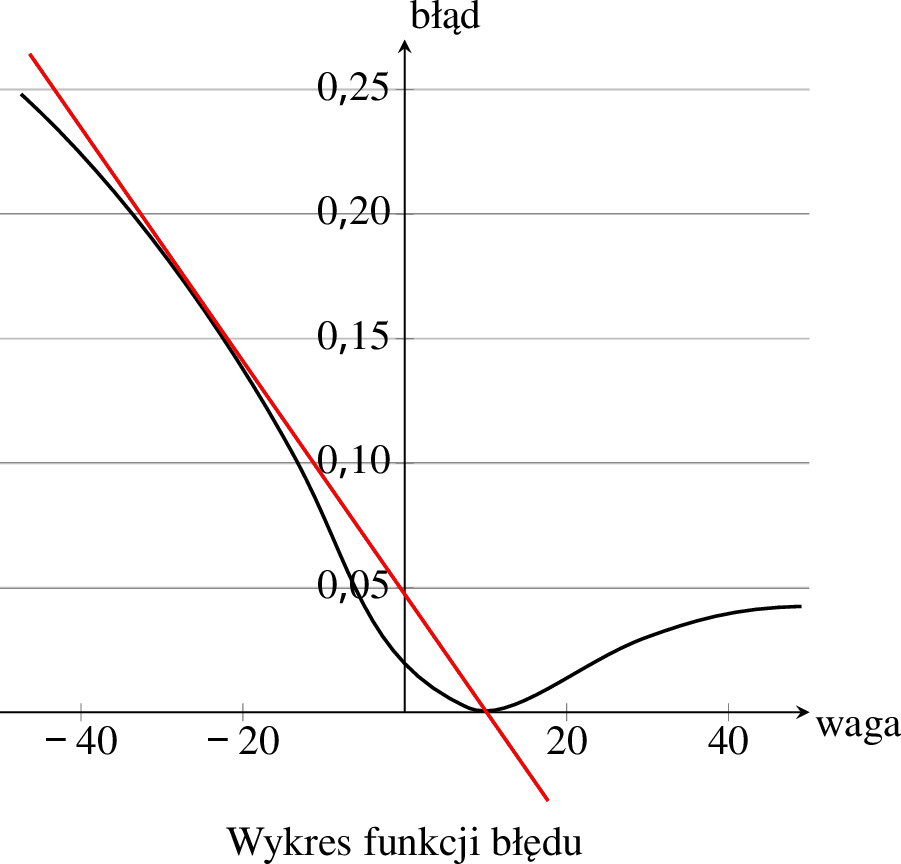
Na poniższym wykresie dodaliśmy prostą idealnie przylegającą¹⁴ do wykresu w miejscu odpowiadającym wartości wagi \(w = -20\).

Pochodna funkcji błędu w punkcie \(w = -20\) to dokładnie nachylenie tej prostej. W tym wypadku jest to nachylenie ujemne, ponieważ w okolicy \(w = -20\) wraz ze zwiększającą się wartością wagi wartość błędu spada.

Mając już wartość nachylenia, która w tym przypadku jest ujemna, wiemy już, że wartość wagi \(w\) musimy w tym przypadku przesunąć w prawo, czyli nieco zwiększyć.

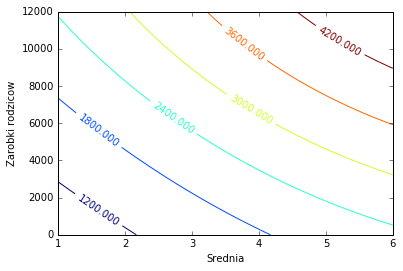
Po dokonaniu stosownych modyfikacji wszystkich wag dla wszystkich rozważanych osób otrzymujemy nauczoną sieć neuronową¹⁵. I taką sieć możemy zapytać o prognozę zarobków dla dowolnych kombinacji średniej ocen oraz zarobków rodziców. Otrzymane wyniki zestawiliśmy na dwóch poniższych wykresach.

Jako pierwszy prezentujemy wykres konturowy, który dla średniej ocen zaznaczonej na osi poziomej i zarobków rodziców zaznaczonych na osi pionowej prezentuje kształt krzywych, dla których prognozowane zarobki są jednakowe (o wartości podanej na danej krzywej).

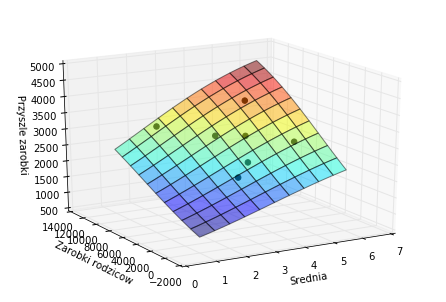
Drugi wykres prezentuje te same wyniki w trójwymiarze. Dodatkowo na wykresie umieszczone zostały czarne kropki symbolizujące siedem osób, na których danych uczyliśmy naszą sieć. Od razu można zauważyć, że sieć doskonale dopasowała się do tych danych.

Warto także własnoręcznie sprawdzić prognozę dla siebie samego. Pod tym linkiem przy pomocy WolframAlpha (narzędzia, z którym zdecydowanie warto się zaprzyjaźnić) i przybliżonego wzoru można to zrobić, podstawiając w miejsce \(y\) miesięczne dochody rodziców, a w miejsce \(x\) własną średnią ocen z matematyki.

Jakie wnioski płyną więc z wyników uzyskiwanych z naszej sieci neuronowej? Wychodzi na to, że zupełny tłumok mający bogatych rodziców może liczyć na takie same zarobki, jak bardzo dobry uczeń z biednej rodziny, zaś najlepiej jednocześnie być dobrym uczniem oraz dzieckiem bogatych rodziców. To raczej demotywujący wniosek. Nie zmienia to jednak faktu, że średnia ocen z matematyki ma bardzo duży wpływ na nasze przyszłe zarobki. Osoba z rodziny o średnich dochodach może w przyszłości liczyć na dwukrotnie wyższe dochody, jeśli zamiast średniej \(2{,}0\) ma średnią \(5{,}0\). Co równie istotne, rodziców się nie wybiera, a na nasze oceny mamy ogromny wpływ. Co zaś najważniejsze, nasza sieć neuronowa podaje jedynie prognozy najbardziej prawdopodobne ze statystycznego punktu widzenia. W rzeczywistości nawet osoba z bardzo biednej rodziny, wkładając mnóstwo pracy w swoją naukę i osiągając bardzo dobre wyniki, może ostatecznie trafić do Google albo SpaceX i zarabiać 20−30 tys. zł miesięcznie.

Epoka matematyki

Wiecie już teraz, jak działają filtry anty-spamowe oraz sieci neuronowe. To oczywiście nie wszystkie matematyczne metody stosowane przez gigantów z Doliny Krzemowej, czy szerzej współczesne firmy technologiczne, jednak statystyka bayesowska oraz sieci neuronowe to istotna część stosowanych technik.

Świat zmienia obecnie swoje oblicze w niezwykłym tempie. Niedługo samodzielne prowadzenie samochodu może być zakazane¹⁶, ponieważ sztuczna inteligencja będzie powodowała znacznie mniej wypadków. W ciągu najbliższych dziesięcioleci rozpoczniemy eksploatację minerałów z asteroid¹⁷ oraz eksplorację odległych księżyców, np. Tytana czy Europy¹⁸. I w tych misjach główną rolę odgrywać będą roboty, być może przywożąc nam później niezwykłe opowieści

− „Widziałem rzeczy, którym wy − ludzie − nie dalibyście wiary. Statki szturmowe w ogniu sunące ku ramionom Oriona. Oglądałem promienie kosmiczne błyszczące w ciemnościach blisko wrót Tannhausera.”¹⁹. Powoli też algorytmy i roboty zaczną wykonywać coraz więcej prac, od sprzątania, poprzez opiekę nad osobami starszymi, po wykonywanie analiz rynkowych, analizę danych czy nawet programowanie. Być może spełnią się wtedy prognozy stawiane w połowie XX wieku przez wielkiego ekonomistę Johna Maynarda Keynesa, że będziemy pracować jedynie po trzy godziny dziennie.

Ogromne zmiany technologiczne i społeczne są nieuniknione i ta nowa rzeczywistość tworzy się na naszych oczach. Dziś łatwiej niż kiedykolwiek można stać się Kolumbem swoich czasów, kształtującym obraz całego świata. Największe gwiazdy na świecie to Demis Hassabis czy Andrew Ng − matematycy pracujący nad sztuczną inteligencją, którzy już zarabiają więcej niż gwiazdy futbolu. Warto samemu zainteresować się matematyką, by stać się częścią tej niezwykłej przygody oraz współtwórcą nowej rzeczywistości i aby − przy okazji − trzymać rękę na pulsie, żeby władzy nad światem nie przejął Skynet²⁰.

Przypisy

1. Przybliżone metody rozwiązywania różnych problemów, dające nie optymalne, ale wystarczająco dobre odpowiedzi.
2. W 2014 roku DeepMind Technologies zostało kupione przez Google i obecnie nazywa się Google DeepMind.
3. AI od artificial intelligence, czyli sztuczna inteligencja.
4. Wybór matematyki jest zupełnie nieprzypadkowy, ponieważ zgodnie z prowadzonymi w Stanach Zjednoczonych badaniami to właśnie wyniki z matematyki mają największe znaczenie dla przyszłych zarobków.
5. Należy jednak dodać, że struktura i sposób działania tak dużych sieci są bardziej złożone niż dla przykładu podanego w tym artykule.
6. Zasada taka, jak przy obliczaniu średniej ważonej.
7. Inaczej nazywaną krzywą logistyczną
8. O liczbie \(e\) można poczytać na przykład w tym tekście − przy. red.
9. A dokładnie ich wartości znormalizowane.
10. Nie są to dane rzeczywiste, są jednak dobrane na podstawie badań wpływu średniej ocen z matematyki oraz zarobków rodziców na przyszłe zarobki nastolatków prowadzonych przez wiele lat w Stanach Zjednoczonych. Zakładamy, że dla Polski zależności nie będą aż tak odmienne.
11. Uważny Czytelnik zauważy być może, że Poznańska Fundacja Matematyczna realizuje przedsięwzięcie zatytułowane Potęga matematyki. Jak widać, nazwa projektu nie jest przypadkowa − przy. red.
12. Wartość bezwzględna jest odległością od zera danej liczby, przykładowo \(|5| = 5\), \(|-12| = 12\).
13. Dla zainteresowanych: wyrażenie kwadratowe jest różniczkowalne, a wartość bezwzględna nie, co znacząco przekłada się na łatwość minimalizowania błędu.
14. Mówiąc ściślej − styczną.
15. Oczywiście takich obliczeń nie wykonuje się ręcznie. Prezentowane w tym artykule wyniki zostały uzyskane przy pomocy sieci neuronowej napisanej w języku programowania Python, jednym z najczęściej wykorzystywanych w sztucznej inteligencji języków.
16. Jak np. w filmie „Ja, robot”
17. Już istnieją firmy, które mają na celu eksploatację asteroid, np. Deep Space Industries, czy Planetary Resources stworzona przez założyciela Google − Larry’ego Page’a, szefa Google − Erica Schmidta oraz reżysera Jamesa Camerona.
18. W ogromnym oceanie pod powierzchniowym lodem na Europie może istnieć życie.
19. Cytat z „Łowcy Androidów” Ridleya Scotta.
20. Superinteligencja z filmu „Terminator”.

---

Artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.