Własności liczb naturalnych nie przestają fascynować matematyków od najdawniejszych czasów. Własnościami liczb naturalnych zajmowali się starożytni matematycy, czego dowodem jest to, że Euklides poświęcił kilka tomów swojego dzieła liczbom. W Elementach pojawia się zasadnicze twierdzenie arytmetyki, które mówi:

ZASADNICZE TWIERDZENIE ARYTMETYKI
Każda liczba naturalna rozkłada się jednoznacznie, z dokładnością do kolejności czynników, na iloczyn liczb pierwszych.

Powyższe twierdzenie mówi nam, że liczby naturalne można zbudować z „atomów”, którymi są liczby pierwsze. Fakt ten pozwala czasami zredukować badany problem dotyczący liczb naturalnych do badania tylko liczb pierwszych.

W teorii węzłów najważniejszym problemem jest problem klasyfikacji węzłów. Problem ten jest niezwykle trudny, dlatego matematycy wymyślili sposób zredukowania tego problemu do pewnej podklasy węzłów. Sposób ten polega na przeniesieniu Zasadniczego Twierdzenia Arytmetyki do świata węzłów. Pierwszym krokiem jest wprowadzenie działania w zbiorze węzłów.

Niech $D_1$ będzie diagramem węzła położonym w półpłaszczyźnie $x < 0$ oraz niech $D_2$ będzie diagramem innego węzła, który leży w półpłaszczyźnie $x > 0$.

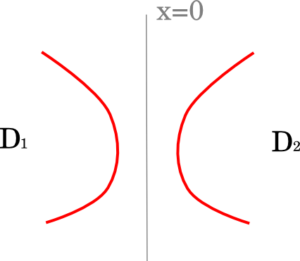
Następnie wybieramy po jednym punkcie z każdego diagramu i łączymy wybrane punkty krzywą, która nie przecina żadnego z diagramów poza punktami końcowymi.

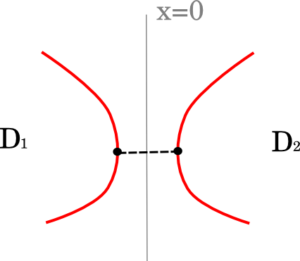
W kolejnym kroku pogrubiamy łączącą krzywą i otrzymujemy sumę dwóch węzłów, którą oznaczamy $D_1 \# D_2$.

Po zastosowaniu operacji sumy spójnej do dwóch trójlistników otrzymujemy następujący węzeł.

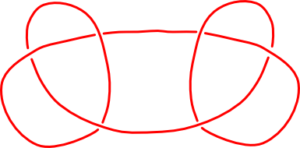
Suma dwóch węzłów jest dobrze określona, co oznacza, że diagramy, które powstaną przez powtórzenie powyższej procedury z innym wyborem punktów i krzywej będą równoważne.

Mnożenie liczb naturalnych jest działaniem łącznym, przemiennym oraz posiada element neutralny. W terminologii matematycznej powiedzielibyśmy, że zbiór liczb naturalnych z mnożeniem jest przemiennym monoidem. Okazuje się, że zbiór węzłów wraz z powyżej zdefiniowaną operacją jest monoidem.

ZADANIE. Sprawdź, że suma w zbiorze węzłów jest działaniem łącznym, tj. dla dowolnych $D_1$, $D_2$ i $D_3$ mamy $(D_1 \# D_2) \# D_3 = D_1 (D_2 \# D_3)$, przemiennym, tzn. $D_1 \# D_2 = D_2 \# D_1$, oraz, że węzeł trywilny $U$ jest elementem neutralnym, czyli $D_1 \# U = U \# D_1 = D_1$.