Co mają wspólnego użytkownicy Facebooka i osoby wspominane w Biblii? Na pierwszy rzut oka nic, a jednak… W tym artykule dyskutować będziemy o portalu Facebook z perspektywy matematyka, co stanie się inspiracją do wzmianki o grafach i ich własnościach. Niespodziewanie ta dyskusja doprowadzi nas do podobieństw między, na przykład, użytkownikami Facebooka a osobami wspominanymi w Biblii.

Facebook z punktu widzenia matematyka

Zacznijmy od pytania, jak najprościej matematycznie ująć strukturę Facebooka. Przedstawmy zarejestrowane osoby jako punkty (będziemy je nazywać później wierzchołkami). Jeśli użytkownicy Facebooka są znajomymi, to odpowiadające im punkty połączmy kreską (owe kreski będziemy nazywać krawędziami). Jeśli uwzględnilibyśmy wszystkich użytkowników Facebooka, to w ten sposób powstałby ogromny obrazek (obrazek tak zwanego grafu). Takie struktury, które można opisać za pomocą grafu nazywamy sieciami. Pod koniec tego artykułu wymienimy jeszcze kilku innych interesujących przykładach sieci.

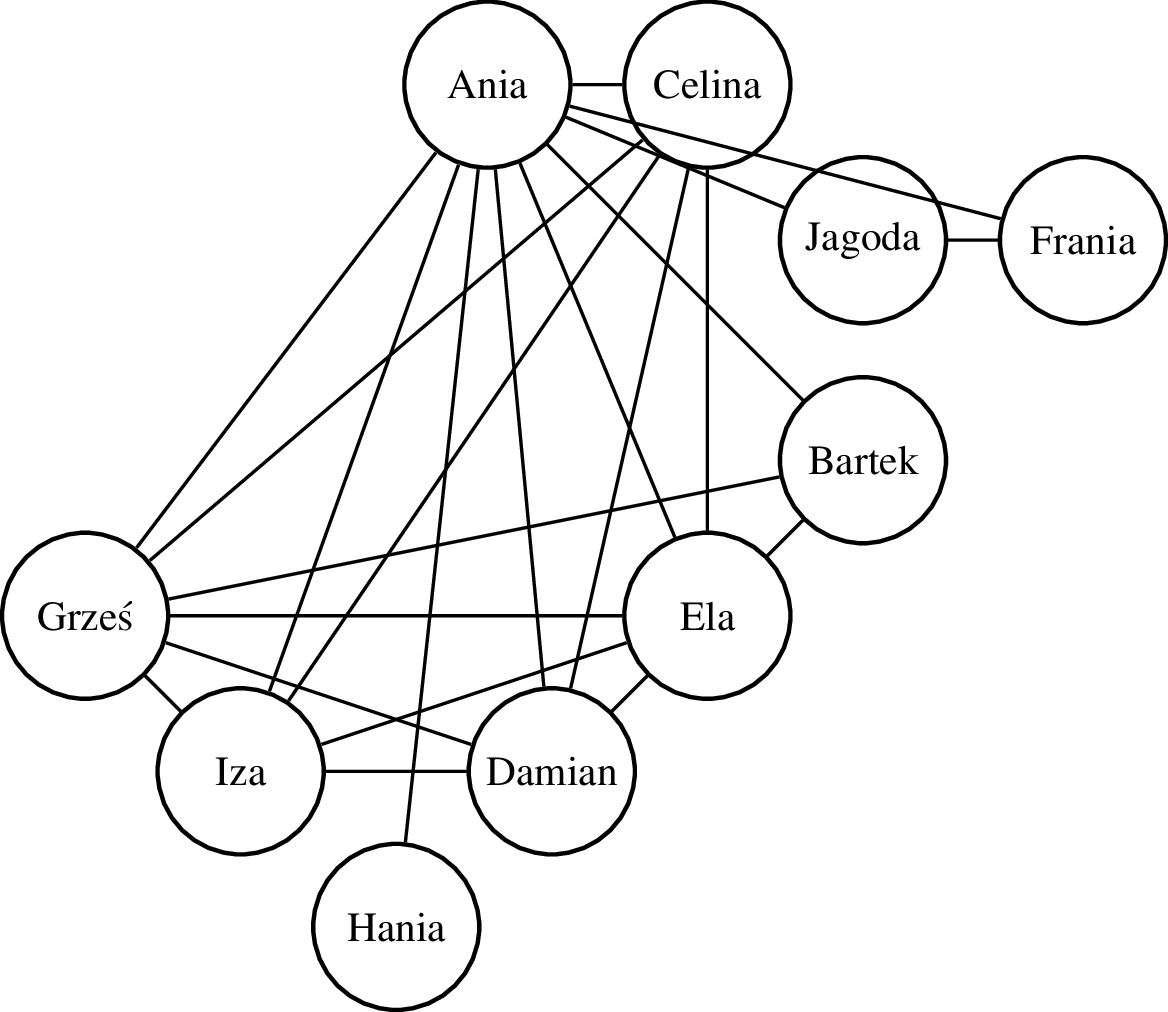
Zaczniemy jednak od grafu Facebooka. Przykładowy fragment tego grafu, przedstawiający znajomych pewnej Ani, prezentujemy na poniższej ilustracji.

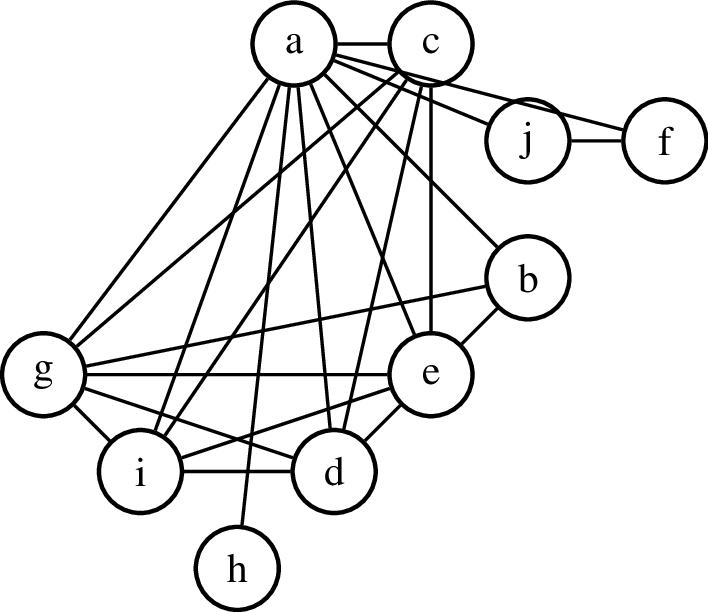
Dla wygody możemy ten obrazek narysować bardziej schematycznie.

Na obrazku są wierzchołki (punkty — dla wygody przedstawione jako kółka):
\[
a,b,c,d,e,f,g,h,i,j
\]
oraz kreski je łączące, czyli krawędzie (dla uproszczenia krawędzie opisujemy jako pary wierzchołków):
\begin{gather*}
\{a,b\}, \{a,c\}, \{a,d\}, \{a,e\}, \{a,f\}, \{a,g\}, \{a,h\}, \{a,i\}, \{a,j\},\\
\{c,d\}, \{c,e\}, \{c,g\}, \{c,i\}, \{d,e\}, \{d,g\}, \{d, i\}, \{e,g\}, \{e,i\}, \{g,i\}, \\
\{b,e\}, \{b,g\}, \{j,f\}.
\end{gather*}

Jesteśmy teraz gotowi na to, żeby zdefiniować pojęcie grafu. Grafem nazywać będziemy parę \((V,E)\), gdzie \(V\) jest zbiorem wierzchołków, a \(E\) zbiorem nieuporządkowanych par wierzchołków zwanych krawędziami. Zwykle graf oznaczać będziemy literką \(G\). W przypadku grafu z powyższych ilustracji mamy
\begin{align*}
V=&\{a,b,c,d,e,f,g,h,i,j\};\\
E=&\{
\{a,b\}, \{a,c\}, \{a,d\}, \{a,e\}, \{a,f\}, \{a,g\}, \{a,h\}, \{a,i\}, \{a,j\},\\
&\{c,d\}, \{c,e\}, \{c,g\}, \{c,i\}, \{d,e\}, \{d,g\}, \{d, i\}, \{e,g\}, \{e,i\}, \{g,i\}, \\
&\{b,e\}, \{b,g\}, \{j,f\}
\}.
\end{align*}
Matematykowi potrzebny jest taki formalizm, ale czytelnik — dla wygody — może poprzestać na myśleniu o punktach i łączących je kreskach.

Obiecaliśmy opowiedzieć o własnościach Facebooka, a dokładniej o własnościach jego grafu. Skupimy się na trzech z tych własności: współczynniku skupienia (ang. clustering coefficient), średnicy i stopniu wierzchołków. Zanim jednak zaczniemy opowieść, zrobimy kilka ogólnych uwag dotyczących grafów w ogóle, a w szczególności grafu Facebooka.

Podkreślmy, że graf Facebooka jest ogromny (w drugim kwartale 2016 roku około 1,71 miliards użytkowników korzystało z Facebooka co najmniej raz w miesiącu). Zaraz się przekonamy, że mimo wielkiej liczby wierzchołków, graf Facebooka zawiera w porównaniu do swojej wielkości niewiele krawędzi. Każdy z czytelników wie, ilu ma znajomych na Facebooku i zdaje sobie sprawę, że nawet największe ,,facebookowe świry” nie są w stanie mieć znaczącej (w porównaniu z liczbą wszystkich uczestników Facebooka) ich liczby. Dla wygody będziemy zakładać, że średnia liczba znajomych wynosi¹ 155. w 2016 roku średnia liczba przyjaciół wynosiła około 155. Co z tego wynika dla grafu? W dowolnym grafie o \(n\) (jeśli ktoś obawia się \(n\), niech myśli teraz i w pozostałej części artykułu o Facebooku 1,71 miliarda) wierzchołkach z wierzchołka może wyjść co najwyżej \(n-1\) krawędzi, czyli w sumie krawędzi może być nawet \(\frac{n(n-1)}{2}\). Jak uzyskujemy ten wynik? Liczymy po kolei ile krawędzi wychodzi z każdego wierzchołka i sumujemy otrzymane liczby. Teraz zauważamy, że każdą krawędź liczyliśmy dwa razy, zatem musimy wynik podzielić przez dwa. Jeśli oznaczymy przez \(n\) liczbę użytkowników Facebooka i przez \(d\) średnią liczbę znajomych użytkownika Facebooka (jeśli ktoś obawia się \(d\), to teraz i w dalszej części artykułu niech myśli o 155), to w grafie Facebooka mamy \(\frac{nd}{2}\) krawędzi (znów liczymy po kolei ile krawędzi wychodzi z każdego wierzchołka i sumujemy, a następnie dzielimy przez dwa, bo każda krawędź została policzona dwukrotnie). Skoro \(d\) jest duuużo mniejsze od \(n\) to \(\frac{nd}{2}\) jest duuużo mniejsze niż \(\frac{n(n-1)}{2}\), a co za tym idzie graf Facebooka jest bardzo rzadki².

W dodatku graf Facebooka ma bardzo specyficzną strukturę. Jeśli krawędzie byłyby w nim rozłożone równomiernie, to prawie równo prawdopodobne byłoby, że znamy Kasię z Polski lub Kate z USA czy Catherine z Francji. Tak jednak nie jest. Jakie cechy grafu się z tym wiążą, dowiemy się niebawem.

Znajomy znajomego, czyli współczynnik skupienia i kliki

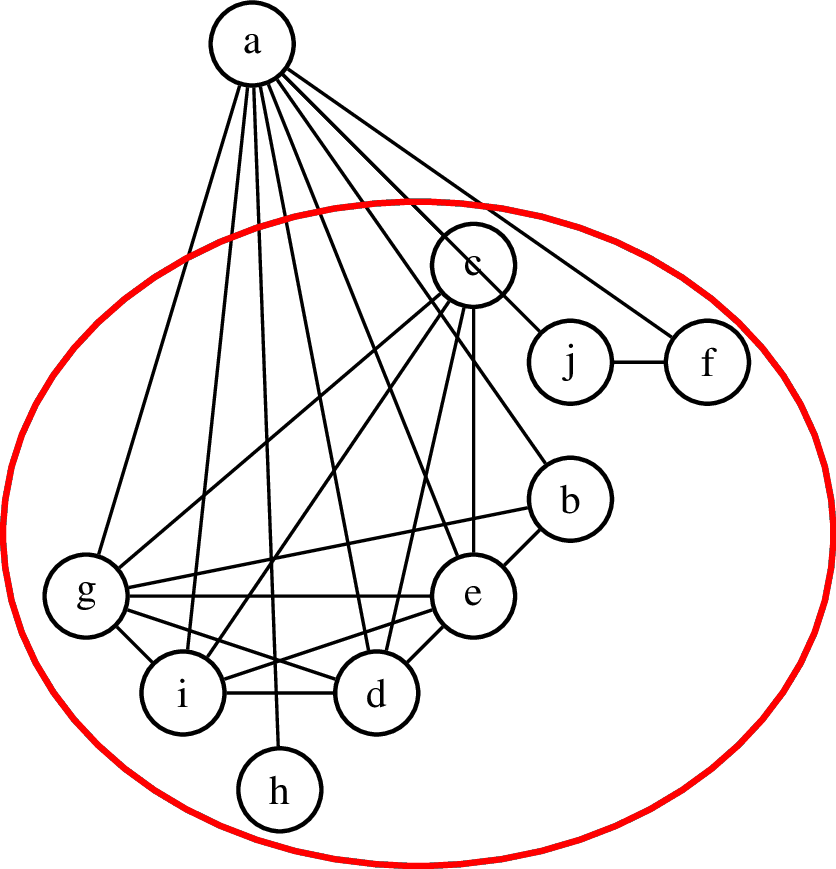
Spójrzmy teraz na graf Facebooka lokalnie, czyli tak jakby przez szkło powiększające na jego fragment. Wspomnieliśmy, że globalnie graf Facebooka jest bardzo rzadki, ale lokalnie może on zawierać bardzo gęste skupiska krawędzi. Zerknijmy jeszcze raz na znajomych Ani. Ania ma 9 znajomych (formalnie w teorii grafów ci znajomi to sąsiedzi wierzchołka \(a\) w grafie), ale wśród nich krawędzie nie są rozłożone równomiernie. Istotne dla struktury tego grafu jest to, że Ania ma 5 znajomych (\(c,d,e,g,i\)), którzy znają się nawzajem (są parami połączeni krawędziami). Taki graf, w którym występują wszystkie możliwe krawędzie nazywamy kliką³. Często znajomy znajomego jest naszym znajomym, więc w grafie Facebooka będzie dużo takich klik. Mówiąc prościej, jeśli Ania zna Grzesia i Celinę, to jest duża szansa na to, że Grześ z Celiną też się znają. Jaki jednak sposób znaleźli matematycy, aby ,,zmierzyć” jak duża jest szansa na to, że dwóch znajomych pewnego użytkownika Facebooka jest znajomymi? Miarą tej zależności jest tak zwany współczynnik skupienia.

Współczynnik skupienia danego wierzchołka w grafie (w naszym przypadku współczynnik skupienia Ani w grafie Facebooka) jest równy liczbie krawędzi łączących pary sąsiadów tego wierzchołka podzielonej przez liczbę par sąsiadów (czyli liczbę wszystkich możliwych połączeń między parami sąsiadów).

W przypadku Ani współczynnik skupienia wierzchołka \(a\) w grafie Facebooka jest równy
\[
C(a)=\frac{14}{\frac{9\cdot 8}{2}}=\frac{7}{18}.
\]
Współczynnik skupienia całego grafu to średnia arytmetyczna ze współczynników skupienia wszystkich wierzchołków⁴. Tak zdefiniowany współczynnik skupienia jest miarą szansy na to, że znajomy znajomego jest naszym znajomym. W sieciach społecznościowych, nawet gdy mamy mało znajomych, wielu z tych znajomych zna się między sobą. Dlatego można się spodziewać, że współczynnik skupienia sieci Facebooka jest ,,duży”. Za chwilę wytłumaczymy, co mamy na myśli.

Zastanówmy się, ile wynosiłby w przybliżeniu ten współczynnik, gdyby krawędzie były ,,równomiernie” rozłożone w całym grafie. Załóżmy, że mamy graf o \(n\) wierzchołkach (zakładamy, że \(n\) jest bardzo duże, np. 1,71 miliarda), w którym każdy wierzchołek ma około \(d\) sąsiadów (zakładamy, że \(d\) jest małe, np. 155). Jeśli wybierzemy losową parę wierzchołków, to szansa, że łączy je krawędź wynosi około \(d/n\). Zatem, jeśli wierzchołek ma \(d\) sąsiadów, to wśród nich jest zazwyczaj około \( \frac{d(d-1)}{2}\cdot \frac{d}{n}\) krawędzi. To daje nam współczynnik skupienia \(d/n\) (około 155 podzielone przez 1,71 miliarda, czyli mniej niż 0,0000000001). Z drugiej strony zgodnie z danymi z 2009 roku⁵ współczynnik skupienia grafu Facebooka znajduje się w okolicach 0,13. Z tego wynika, że współczynnik skupienia grafu Facebooka jest bardzo duży (\(\approx\) 0,13) w stosunku do gęstości grafu (\(\approx\) 0,0000000001).

Świat jest mały, czyli średnie odległości

W tym rozdziale skupimy się na pytaniu, czy korzystając z Facebooka możemy przesłać wiadomość od dowolnego użytkownika do dowolnego użytkownika korzystając tylko z połączeń ze znajomymi. Wyobraźmy sobie, że Ania korzystając z Facebooka chciałaby przesłać wiadomość do ustalonej Kate z USA. Chciałby jednak korzystać z pewnych połączeń, czyli może tę wiadomość przesłać swojemu znajomemu, ów znajomy swojemu znajomemu itd. Czy uda się to Ani, zakładając, że Ania zna strukturę całego grafu Facebooka? W dodatku istotne jest pytanie, ilu innych użytkowników Facebooka odwiedzi ta wiadomość po drodze? Jest to pytanie o tak zwany poziom oddzielenia (ang. degree o separation) sieci Facebook.

Przetłumaczymy pytanie na język teorii grafów. Ania poszukuje ścieżki łączącej wierzchołek Ani z wierzchołkiem Kate. Przez ścieżkę rozumiemy ciąg wierzchołków, w którym kolejne (to znaczy występujące jeden za drugim w ciągu) wierzchołki są połączone krawędzią w grafie. W grafie Ani przykładem ścieżki jest \((f,j,a,h)\). Ania chciałaby, aby ścieżka między nią a Kate była jak najkrótsza, czyli jej długość (liczba krawędzi) była jak najmniejsza. Na przykład długość ścieżki \((f,j,a,h)\) wynosi trzy natomiast najkrótsza ścieżka z \(f\) do \(h\) to \((f,a,h)\) i jej długość wynosi dwa. Długość takiej najkrótszej ścieżki od Ani do Kate, to odległość wierzchołka Ani od wierzchołka Kate w grafie Facebooka. Zatem ostatecznie pytanie o poziom oddzielenia w języku teorii grafów brzmi:

Czy istnieje ścieżka między wierzchołkiem Ani a wierzchołkiem Kate i — jeśli ścieżka istnieje — to jaka jest odległość między wierzchołkiem Ani a wierzchołkiem Kate.

Odpowiemy na te pytania opierając się na danych statystycznych. Według danych z 2012 roku⁶ w grafie Facebooka można było znaleźć zbiór wierzchołków składający się z około 90% wszystkich wierzchołków o tej własności, że dowolne dwa wierzchołki w tym zbiorze są połączone ścieżką. Z tego wynika, że jest duża szansa na powodzenie przesłania informacji od Ani do Kate. Drugie pytanie dotyczy długości ścieżki przesyłu tej informacji. Okazuje się, że według tych samych danych z 2012 roku, średnia odległość między dwoma połączonymi ścieżką użytkownikami Facebooka wynosi około 4,7. Dane co do ograniczeń górnych na długość tej ścieżki nie są już tak jednoznacznie, ale jest bardzo prawdopodobne, że w prawie wszystkich przypadkach ta wartość nie przekracza \(50\). Wartości 4,7 a nawet 50 są znacząco mniejsze od rozmiaru całej sieci (1,71 miliards). Własność, która mówi, że w rzadkiej sieci można przesłać informację wykorzystując krótką ścieżkę, nazywa się fenomenem małego świata (ang. the small world phenomenon). Przy okazji, ile razy w waszym życiu mieliście okazję powiedzieć, że ,,świat jest mały”?

Ilu mamy znajomych, czyli stopnie wierzchołków

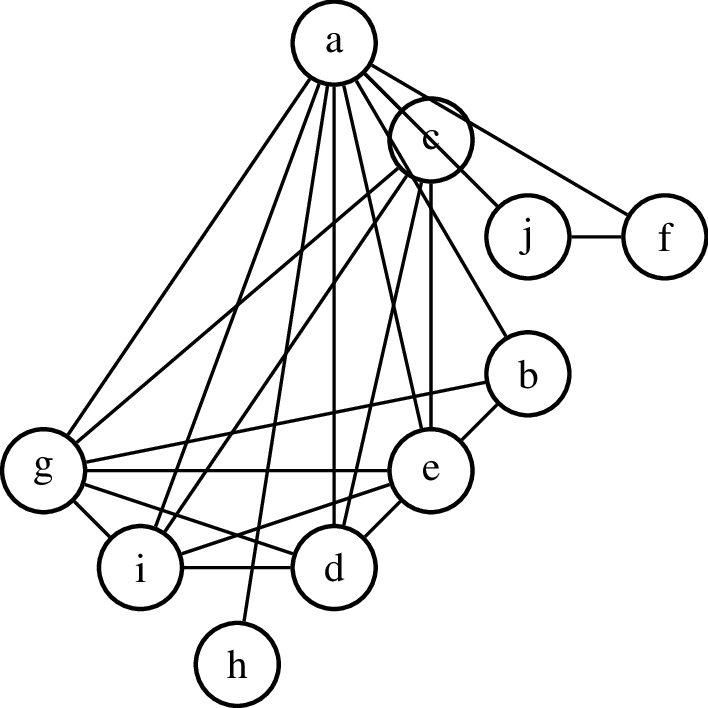
Spójrzmy przez chwilę znów na graf Ani.

W tym grafie wierzchołek \(a\) (Ania) jest połączony z dziewięcioma innymi wierzchołkami. W teorii grafów mówimy, że wierzchołek \(a\) ma stopień 9. Ile wynoszą stopnie wszystkich wierzchołków w tym grafie? Wymieńmy je rozpatrując wierzchołki w kolejności alfabetycznej:
\[
9, 3, 5, 5, 6, 2, 6, 1, 5, 2.
\]
A teraz ustawmy je w kolejności nierosnącej
\[
9, 6, 6, 5, 5, 5, 3, 2, 2, 1.
\]
Taki ciąg nazywamy ciągiem stopni grafu. Wyobraźmy sobie teraz ciąg stopni grafu Facebooka i spytajmy się o jego globalne własności. Najprostsze pytanie byłoby: jaka część z elementów tego ciągu jest większa niż \(k\), dla ustalonego naturalnego \(k\)? Okazuje się, że istnieje taka stała \(\alpha\), że dla większych wartości \(k\) liczba wierzchołków o stopniu co najmniej \(k\) (liczba elementów w ciągu, które mają wartość co najmniej \(k\)) jest proporcjonalna do \(1/k^{\alpha}\). Dla ciągów stopni o tej własności mówimy, że spełniają prawo potęgowe (ang. power law).

To o co w końcu chodzi z tą Biblią?

Czytelnik może czuć się zniecierpliwiony, bo opowieść miała być o związku Facebooka z Biblią a my tylko rozmawiamy o jakimś grafie i jego własnościach. Zaręczamy, że cierpliwość popłaca. Podsumujmy:

Użytkownicy Facebooka i sieć znajomości między nimi wyznaczają graf o pewnych szczególnych własnościach. Graf ten jest rzadki, ma duży w porównaniu z gęstością krawędzi współczynnik skupienia, zachodzi w nim fenomen małego świata, a ciąg stopni wierzchołków spełnia prawo potęgowe.

Spójrzmy teraz na inne duże sieci i zapytajmy, czy mają one podobne własności. Przykładem może być sieć, w której wierzchołki to biblijne imiona, które łączymy krawędzią, jeśli występują w jednym wersie w konkretnym wydaniu Biblii. Okazuje się, że ta sieć posiada bardzo podobne własności, co Facebook. Zmienia się jedynie liczba wierzchołków w sieci, wartość współczynnika skupienia (choć nadal jest duży w porównaniu z gęstością), średnie odległości między wierzchołkami (choć nadal są małe w porównaniu z wielkością) oraz wykładnik potęgowy \(\alpha\) dla ciągu stopni.

Dłuższe badania nad własnościami sieci pokazują, że Facebook i sieć biblijnych imion nie są osamotnione. Nie musimy sięgać daleko. Wystarczy wziąć: sieć stron internetowych (z ich linkami), sieć routerów internetowych (z ich połączeniami), sieć współwystępowania autorów w filmach, sieć cytowań prac naukowych i wiele, wiele innych. Wszystkie te sieci należą do przeogromnej rodziny sieci złożonych (ang. complex networks) i to o tych sieciach jest ten artykuł.

I co tutaj mają do roboty matematycy?

Wiemy już, że istnieje na świecie wielka rodzina sieci, które mają bardzo szczególne własności. Świadczą o tym zebrane dane statystyczne. Teraz możemy zapytać, co ciekawego może z tym zrobić matematyk? Nasuwa się kilka naturalnych pytań.

• Dlaczego one mają takie a nie inne własności?
• Czy komputer możne wygenerować sieć (graf) o podobnych własnościach korzystając z jakiegoś algorytmu? Jak ten algorytm mógłby wyglądać?
• Jeśli chcemy zastosować pewien algorytm na tej sieci, czy będzie on dobrze działać? Jak to sprawdzić?

Wszystkie te pytania sprowadzają się do jednego matematycznego pytania: w jaki sposób sztucznie wyprodukować graf o własnościach sieci złożonej. Odpowiedzią na to pytanie są modele matematyczne sieci zwane grafami losowymi. To jednak jest temat na kolejną, niezwykle ciekawą, opowieść.

Ciekawe linki

W tym artykule podajemy wiele wartości dotyczących Facebooka, o których wspominamy, że nie są one pewne. Jest tak dlatego, że zbadanie całej sieci Facebooka jest niemożliwe ze względu na jej rozmiar. Większość tych danych wynika z badań statystycznych małych wyrywków Facebooka. W dodatku Facebook regularnie się rozwija, więc dane sprzed kilku lat (a nawet kilku miesięcy) są już nieaktualne. Podajemy jednak te wartości, aby uzmysłowić czytelnikowi rząd wielkości o jakich mówimy.

Swój fragment Facebooka można zanalizować tutaj.

O imionach w Biblii można poczytać tutaj.

Ciekawe zestawienie różnych sieci z ich własnościami można znaleźć tutaj.

Niektóre dostępne bazy danych dotyczące sieci można znaleźć między innymi tutaj.

Przypisy

1. W przypadku średniej liczby przyjaciół nie było łatwo znaleźć aktualne dane, na których można polegać. Według Pew Research Center w 2013 roku ta liczba to około 338, a według innych danych 155.
2. Dodajmy, że stosunek liczby krawędzi do największej możliwej liczby krawędzi w grafie nazywamy gęstością grafu.
3. Ciekawostką jest, że zgodnie z definicją słownika języka polskiego PWN klika to ,,grupa osób wzajemnie się popierających i dążących wspólnie do osiągnięcia własnych korzyści wbrew interesowi społecznemu”
4. Istnieją inne definicje współczynnika skupienia. Na przykład współczynnik skupienia całego grafu może być zdefiniowany jako potrojona liczba trójkątów w grafie, podzielona przez liczbę trójek \(v_1,v_2,v_3\) takich wierzchołków, że zarówno \(\{v_1,v_2\}\) jak i \(\{v_2,v_3\}\) jest krawędzią. W dużych grafach (sieciach) wartości otrzymane po zastosowaniu dowolnej ze znanych definicji są przybliżone.
5. Bimal Viswanath, Alan Mislove, Meeyoung Cha, Krishna P. Gummadi, On the Evolution of User Interaction in Facebook, Proceedings of the 2nd ACM SIGCOMM Workshop on Social Networks (WOSN’09), Barcelona (August, 2009).
6. Lars Backstrom, Paolo Boldi, Marco Rosa, Johan Ugander, Sebastiano Vigna, Four Degrees of Separation, Proceedings of the 4th Annual ACM Web Science Conference, WebSci ’12, 2012 (Evanston, Illinois), 33–42.

---

Artykuł został sfinansowany dzięki wsparciu pozyskanemu przez Poznańską Fundację Matematyczną od Miasta Poznań na realizację projektu ,,Potęga matematyki''.